考虑温度等多因素影响的拱桥吊杆张力识别*

2020-12-08燕朋朋

振动、测试与诊断 2020年5期

何容，燕朋朋，何伟，陈淮

(1.华北水利水电大学土木与交通学院郑州，450045) (2.郑州大学土木工程学院郑州，450001)

引言

吊杆作为中、下承式拱桥关键的受力构件，其张力变化与分配情况不仅反映了桥梁整体受力状态，而且与桥梁运营期安全、健康状态密切相关[1]。因此，精确识别吊杆的张力信息对确定全桥的健康状况至关重要[2]。

目前，振动频率法作为吊杆张力测试常用方法，具有简便、实用性强等优点，适用于各类吊杆，其测试精度与吊杆边界条件密切相关。为了提高吊杆张力测试精度，国内外学者多数针对吊杆张力识别方法以及吊杆边界条件进行了广泛研究。在识别方法方面，Park等[3]基于有限元模型的反分析和系统辨识方法计算吊杆张力，以提升基于弦振动理论和线性回归方法的可靠性。Kim等[4]利用数字图像处理技术对吊索的张力进行非接触测量，提高了吊索的动态响应和模态频率的分辨率。孙传智等[5]基于响应面法优化拱桥吊杆内力，为拱桥的设计和施工控制提供指导。文献[6]利用摄动技术考虑了吊索静态变形以提高吊索张力计算精度。在吊杆边界条件方面，何容等[7]考虑了吊索复合边界条件，基于能量法给出了吊索张力计算公式。张戎令等[8]考虑了吊杆抗弯刚度、转动惯量和剪切变形耦合影响，根据吊杆振动过程中动平衡状态给出了吊杆振动频率与张力计算关系式。唐盛华等[9]通过两端固结梁和两端铰接梁的频率特征方程，建立了形式简单的索力计算公式。单德山等[10]研究了减震器刚度对吊杆张力的影响，建立了吊杆张力与振动频率复杂关系式，利用牛顿插值法识别施工阶段吊杆张力。周强等[11]基于部件模态综合理论，建立了拉索-黏滞阻尼器系统在考虑拉索抗弯刚度和垂度时系统非线性振动模型，研究了不同边界条件下拉索抗弯刚度对系统一阶模态阻尼比的影响。此外，文献[12-14]研究了温度变化对吊杆张力测定的影响，结果显示温度变化将导致吊杆结构几何形态和内力发生变化。纵观国内外已有成果，大部分研究仅针对吊杆简单边界条件(固接或铰接)开展的，没有同时考虑吊杆复杂边界条件下弹性支撑、转动约束、黏性护套与附加质量等因素的影响，不能完全反映吊杆实际情况。

为了更精确地测定吊杆张力，综合考虑了吊杆抗弯刚度、长度、减振垫、附加质量、弹性支承、环境温度和黏性护套等多因素的影响，建立了拱桥吊杆张力计算模型，推导了复杂边界条件下吊杆张力与横向振动频率解析表达式。为便于工程应用，通过边界影响系数法给出了吊杆张力实用表达式，并进行了实例验证，分析了各表达式计算精度、应用特点及差异，为吊杆张力测定提供参考。

1 复杂边界条件下吊杆张力解析表达式

考虑抗弯刚度、长度、减振垫、附加质量、弹性支承、黏性护套、环境温度影响时，吊杆张力计算模型如图1所示。图中：F为吊杆张力；Ma和Mb分别为拱肋与系杆梁的等效质量；Ha和Hb分别为拱肋与系杆梁对吊杆横向等效刚度；H1和H2分别为拱肋与系杆梁对吊杆等效转动刚度；H3和H4分别为拱肋与系杆梁中减振垫对吊杆横向等效刚度；L为吊杆长度；EI为吊杆抗弯刚度；m为吊杆单位长度质量。

图1 吊杆张力计算模型Fig.1 The calculation model of hanger tension

考虑吊杆外部高密度聚乙烯护套的影响(图2)，并假定吊杆张力沿杆长方向不变，且护套与吊杆同步振动。在线弹性范围内，吊杆实际抗弯刚度EI与拉伸(压缩)刚度EA可分别表示为

(1)

其中：E1I1为钢绞线抗弯刚度；E2I2为黏性护套抗弯刚度；E1A1钢绞线拉伸(压缩)刚度；E2A2为黏性护套拉伸(压缩)刚度。其具体取值可参考国家标准《斜拉桥热挤聚乙烯高强钢丝拉索技术条件》(GB/T 18365-2001)。

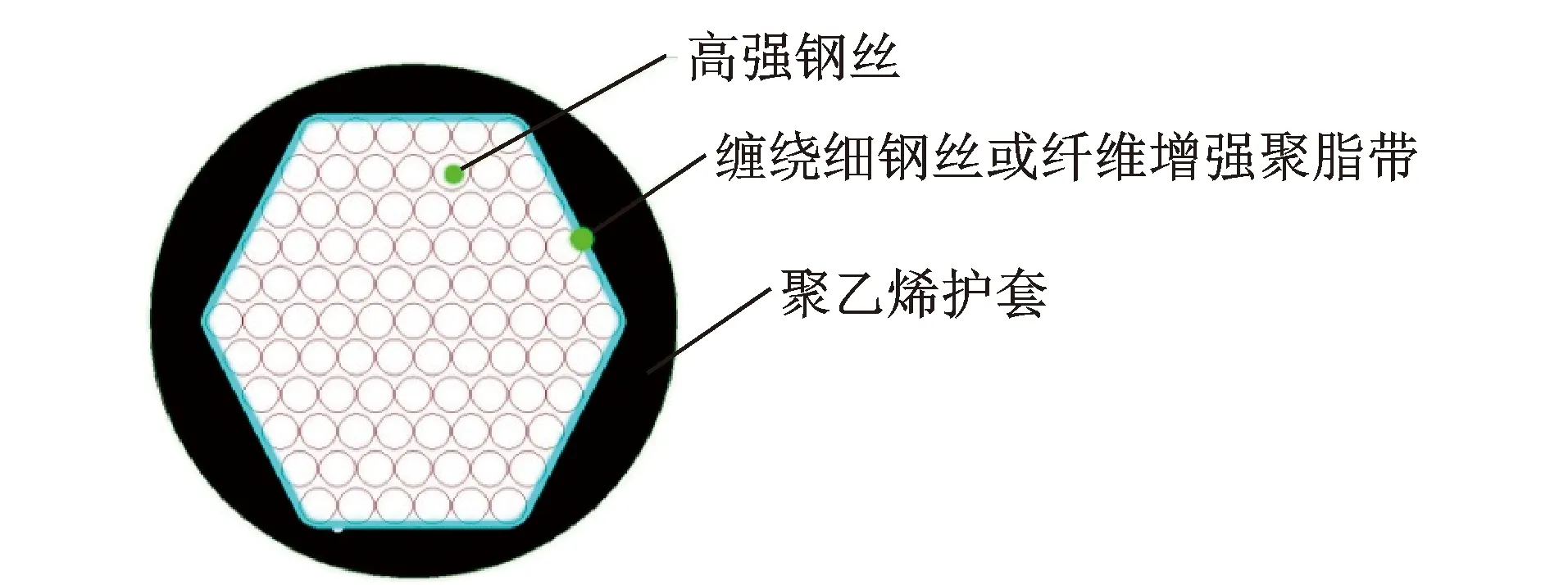
图2 吊杆断面结构示意图Fig.2 Schematic diagram of hanger section structure

忽略温度场梯度变化，由环境温度变化引起的吊杆张力变化FN为

FN=-EAμ(T-T0)

(2)

其中：μ为吊杆材料热膨胀系数；T0为吊杆张拉完成时的环境温度；T为当前环境温度。

为研究方便，可将拱肋或系杆梁对吊杆的轴向等效刚度与减振垫对吊杆的轴向等效刚度进行叠加。令Ka和Kb分别为拱肋、系杆梁与减振垫对吊杆横向等效刚度，则：Ka=Ha+H1，Kb=Hb+H2。由于减振垫与拱肋或系杆梁端部距离较近，可认为减振垫位于拱肋或系杆梁的端部，此时吊杆计算长度为L。

由Euler-Bernoulli梁理论，吊杆振动微分方程为

(3)

V(x,t)为吊杆横向位移函数, 可表示为

V(x,t)=φ(x)Z(t)

(4)

其中：Z(t)和φ(x)分别为吊杆的广义振幅坐标和振型函数。

φ(x)=C1cos(αx)+C2sin(αx)+

C3cosh(βx)+C4sinh(βx)

(5)

其中

(6)

(7)

C1,C2,C3,C4为待定系数，可根据吊杆边界条件确定。

根据吊杆端部作用力和力矩平衡，可得吊杆边界条件方程组为

EIφ″(0)+H3φ′(0)=0

(8)

EIφ‴(0)+Haφ(0)-Maω2φ(0)-Fφ′(0)=0

(9)

EIφ″(L)+H4φ′(L)=0

(10)

EIφ‴(L)-Hbφ(L)+Mbω2φ(L)+Fφ′(L)=0

(11)

将吊杆振型函数式(5)代入上述边界条件，构成以待定系数C1,C2,C3,C4为基本未知量的方程组，即

(12)

其中

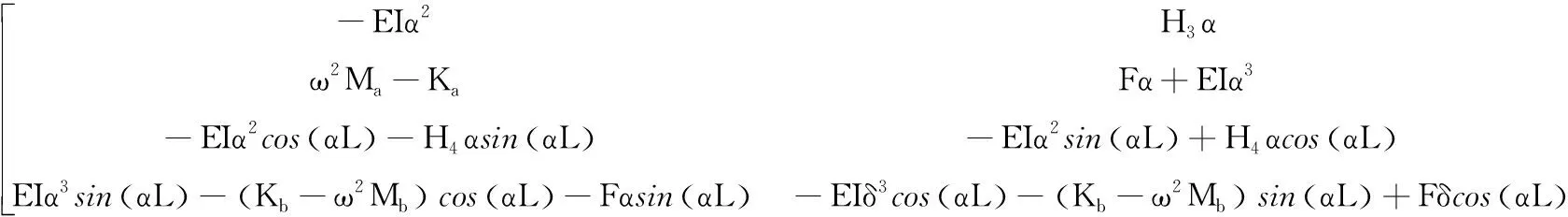
为使式(12)有非零解，则其待定系数C1,C2,C3,C4所构成的矩阵行列式值应为0，即

|R|=0

(13)

式(13)即为考虑抗弯刚度、长度、减振垫、附加质量、弹性支承、黏性护套和环境温度影响时，吊杆张力与横向振动频率解析表达式。该式为隐式，因为使用不便，但由于较全面地考虑了吊杆实际构造与边界条件的影响，因而精度较高，且适用于各长度类型吊杆。

2 构建拱桥吊杆张力实用表达式

当吊杆两端固接，则Ka,Kb→+∞和H3,H4→+∞，由式(13)可得固接边界条件下吊杆张力计算方程，即

(14)

展开可得

(15)

2.1 ξ值较大时拱桥吊杆边界影响系数

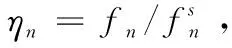
将无量纲参数ξ和ηn代入式(6)、式(7)可得

(16)

把式(16)代入式(15)，可得

(17)

由于方程中同时含有三角函数和双曲线函数，不能直接得到ηn与ξ的关系曲线。为了得到ηn与ξ关系，令

(18)

当ξ和n确定时，y(ηn)的第n零点即为ηn的值。例如，当n=2，ξ=20，y(ηn)函数图形如图3所示，从图可知：y(η2)有多个交点，取第2个零点，即η2=1.164 4。在此基础上，可获得各阶模态的ηn随ξ的变化关系。

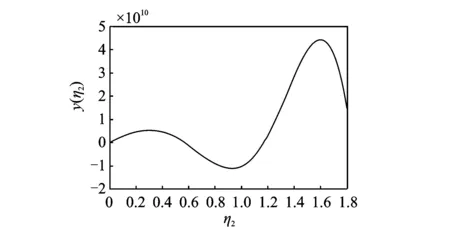
图3 函数y(ηn)与变量η2的关系曲线Fig.3 Relationship curves of function y(ηn) and versus η2

图4为吊杆前4阶模态ηn随ξ变化的关系曲线，由图可知：ηn随着ξ的增大呈现先非线性下降后逐渐趋于平缓的变化关系，最终趋近于1。当ξ较小时，ηn的变化率较高，表明吊杆振动频率对吊杆抗弯刚度较为敏感，吊杆振动类似于梁的振动。当ξ较大时，ηn的变化率较低，吊杆的振动接近于弦的振动。此时，参考简单边界条件下，吊杆的张力传统计算公式[15]为

图4 ηn与ξ的关系曲线Fig.4 Relationship curves of ηn and versus ξ

可将吊杆张力与横向振动频率关系式表示为

(21)

B1,B2为便于工程应用，在式(20)基础上引入拱桥吊杆边界影响系数，其大小与振动阶次n、吊杆两端边界条件及吊杆刚度相关。通过定义B1与B2的值，即可得到吊杆张力实用表达式，因此该方法可称为边界影响系数法。根据图4对B1,B2分段拟合定义，为了保证精度，忽略ξ较小的部分，结果如表1所示。

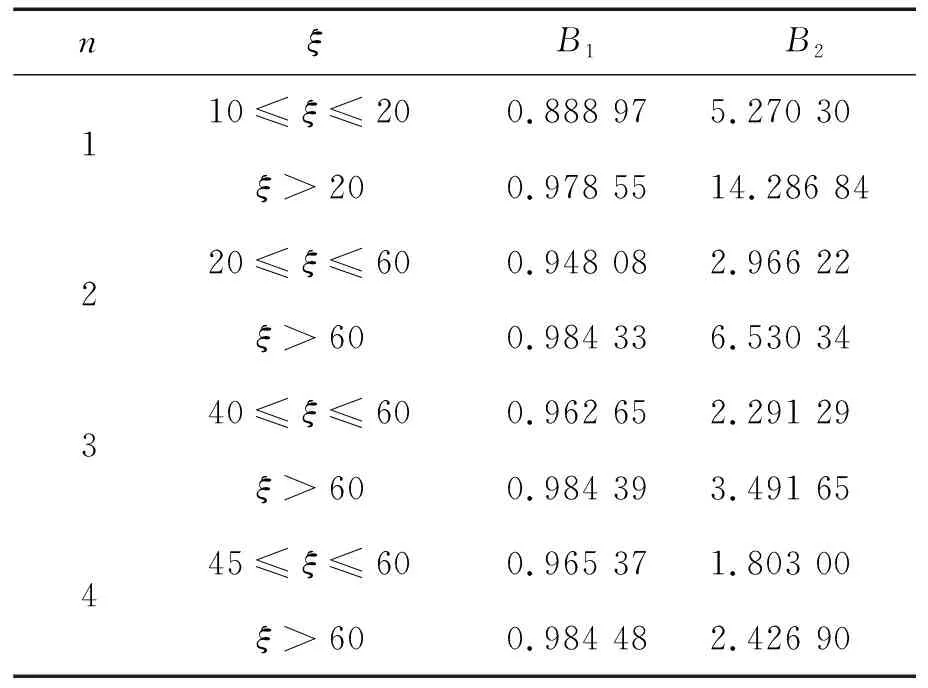
表1 ξ较大时拱桥吊杆边界影响系数表Tab.1 Influence coefficient table of arch bridge hanger boundary when ξ is larger

式(21)的精度与B1，B2密切相关，式(21)应能满足式(13),(14)。吊杆边界影响系数B1,B2与ξ,ηn关系为

(22)

当ξ较小时，吊杆做类似于梁横向振动，如按弦振动理论计算，产生的误差较大。

2.2 ξ值较小时拱桥吊杆边界影响系数

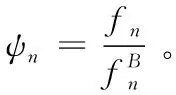
将无量纲参数ξ和ψn代入式(6)、式(7)可得

(23)

将式(23)代入式(15)可得

(24)

确定λn的值后，式(22)的求解方法同式(17)，只要给定ξ的值，即可得到ψn与ξ的关系表达式，并得到吊杆张力实用表达式。其中前4阶模态ξ与ψn的关系曲线如图5所示。

图5 ψn与ξ的关系曲线Fig.5 Relationship curves of ψn and versus ξ

由图5可知，随着ξ增大，ψn呈非线性增加，据此可定义吊杆边界影响系数B1,B2。当ξ较小时，将无量纲参数ξ和ψn代入式(21)可得

(25)

根据式(25)计算前4阶ξ不同范围时，吊杆边界影响系数B1,B2如表2所示。

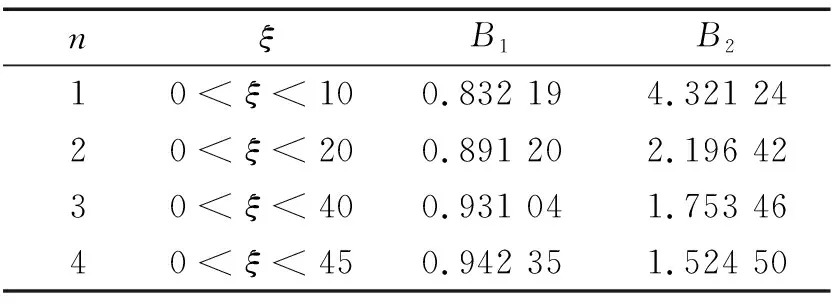
表2 ξ较小时拱桥吊杆边界影响系数表Tab.2 Influence coefficient table of arch bridge hanger boundary when ξ is smaller

2.3 拱桥吊杆张力实用表达式

考虑温度影响与吊杆黏性护套及复杂边界条件影响时，根据表1和表2拱桥吊杆边界影响系数结合式(2)与式(21)，可得前4阶模态吊杆张力与横向振动频率之间的实用表达式。

当n=1时，吊杆张力与横向振动频率之间的实用表达式为

(26)

吊杆张力与横向振动频率之间的实用表达式是分段给出的，由于各式考虑了环境温度与吊杆黏性护套及吊杆复杂边界条件的影响，因而精度较高。且公式通过吊杆边界影响系数给出，综合考虑了吊杆边界条件，从而使张力表达式更加简单，便于工程应用。

3 实例验证

以郑州刘江黄河大桥为背景，验证各式计算。由文献[15]可知，该桥采用了6种长度吊杆，该桥吊杆型号为PESC7-091，根据国家标准《斜拉桥热挤聚乙烯高强钢丝拉索技术条件》(GB/T 18365-2001)可知：钢丝束单位长度质量为27.5 kg/m；钢丝束密度为7 850 kg/m3；粘性护套采用黑色内层彩色外层双层高密度聚乙烯护套，内层护套厚为5mm，外层护套厚为3 mm，护套总厚为8 mm；吊杆外径为93 mm；吊杆单位长度质量为30.4 kg/m；抗弯刚度EI=217 120 N·m2；钢丝束公称面积为35.02 cm2；吊杆热膨胀系数为1.2×10-5/℃。

3.1 施工期吊杆张力测定计算分析

吊杆边界条件及其相关参数根据文献[15]确定。吊杆施工现场第1次张拉时横向振动频率与张力实测值如表3所示。根据表3吊杆第1次张拉实测频率值，分别采用式(19)，(20)，式(13)以及式(26)计算吊杆张力，并给出各式计算结果精度。计算结果如表4所示。

表3 刘江黄河大桥吊杆第1次张拉张力与频率Tab.3 The suspender tension and vibration frequency in the first-time tension of the Liu Jiang Yellow River Bridge

由表4可以看出，不考虑吊杆抗弯刚度时，由传统计算公式(19)计算吊杆张力，短吊杆最大误差为37.18%，长吊杆最大误差为13.56%；考虑抗弯刚度且吊杆两端铰接时，由式(20)计算吊杆张力，短吊杆最大误差为33.39%，长吊杆最大误差为12.72%；表明式(19)和式(20)相对来说更适用于长吊杆张力计算，但计算误差较大。可以看出，传统计算公式不适用吊杆张力计算。

表4 刘江黄河大桥主桥施工期吊杆张力计算值相对误差Tab.4 The calculation value and relative error of suspender tension of the Liujiang Yellow River Bridge in construction period

当考虑抗弯刚度、长度、黏性护套、减振垫、附加质量、弹性支承和环境温度等因素的影响时，由式(13)计算吊杆张力，长吊杆最大误差为1.10%，短吊杆最大误差为1.12%。结果表明，由于式(13)考虑了环境温度、黏性护套及吊杆复杂边界条件的影响，计算精度高，不仅适用于长吊杆，而且同样适用于短吊杆张力振动测试。

当根据吊杆实际情况，考虑边界影响系数，采用式(26)计算吊杆张力，各长度吊杆张力计算最大误差不超过2.38%，可以看出边界影响系数法计算精度较高，且公式形式简单、统一，实用性强。

3.2 运营期吊杆张力测定计算分析

由于表3数据为桥梁施工现场吊杆第1次张拉时实测数据，在运用式(13)与式(26)时环境温度变化为0，不能体现环境温度变化对吊杆张力的影响。为验证环境温度对吊杆张力的影响，在拱桥竣工后桥梁运营阶段实测吊杆张力如表5所示。运营测试时的环境温度为29.3 ℃；拱桥竣工完成吊杆调平张拉时环境温度为14.7 ℃。根据表5运营期吊杆振动实测频率，忽略或考虑环境温度变化时分别采用(19)、式(20)、式(13)以及式(26)计算吊杆张力，并与设计值比较计算相对误差，计算结果如表6所示。

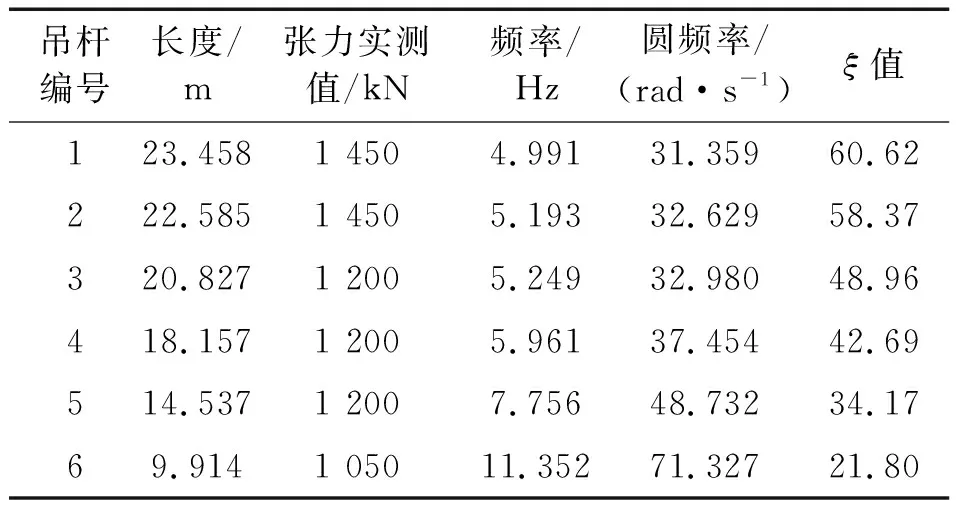
表5 刘江黄河大桥吊杆运营期实测频率Tab.5 The suspender vibration frequency of the Liujiang Yellow River Bridge in operation period

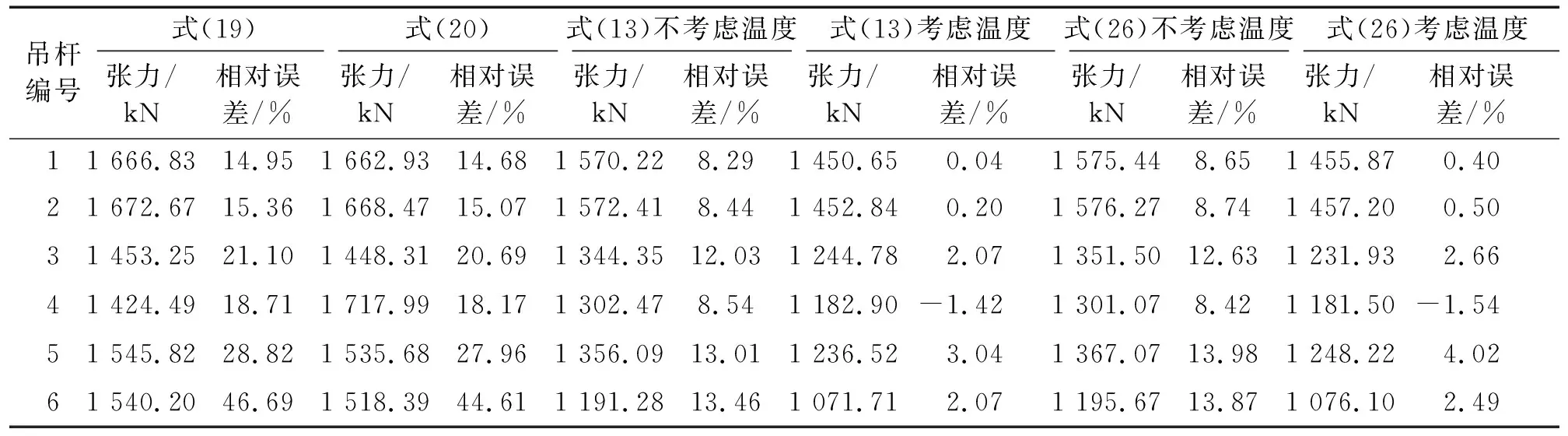
表6 刘江黄河大桥主桥运营期吊杆张力计算值相对误差Tab.6 The calculation value and relative error of suspender tension of the main bridge in operation period

由表6可以看出，对于刘江黄河大桥而言，在不考虑环境温度和复杂边界条件时，采用传统表达式计算吊杆张力时，计算值与设计值相对误差最大为46.69%，最小为14.68%。相对误差较大，主要是由于传统公式未能考虑吊杆实际边界条件与环境温度变化对吊杆张力的影响。因而不宜采用传统式(19)与式(20)计算吊杆张力，尤其是短吊杆张力计算时更需考虑吊杆实际边界条件。

采用文中提出的考虑环境温度、黏性护套与复杂边界条件影响的式(13)计算吊杆张力，不考虑环境温度变化时，计算值与吊杆张力设计值相比最大相对误差为13.46%，最小相对误差为8.29%；当考虑环境温度变化时，最大相对误差为3.04%，最小相对误差为0.04%。可以看出，两情况下式(13)计算精度均较高，考虑环境温度变化时与不考虑环境温度变化相比，精度最大提高了11.39%。

当根据边界影响系数法，采用式(26)时，不考虑温度变化影响时，吊杆张力计算值最大相对误差为13.98%，最小为8.42%；考虑温度变化影响时，吊杆张力计算值最大相对误差为4.02%，最小为0.40%。考虑温度影响时计算精度相对于不考虑温度影响时的计算精度最大提高了11.38%，可以看出在测定吊杆张力时，对于季节性温差较大的地区环境温度的影响不可忽略。

可以看出，式(13)与式(26)均体现了吊杆抗弯刚度、长度、黏性护套、减振垫、附加质量、弹性支承、环境温度等因素的影响，因而计算精度较高，均满足工程精度要求。式(26)精度略低于式(13)，主要是式(13)为综合考虑吊杆抗弯刚度、长度、黏性护套、减振垫、附加质量、弹性支承和环境温度等因素的影响时吊杆张力与横向振动频率的解析表达式，而式(26)为该式的拟合式，存在截断误差，因而计算精度略低。

此外，根据式(13)和式(26)计算运营期吊杆张力与设计值相对误差，4号吊杆误差在-1.5%左右，而相邻的3号和5号吊杆相对误差分别为2.5%和4%左右。从而可知，对于部分吊杆运营阶段张力与吊杆张力设计值比较计算误差增大，主要是由于测试时桥梁已运营多年，结构内力重分布，且部分吊杆存在局部损伤或松脱，导致该吊杆张力减小而相邻吊杆张力增大，从而导致误差增加；运营阶段由于环境温度的变化，吊杆实际张力已发生了变化，当忽略温度影响时，通过振动频率法计算得到的吊杆张力与拱桥施工竣工时吊杆张力设计值相比，必然存在一定的误差。