融合速度估计与里程计位姿的扫描匹配改进算法
2020-11-09李天剑
杨 超, 李天剑, 胡 欢, 黄 民
(北京信息科技大学机电工程学院, 北京 100192)
在移动机器人领域,机器人的位姿估计是关键性问题,关于此问题的研究进行了很多年。可以用于对机器人展开位姿估计的传感器包括激光传感器、视觉传感器、轮式编码器以及惯性测量传感器等[1]。国外以Boston Dynamics及Willow Garage为首的机器人公司主要以立体视觉为主要导航控制系统来定位与建图,而这种设备造价昂贵,至今无法实现大规模商业化[2]。小型机器人因体积小、视角低、运算能力及视场有限,即便使用廉价视觉设备,其实时理解场景的能力无法满足实际需求[3]。因此目前主流的移动机器人传感器仍以2D激光传感器为主,例如亚马逊的Kiva。同时,SLAM(simultaneous localization and mapping)技术的大规模应用使激光雷达在以扫地机器人为主的移动设备上得到了广泛应用。2D激光雷达的使用主要通过对两帧激光进行扫描匹配来估计传感器位姿[4]。扫描匹配是解决位姿估计的主要步骤[5]。迭代最邻近点(iterative closest point,ICP)算法作为解决扫描匹配问题的主流算法广泛应用于3D重建、SLAM、视觉特征匹配等领域[6]。其优势在于求解局部极值时具有较高效率[7]。
目前,2D激光匹配存在激光数据畸变以及误匹配等问题,针对误匹配问题的研究比较多,Zhang等[8]通过点到面的匹配提升室内环境下激光的匹配精度,Jo等[9]针对2D激光提出了一种错误匹配去除的鲁棒ICP算法。而对于数据畸变问题,ICP算法的匹配精度直接取决于数据是否精确,激光的捕获过程往往伴随传感器的运动,当激光帧率较小时,其捕获的激光数据与真实环境会存在误差,误差得到累积最终影响算法的最终效果,即便是建图效果较好的cartographer[10],当激光帧率较小时,其前端建图仍会面临畸变带来的建图误差,这些误差难以通过后期回环检测手段得到修复,因此针对此问题的研究具有较大的实际意义。Bezet等[11]曾对激光雷达的扫描畸变问题展开过具体研究,他们根据时间误差对此问题进行修正。但该方案的角度固定与二次插值假设过于简单化,无法满足更为一般的室内环境。Hong等[12]针对此问题提出VICP(velocity updating iterative closest point)算法,该算法是ICP算法的另一变种,算法考虑机器人的运动,认为激光雷达在扫描过程中进行匀速运动,并进行速度估计。该算法有效解决了激光运动过程中机器人的位姿估计问题,但其关于匀速运动的假设过于理想,以5 Hz激光雷达为例,激光捕获一帧数据所需时间为200 ms,这对于以1~2 m/s运动的室内机器人而言是不可忽略的时间间隔,匀速运动的假设并不适用。Zhang等[13]曾在3D激光算法的扫描匹配算法中采用速度估计算法对运动畸变进行去除,并应用于SLAM技术,但匀速假设的缺陷仍然存在。
针对以上问题,提出一种创新算法,融合速度估计与轮式里程计位姿估计对ICP算法进行改进。
1 基本算法
ICP算法的初始阶段依赖初始位姿估计与两帧激光数据展开坐标变换,通过重复捕捉最邻近点来迭代优化激光匹配,获取坐标变换,并将最终累计误差最小化。ICP算法在栅格尺度上会单调收敛于局部极值,因此对初始位姿有较高要求,若初始位姿离真值偏差较大,ICP算法将最终收敛于局部最小值,非全局最小值,因此在初始阶段对初始位姿进行优化,此时可通过里程计进行初始估计[14]。
假设X={xi}为一帧激光数据,Y={yi}为下一帧激光数据。主要目标在于寻求X与Y之间的坐标变换以使X与Y实现最大化匹配。最小化目标函数定义如下:
(1)
式(1)中:R为旋转矩阵;p为平移矩阵。
该目标函数的处理步骤如下:
(1)给定xi代表X中的激光点位置,yi代表Y中与xi对应的激光点位置。
(3)对点云进行平移操作,将点云平移到以平均值为圆心的位姿处X′={xi-ux}={x′i},Y′={yi-uy}={y′i}。
(4)构造W矩阵并进行奇异值分解(SVD):
(2)
(5)求解得到关于目标函数的解:R=UVT,p=ux-Ruy。
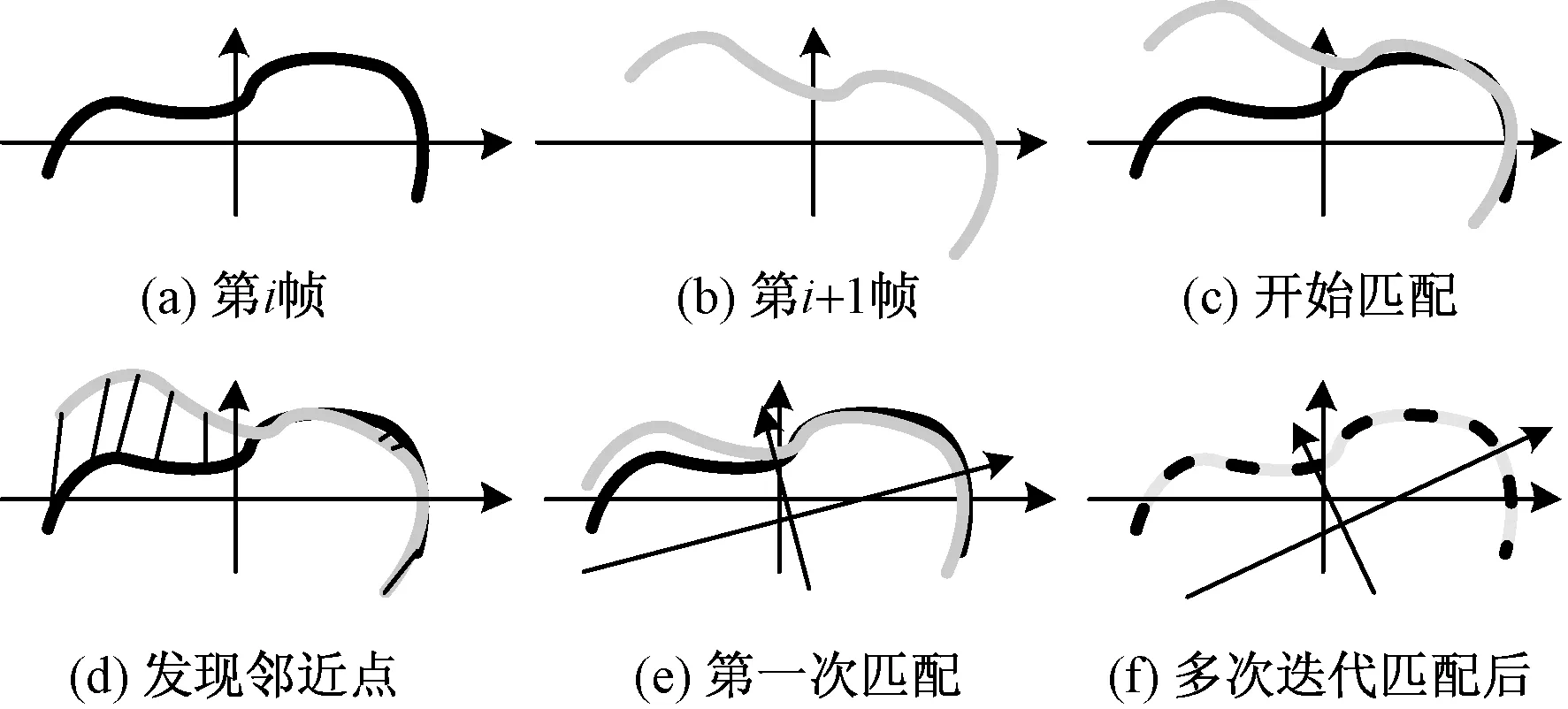
图1 ICP算法流程Fig.1 ICP diagram flow
由于ICP算法使用最邻近点作为对应点,对初始值就会相对敏感。当初始值与真实环境不完全接近时,重复迭代过程会让最终的结果尽可能收敛于真实状态[15]。图1展示了ICP算法流程,图1(a)、图1(b)为第i帧第i+1帧扫描,图1(c)为匹配开始,从图1(d)中展开的迭代过程发现了X与Y帧中的邻近点,第一次迭代后,ICP得到了X与Y之间的估计坐标变换T1,通过坐标变换可对Y进行位姿调整,如图1(e)所示。通过重复迭代过程,最终可使Y与X达到接近状态,如图1(f),最终的坐标变换通过T=Tn,Tn-1,…,T1来求解最终的位姿估计。
xi=TnTn-1…T2T1yi,i=1,2,…,n
(3)
算法流程如下:
输入:激光点集Xi,Yi
输出:最终位姿变换T
T=T0
While ||T′|| >e do
For k=1:n do
yk=Tyk//对激光点进行位姿变换
End for
For k=1:n do
xk=FindClosetPoint(X,yk)//迭代寻找邻近点
End for

For k=1:n do
x′k=xk-xm;y′k=yk-ym//将xk,yk做平移
End for
[U,S,V]=SVD(∑y′k⊗x′k)//进行SVD分解
R=UVT//得到旋转向量R
p=xm-Rym//得到平移向量p
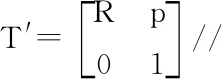
T=T′T//将变换矩阵迭代相乘
End while
Return T
2 激光雷达环境扫描畸变问题分析
每帧激光数据都由数量固定的离散激光束组成[16]。一帧激光数据的捕获并非瞬时发生。激光雷达的扫描畸变与激光雷达捕获数据时机器人的运动转换有关。假设以搭载2D激光雷达的移动机器人为研究对象,机器人通过激光雷达获取环境数据,当激光雷达对环境进行一帧数据扫描时,机器人很可能在此时间段内存在运动变换,这就造成了对环境的错误表达。也就是说,其数据捕获过程不可避免的会伴随机器人的运动,当激光雷达帧率较低时,机器人的运动就不能被忽略,尤其在机器人进行旋转运动时,激光雷达的数据畸变会尤其明显。
以图2所示环境为例,A为机器人捕获第i帧数据的初始位姿,当机器人完成第i帧数据的捕获,进行i+1帧数据扫描时,机器人移动到B点所示位置,那么,从A点到B点的过程机器人恰好完成了一帧数据的捕获,在这个过程中,激光雷达会向图示环境发射离散的激光束,假设机器人在A点发射了第i束激光束,而在途中的C点发射了第i帧激光中的第j束激光束。
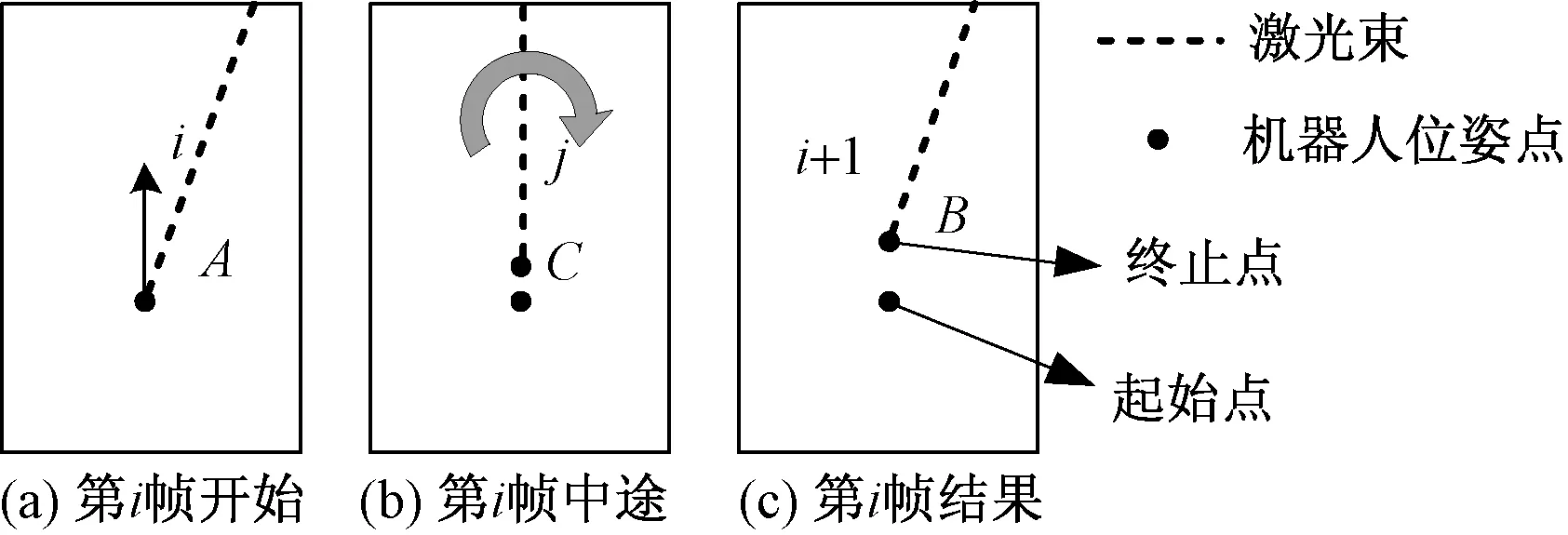
图2 第i帧激光Fig.2 ith frame laser
当机器人捕获一帧数据时,机器人会将这一帧数据打包进行处理,也就是说,机器人捕获一帧数据的过程中,会认为其自身位姿未发生变化,但正如上面的情况所述,机器人在捕获一帧环境数据时,它的自身位姿实际上产生了运动变化。机器人完成一帧数据捕获后对第i帧数据进行打包处理时,认为第j束激光束发生时其位姿仍为A点,最终造成环境畸变,如图3所示。
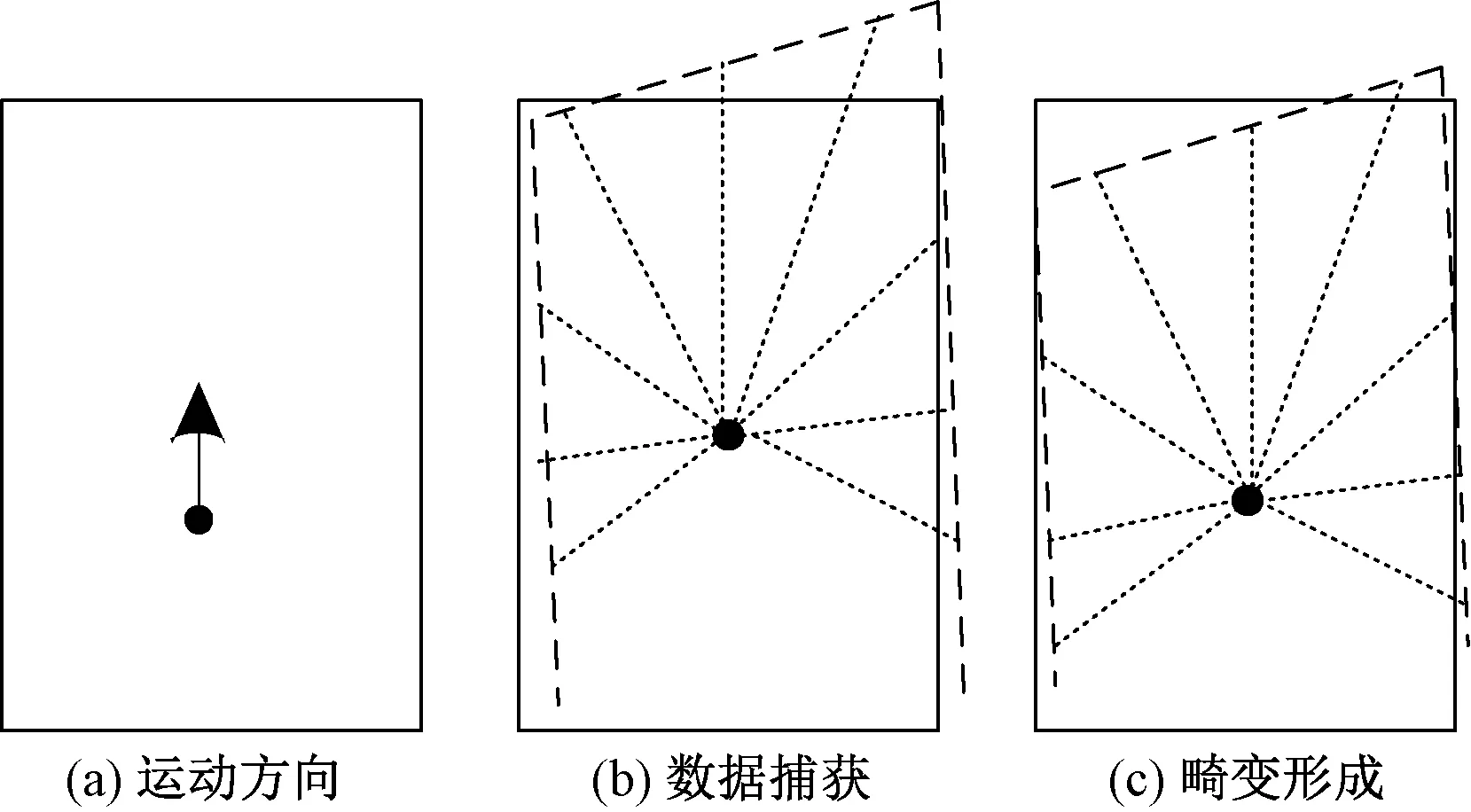
图3 激光扫描失真问题形成Fig.3 Results of the laser scanning distortion problem
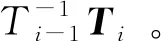
(4)
3 里程计位姿与速度估计融合
3.1 引入里程计位姿估计
为补偿激光扫描数据,引入里程计信息对激光雷达位姿展开估计,具体是对一帧激光中的每束激光对应的机器人位姿通过里程计信息进行补偿。而为实现通过里程计信息对激光雷达位姿进行估计,需要求里程计的更新频率远高于激光雷达,同时里程计需能够对机器人的旋转和平移运动进行同时测量和估计,因此选用轮式编码器作为里程计。
假设存在激光帧位姿队列与里程计位姿队列分别为Ps0,Ps1,…,Psm;Oo0,Oo1,…,Oon。其中,Psi代表第i束激光束对应的机器人位姿,Ooi代表里程计测量得到的机器人在oi时刻位姿。事实上,在一般情况下,里程计位姿队列并不能与激光帧位姿队列保持严格对齐。此时由于二者位姿队列非严格对齐,无法直接从里程计位姿队列中获取激光帧位姿,此时可通过对里程计线性插值获取激光帧位姿。
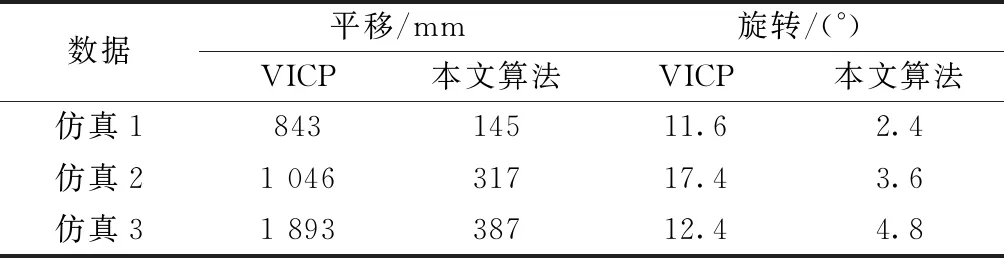
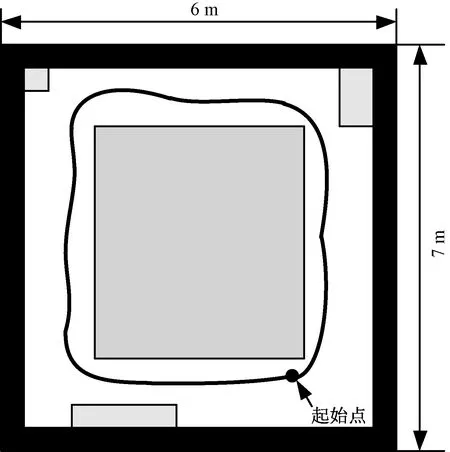
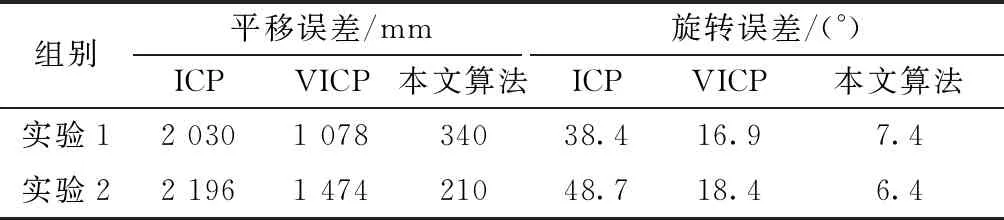
首先求取激光帧起始位姿,以激光帧开始位姿Ps0为例,假设里程计位姿队列中存在位姿OL、OK,且TL Ps0=(OKOL)αOL,α∈[0,1] (5) 式(5)中:Ps0、OK、OL∈ SO(3),且α=(Ts0-TL)/(TK-TL)。 同理可求得激光帧终止位姿Psm。 此时,从激光帧位姿队列中取K个位姿(K>3),对激光帧位姿队列进行分段: Ps0,…,Psk1,Psk2,…,Psm [Ps0,…,Psk1] [Psk1,…,Psk2] ⋮ [Psk,Psm]。 其中,K个位姿中每个位姿都通过对里程计位姿队列进行线性插值获取。随后需要通过分段点位姿对每个队列子集中的激光点位姿进行位姿转换: x′i=PTxi (6) 式(6)中,x′i为转换后激光点位姿;xi为转换前激光点位姿;P为分断点机器人位姿(里程计位姿)。 算法2实现如下: 输入:里程计位姿队列P 激光位姿队列X 输出:激光队列Xn Ps=LinarInterp(Odemtery);Pe=LinarInterp(Odometry)//对起始位姿进行里程计线性插值 For beamnumber=1:n do//按每帧激光点数进行循环 If t>interpolation_time_duration then//设定相应的分段时间 Pmid=LinarInterp(Odometry)//对分段点进行里程计线性插值 While i End While P=Pmid//更新分断点 End if end 对机器人位姿进行分段处理后,需对分段子集激光点进行再次数据补偿。此时对子集内激光雷达的速度进行估计。假设在扫描时间范围内雷达的速度是恒定的。以Vi表示雷达在ti时刻的速度。首先,从两帧相邻激光数据集中对应子集Xi和Xi-1之间的相对运动变换中估计速度Vi为 (7) 估算速度Vi用于进一步转换子集Xi中的每个激光坐标点。假设Xi中的激光点数量为n,相邻激光点之间的时间间隔为Δt,那么,x0,x1,…,xn为Xi中的激光点,同时txj-txj-1=Δts(j=0,1,…,n-1)。在Xi中的每个激光点有自己的局部坐标系,短时间内的运动变换T(ti+jΔts)如下: T(ti+jΔts)=TiejΔtsVi (8) (9) 通过式(8)与式(9)可将点集进行运动转换。当点集中第一个激光点被捕获时,式(9)所述点集的运动转换就会发生。由于第一个激光点与最后一个激光点之间存在不小的时间间隔,这会造成与实际运动之间的延时。为处理这一问题,采用后向补偿,以最后一个激光点对应时间为参考时间ti,每个激光点对应时刻为[ti-nΔts,ti-(n-1)Δts,…,ti-Δts,ti]。因此,式(7)修改为 T[ti-(n-j)Δts]=Tie(n-j)Δts(-Vi) (10) 式(9)也被修改为 (11) 算法的具体实现如下: 输入:激光点集X 输出:运动变换T Vi=Vi-1//速度初始化 TΔts=eΔts(-Vi)//通过速度估计运动变换T For j=n:1 do//对每个激光点执行以下循环 TjΔts=T(j-1)ΔtsTΔts//计算每个激光点运动变换 End for V=Vi//速度更新 Vi=1/ΔlgT//进行下一次速度估计 End while 通过仿真环境分别对VICP与本文改进ICP算法进行仿真对比实验。仿真环境使用turtlebot3[17]机器人搭载激光雷达为激光设备,其激光扫描半径为3.5 m,5 Hz扫描频率(每帧200 ms),360°扫描范围,每帧激光包含360个激光点(1°角分辨率)。测试设备处理器为INTEL CORE I7-6560U CPU 2.20 GHz,内存8 GB。 设置三种仿真环境,在仿真环境中,机器人以1 m/s速度运动,通过里程计及激光雷达,同时以里程计、VICP及本文算法记录三条机器人运动轨迹。由于仿真环境中的机器人里程计不存在打滑与安装误差的问题,这里将里程计得到的轨迹作为真值,同时分别通过VICP及本文算法分别在三种仿真环境中对两种算法进行测试。得到仿真结果如图4所示。 图4 仿真实验及轨迹Fig.4 Simulation experiment and trajectory 图5 VICP及本文算法误差对比Fig.5 The error comparison of the VICP and our algorithm 根据里程计,本文给定了机器人的真实运动轨迹,以此轨迹为真值对三种算法误差进行分析,分别取关键帧里程计位姿间平移与旋转变换与VICP以及本文算法对应激光帧间平移与旋转变换进行对比,误差如图5所示,可看出,本文算法的帧间匹配效果更接近于真值(里程计),误差小于VICP。同时分别记录平移与旋转的累计误差,量化两种算法的误差对比,累计误差对比如表1所示。 从仿真实验效果来看,在三种不同环境中,VICP与真值轨迹偏离较远,帧间平移与旋转偏差较真值相差较大,而本文算法轨迹与真值轨迹较为贴合,帧间平移与旋转偏差较真值相差脚下。而表1累计误差显示,VICP与本文所示算法相比,本文算法结果更优,在三种仿真环境中的激光匹配效果,本文所述算法匹配效果更好,无论平移与旋转误差,都明显低于VICP。 表1 仿真累积误差Table 1 Accumulated error of simulation experiment 真实实验环境为42 m2大小的厅(图6)。使用turtlebot3_waffle_pi为实验平台,激光雷达参数与仿真环境相同图7。所有算法的实现采用C++语言,实现平台为笔记本计算机,搭载INTEL CORE I7-6560U CPU 2.20 GHz,内存8 GB。由于真实环境中,机器人的真值轨迹无法精确获得,因此采用回环的方式将起始位姿与终止位姿重合,通过算法对机器人位姿进行还原,以回环效果判断算法的误差累计,实验平台由人员远程操控。 图6 环境示意图Fig.6 Environmental diagram 图7 实验平台及环境Fig.7 Experimental platform and environment 图6展示了实验环境平面图与移动机器人回环大致轨迹,机器人从起点到终点完成一个回环,实验中机器人分别以平均0.5 m/s及1 m/s速度运动,激光雷达收集到相应激光数据集,将此数据集用来进行对比实验。分别通过轨迹展示了三种算法在同一数据集下的位姿还原效果,如图8、图9所示。 图8 ICP与本文算法轨迹对比Fig.8 The trajectory comparison of ICP and our algorithm 图9 VICP与本文算法轨迹对比Fig.9 The trajectory comparison of VICP and our algorithm 图8、图9所示轨迹显示,在不同运行速度下,图8中,原始ICP算法在激光雷达的连续畸变效果下,其误差累积导致无法完成回环,与真实运动轨迹存在较大误差,本文改进ICP算法基本完成了回环,其误差累计远小于原始ICP算法。图9为VICP与本文算法对比,VICP算法的回环效果好于原始ICP,但仍然出现了轨迹交叉等误差,并未真正回环,其轨迹也存在不同程度与真实轨迹的偏移,本文改进ICP算法相较VICP更为接近真实轨迹状态,最终的回环累计误差如表2所示。 表2 实验累计误差Table 2 Accumulated error of experiment (1)激光帧率较低时,雷达的运动会带来不可忽略的扫描畸变问题,影响最终的ICP算法匹配效果。 (2)单纯的速度估计及匀速假设并不能有效消除扫描畸变对ICP匹配的影响,尤其在雷达运动速度并非缓慢的情况。 (3)将里程计辅助位姿估计及速度估计相融合,能够提供较为精确的激光点位姿,仿真实验及真实场景实验均表明,与原始ICP算法及融合速度估计的VICP算法相比,本文算法能够更好地还原真实的位姿轨迹。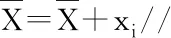
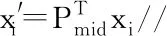
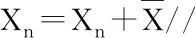
3.2 速度估计与数据补偿
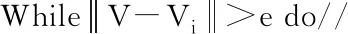
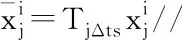
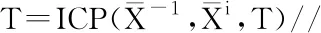
4 仿真实验


5 实验与分析



6 结论
