含饱和特性的双采样率数据Hammerstein系统辨识
2020-11-09王宏伟陈瑜潇
王宏伟, 陈瑜潇
(1.新疆大学电气工程学院, 乌鲁木齐 830047; 2.大连理工大学控制科学与工程学院, 大连 116024)
在工业实际生产过程中,受传感器采样频率、物理设备、人工采样、机械振动、网络传输等因素的影响,使得系统采样呈现输入信号的刷新时间和输出信号的采样时间是不相同的, 此类系统是多采样率数据系统。对于多采样率线性数据的线性系统,利用变量提升技术[1-5]、多项式转换技术[6-10]。结合多信息最小二乘类辨识算法,在不同模型结构下,如ARMAX(auto-regressive moving average exogenous)、Box-Jenkins、输出误差类模型等,研究者们创新性地提出了很多辨识算法,取得了很好的辨识建模效果。但是,实际工业系统往往呈现非线性,很难使用线性系统的辨识方法来辨识多采样率的非线性系统。本文以双采样率数据的非线性系统为辨识对象开展研究,图1给出此类系统的结构图。
对于双率采样的Hammerstein非线性系统,文献[11]提出了变量提升技术和最小二乘算法辨识方法,但是利用变量提升技术后的系统往往向量维数较大,对算法的收敛性没有分析;文献[12]针对含有有色噪声的多采样率数据非线性系统,提出基于递阶原理的随机梯度辨识算法解决含有有色噪声的多采样率非线性系统辨识问题,算法收敛性也进行了探讨;文献[13]采用多新息随机梯度辨识方法分别对非均匀采样数据Hammerstein-Wiener系统和Wiener系统进行了建模研究;针对采用提升技术往往使系统变量、参数个数增加,模型结构复杂的问题,文献[14]基于递阶原理将含有提升变量的系统模型辨识转化为若干个子系统的辨识,这样算法简单、计算量小,效率高;针对含饱和死区特性的Hammerstein系统,文献[15]提出了借助递推思想和辅助模型思想估计内部未知变量,在此基础上利用梯度辨识法进行参数进行估计。文献[16-17]通过模糊建模方法解决了非均匀采样的复杂非线性系统辨识问题。采用模糊聚类解决模糊模型前提结构和参数问题,利用递阶最小二乘算法解决模糊模型后件参数估计,同时对算法收敛性进行了研究。文献[18]通过新型粒子滤波器而非辅助模型来估计不可测输出量,利用梯度迭代算法进行系统辨识,仿真效果表明该方法与经典辅助模型算法相比更有效。文献[19]将噪声分布利用t分布表示,将未知时间延迟作为潜在变量,利用条件期望最大化对时间延迟未知且具有异常值的双率输入非线性方程误差系统进行了参数辨识,仿真效果表明该方法辨识结果更精确。文献[20]令同一被估计参数利用前三次估计值迭代得到新估计值,与传统基于辅助模型的随机梯度算法相比提高了收敛速率,且采用改进的卡尔曼滤波方法提高了辨识精度。
针对双率采样的Hammerstein非线性系统的辨识,一般都是针对模块化的Hammerstein模型、Wiener模型、Hammerstein-Wiener模型、Wiener-Hammerstein模型展开的,其非线性模型一般是由静态非线性环节和线性动态环节串联组成的,其中非线性环节一般是由非线性多项式组成的,但实际工业系统中也有其他静态非线性特性,例如滞后特性,死区特性、间隙特性、继电器特性、饱和特性等,其中饱和特性是实际控制中经常遇到的,例如化工过程的电磁阀门输入输出特性、控制器放大器的饱和特性等。这些非线性系统的辨识遇到的困难主要为:①被辨识参数间存在交叉耦合和交叉乘积项;②含有很多未知的中间变量;③含有采集不到的缺失数据。本文针对含有饱和特性的非线性系统的辨识问题,基于双采样率数据开展了辨识建模的研究。
1 含有饱和特性的双采样率的Hammerstein系统模型
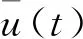

图1 双采样率数据的Hammerstein系统结构Fig.1 Structure of Hammerstein system with dual-rate sampling data
对于图1的Hammerstein非线性系统,其中线性动态环节为
y(t)=x(t)+v(t)
(1)
(2)
式(1)中:A(z)和B(z)是单位后移算子z-1[z-1y(t)=y(t-1)]的多项式,它们分别为A(z)=1+a1z-1+a2z-2+…+anaz-na、B(z)=b1z-1+b2z-2+…+bnbz-nb,其中ai和bi是多项式中的参数。本文中取b1=1。
图1中,静态非线性环节f(·)是饱和特性非线性函数,其输入输出关系如图2所示。
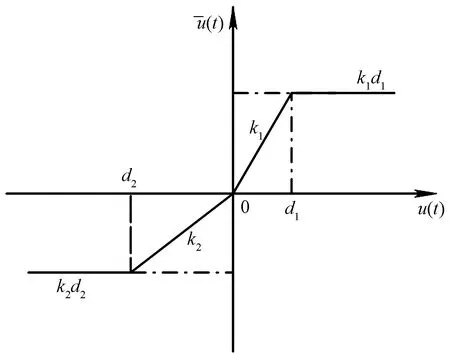
图2 饱和特性非线性函数Fig.2 Function of saturation nonlinearity
饱和特性非线性函数可以表示为
(3)
式(3)中:k1、k2分别为正、负线性部分的斜率;k1d1、k2d2分别为正、负线性部分的上、下限值。式(3)是分段线性函数,为了计算方便,可以将式(3)写为
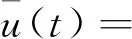
k1u(t)h[u(t)-d1]-k1d1h[u(t)]h×
[d1-u(t)]+k2u(t)h[-u(t)]+
k2d2h[-u(t)]-k2u(t)h[d2-u(t)]-
k2d2h[-u(t)]h[u(t)-d2]
(4)
式(4)中:h(t)是开关函数,即
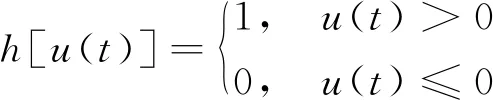
(5)
对于式(5),可以转变为一些非线性基函数fj[u(t)]的展开,即
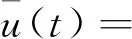
c4f4[u(t)]+c5f5[u(t)]+c6f6[u(t)]+
(6)
式(6)中:c1=k1;c2=k1d1;c3=k1;c4=k2;c5=k2d2;c6=k2;c7=k2;c8=k2d2;基函数为f1[u(t)]=u(t)h[u(t)],f2[u(t)]=h[u(t)],f3[u(t)]=-u(t)h[u(t)-d1],f4[u(t)]=-h[u(t)]h[d1-u(t)],f5[u(t)]=u(t)h[-u(t)],f6[u(t)]=h[-u(t)],f7[u(t)]=-u(t)h[d2-u(t)],f8[u(t)]=-h[-u(t)]h[u(t)-d2]。
当然,式(6)又可以写成向量表达式:
(7)
式(7)中:f[u(t)]={f1[u(t)],f2[u(t)],f3[u(t)],f4[u(t)],f5[u(t)],f6[u(t)],f7[u(t)],f8[u(t)]}T∈R8,c=[c1,c2,c3,c4,c5,c6,c7,c8]T∈R8。
定义输入信息向量φ(t)和参数向量θ分别为
φ(t)={-x(t-1),-x(t-2),…,-x(t-na)
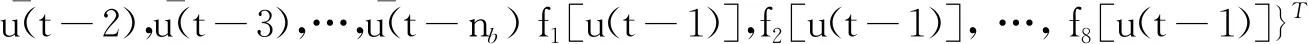
这样根据式(1)、式(2)就有:
y(t)=φT(t)θ+v(t)
(8)
辨识的目的:利用双率采样数据{u(k),y(kq)},k=1,2,3,…,对静态非线性模块f(·)和动态线性模块G(z)中的参数进行辨识。为此,用kq代替t就有:
y(kq)=φT(kq)θ+v(kq)
(9)
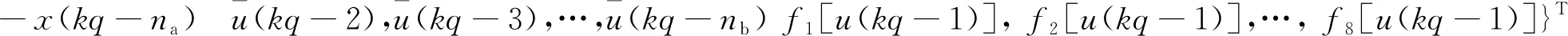
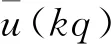
(2)非线性基函数fj[u(kq+i)],j=1,2,…,8,i=0,1,…,q-1也是未知的。为此,借助于辅助模型的输出作为非线性基函数的估计。
2 基于辅助模型原理的递推辨识
为了实现参数辨识,定义准则函数为
(10)
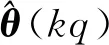
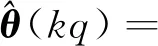
(11)
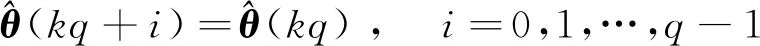
(12)
(13)
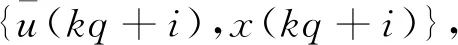
定义变量:
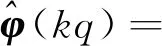
(14)
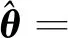
(15)
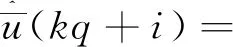
i=0,1,…,q-1
(16)
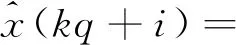
i=0,1,…,q-1
(17)
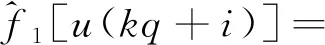
i=0,1,…,q-1
(18)
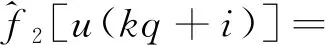
i=0,1,…,q-1
(19)
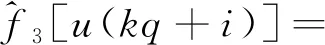
(20)
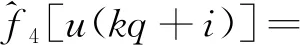
u(kq+i)],i=0,1,…,q-1
(21)
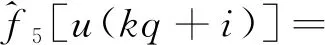
i=0,1,…,q-1
(22)
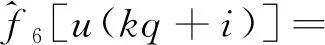
i=0,1,…,q-1
(23)
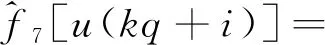
(24)
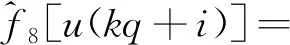
(25)
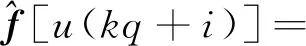
i=0,1,…,q-1
(26)
定义多个辅助模型后,基于辅助模型的递推最小二乘辨识算法如下:
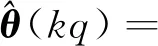
(27)
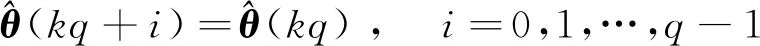
P(kq)=P(kq-q)-
(28)
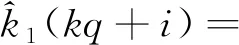
i=0,1,…,q-1
(29)
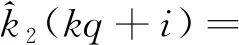
i=0,1,…,q-1
(30)
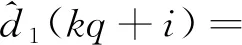
i=0,1,…,q-1
(31)
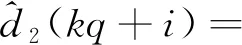
i=0,1,…,q-1
(32)
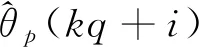
下面将整个辨识算法完整总结如下:
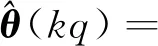
(33)
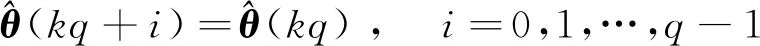
(34)
P(kq)=P(kq-q)-
(35)
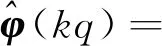
(36)
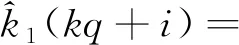
i=0,1,…,q-1
(37)
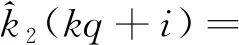
i=0,1,…,q-1
(38)
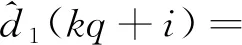
i=0,1,…,q-1
(39)
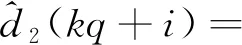
i=0,1,…,q-1
(40)
(41)
(42)
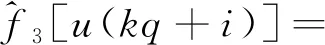
(43)
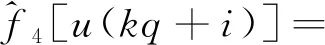
u(kq+i)]
(44)
(45)
(46)
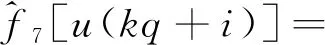
u(kq+i)]
(47)
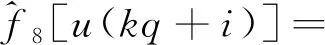
(48)
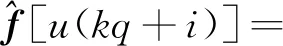
(49)
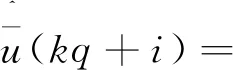
i=0,1,…,q-1
(50)
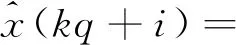
i=0,1,…,q-1
(51)
下面将基于双率采样数据的Hammerstein系统辨识过程总结如下:
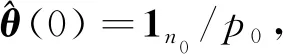
(3)根据式(35)计算P(kq)。
(6)令k=k+1, 如果k≤N转到步骤(2)。
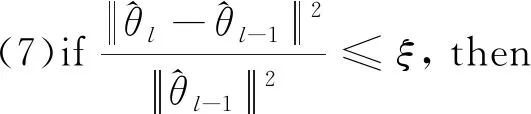
图3给出上述参数辨识算法的流程框图。
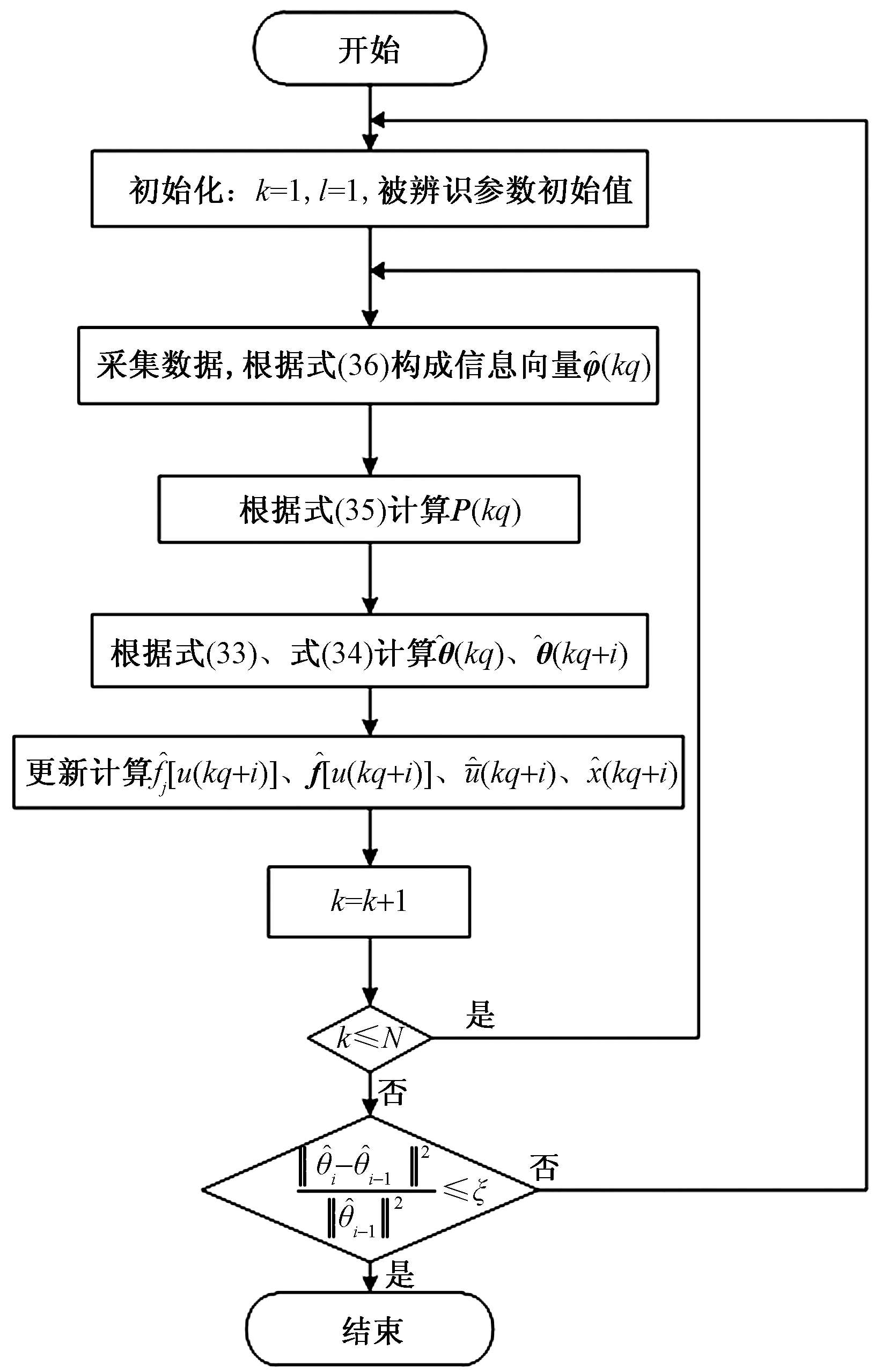
图3 参数辨识算法的流程框图Fig.3 Flow chart of parameter identification algorithm
3 仿真算例
考虑下列含饱和特性的Hammerstein系统:
(52)
饱和特性非线性函数为
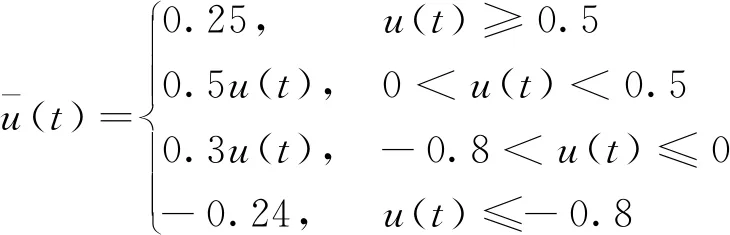
(53)
式中:A(z)=1+0.4z-1+0.3z-2,B(z)=1+0.5z-1+0.6z-2;v(k)分别是零均值,方差为σ2=0.0152、0.0252、0.0452的白噪声;饱和特性非线性函数的参数为:k1=0.5,k2=0.3,d1=0.5,d2=-0.8。取双率系数q=2,p0=1×106。
对于仿真实例的辨识模型,需要辨识的参数向量θ=[a1a2b1b2c1c2c3c4c5c6c7c8]T=[0.4 0.3 0.5 0.6 0.5 0.25 0.5 0.25 0.3 -0.24 0.3 -0.24]T。
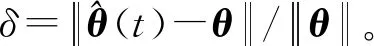
图4~图11、表1~表6给出了辨识的结果,可以得到如下结论。
(1)在不同噪信比下参数估计误差都随着t的增加而减小,而且估计误差减小速率很快,辨识精度较高。
(2)在不同噪信比下,参数估计相对误差分别为1.148 5%、1.244 2%、3.083 1%,误差变化不大,说明在不同噪信比下,在双率采样数据下,提出的辨识算法都能够满足参数估计的要求。
(3)在不同噪信比下,噪信比越大,参数估计精度越低,且估计值逼近真值的速率越低。
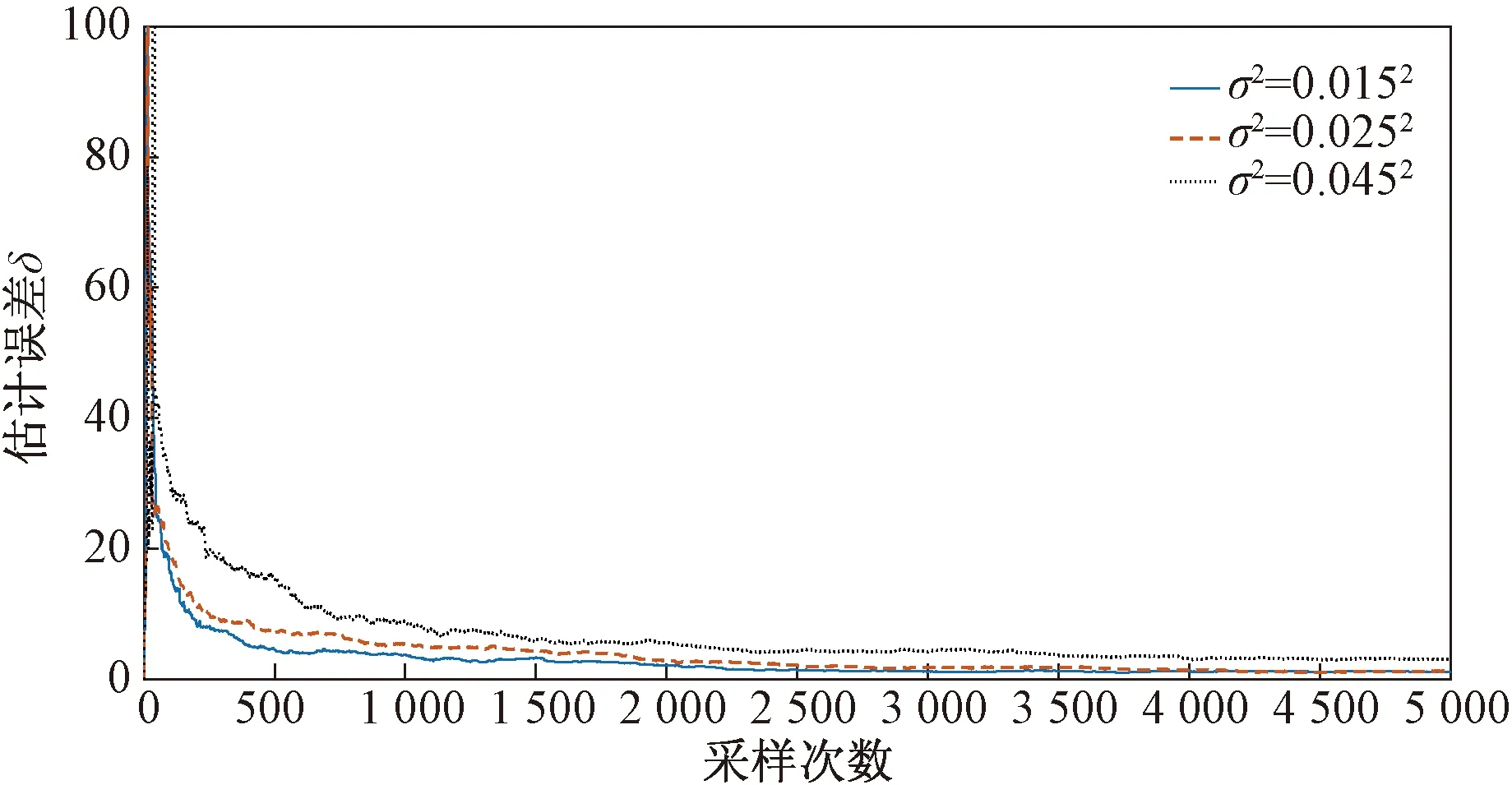
图4 相对参数估计误差曲线Fig.4 Relative parameter estimation error curve
4 结论
基于辅助模型思想, 提出辅助模型的最小二乘算法辨识双采样率的含饱和特性的Hammerstein非线性系统,仿真结果验证了该算法的有效性。Hammerstein非线性系统虽然已经有了大量的研究基础,但是其在双率采样条件下还有非常广泛的、深入的研究空间,例如滞后非线性特性,死区非线性特性,继电器非线性特性等,特别是继电器非线性特性的研究较少,因此这方面后续的研究是非常有意义。
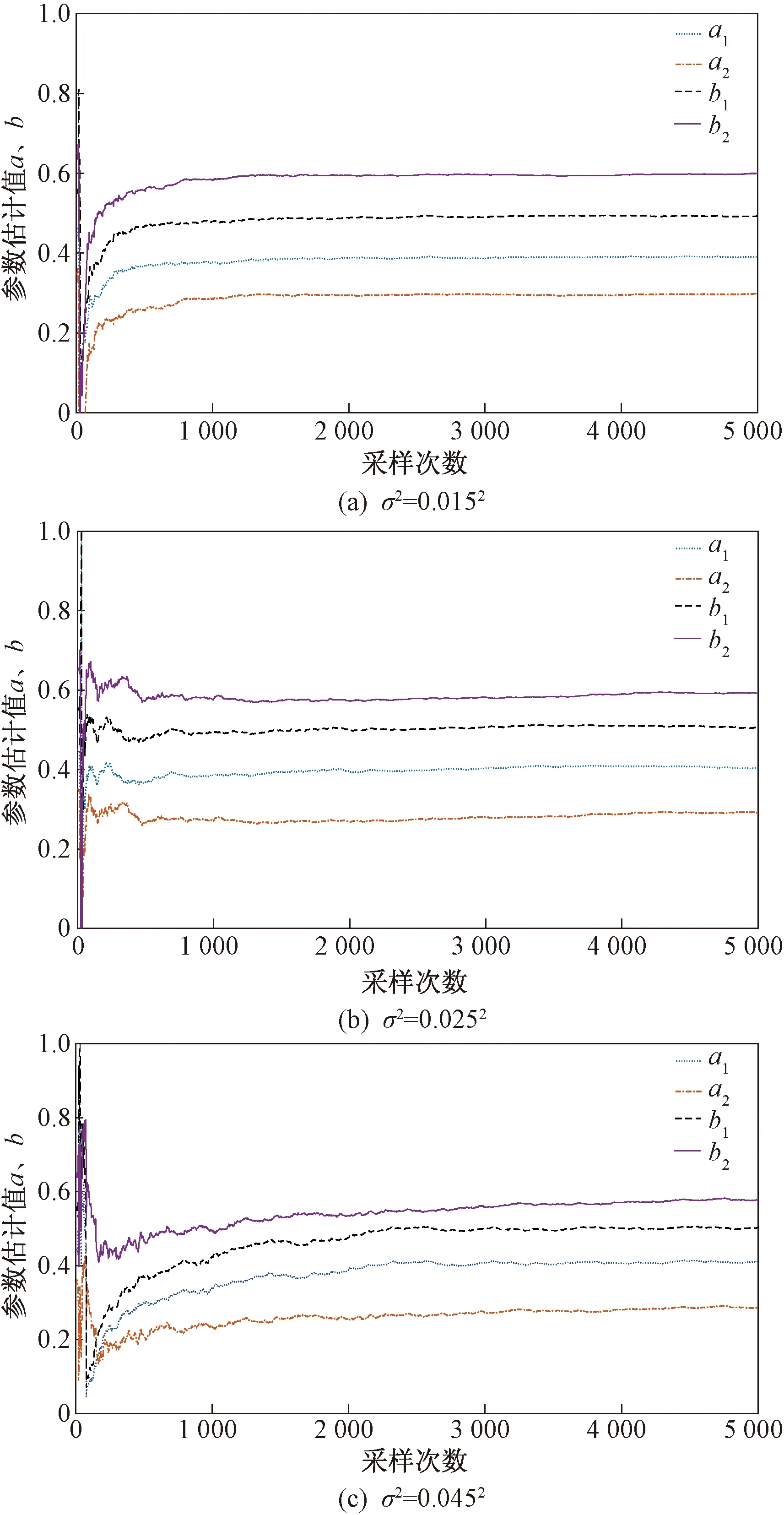
图5 参数a、b估计值曲线Fig.5 Parameter estimation curve of a,b
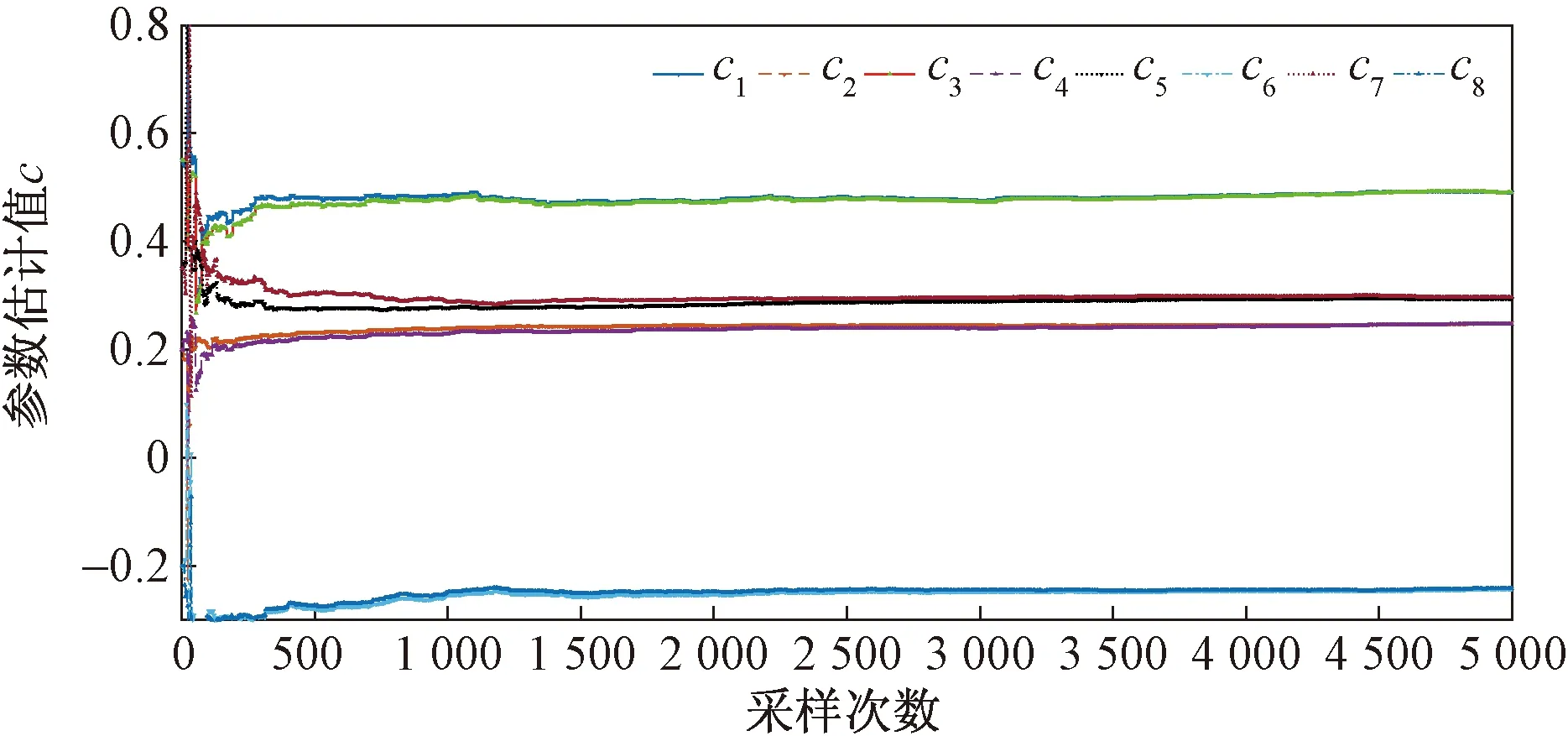
图6 σ2=0.0152时参数c估计值曲线Fig.6 Parameter estimation curve of c while σ2=0.0152
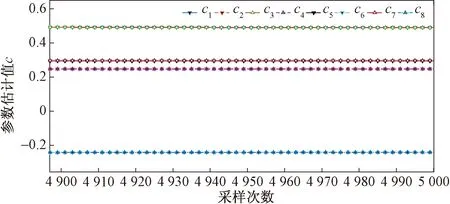
图7 图6局部放大图 Fig.7 Detailed view from fig.6
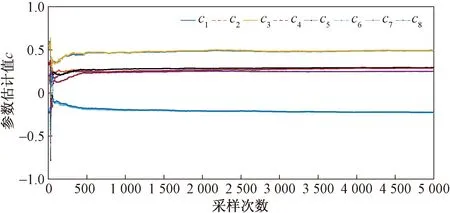
图8 σ2=0.0252时参数c估计值曲线Fig.8 Parameter estimation curve of c while σ2=0.0252
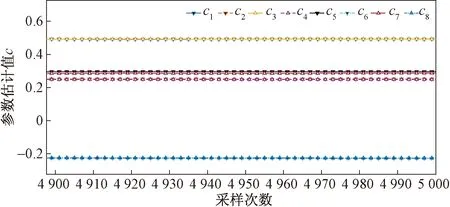
图9 图8局部放大Fig.9 Detailed view from fig.8
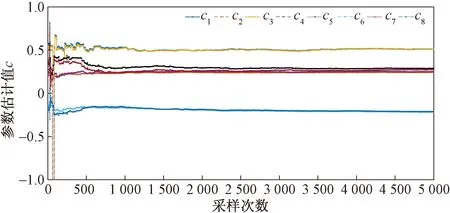
图10 σ2=0.0452时参数c估计值曲线Fig.10 Parameter estimation curve of c while σ2=0.0452
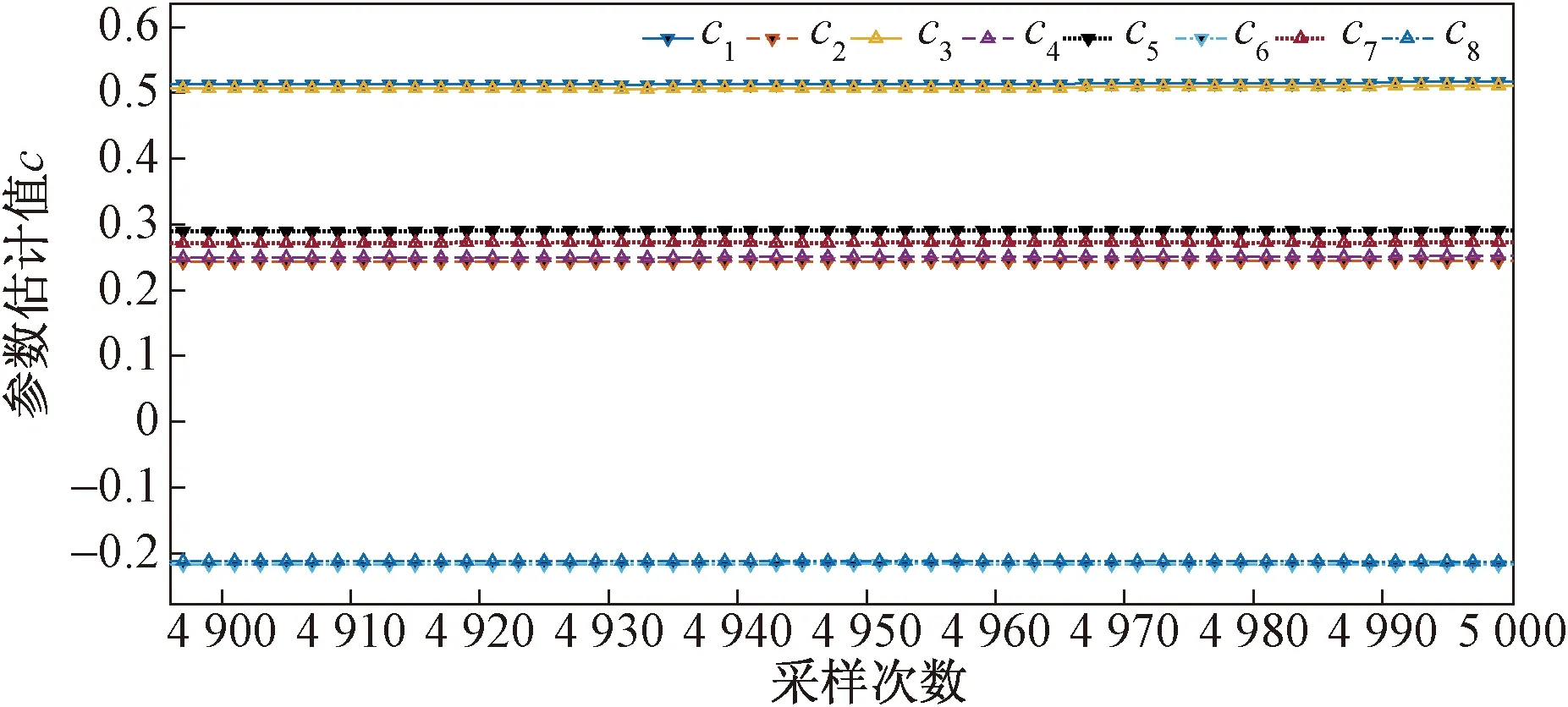
图11 图10局部放大Fig.11 Detailed view from fig.10

表1 辨识得到的参数a、b及相对估计误差(σ2=0.0152,δns=6.705 9%)Table 1 Parameter estimation of a,b and relative estimation error(σ2=0.0152,δns=6.705 9%)

表2 辨识得到的参数c(σ2=0.0152,δns=6.705 9%)Table 2 Parameter estimation of c (σ2=0.0152,δns=6.705 9%)

表3 辨识得到的参数a、b相对及估计误差(σ2=0.0252,δns=11.216 6%)Table 3 Parameter estimation of a,band relative estimation error(σ2=0.0252,δns=11.216 6%)

表4 辨识得到的参数c(σ2=0.0252,δns=11.216 6%)Table 4 Parameter estimation of c (σ2=0.0252,δns=11.216 6%)

表6 辨识得到的参数c(σ2=0.0452,δns=20.117 7%)Table 6 Parameter estimation of c (σ2=0.0452,δns=20.117 7%)
