马赫数对压气机失稳静压升系数影响的数值模拟

2020-09-16魏婷，胡骏

航空发动机 2020年4期

魏婷，胡骏

（南京航空航天大学能源与动力学院，南京210016）

0 引言

轴流压气机失稳边界预测是叶轮机气动力学中最重要的问题之一，Emmons 等[1-7]通过大量试验研究和稳定性理论分析，建立了多种经验关联方法以判断压气机的稳定性，这些经典的判稳方法在现阶段研究中仍具有重要的借鉴意义[8-11]。其中，Koch 发展的最大静压升系数法基于压气机和扩压器相似的几何结构和流动特点，在对大量高、低速轴流压气机试验结果进行分析的基础上，提出将压气机级压升类比于二元扩压器扩压，该思想历经数年已被证明具有良好的普适性和可靠性。基于这种思想，Koch 将压气机失稳静压升系数归结为基元叶栅通道无量纲长度L/A2（叶栅通道扩张长度/出口宽度）的函数，再辅助以雷诺数、叶尖间隙和轴向间隙的修正系数，即可得到不同雷诺数、叶尖间隙和轴向间隙条件下的压气机失稳静压升系数[7]。因为具有简单便捷、关联参数较全面等优点，该方法已经得到广泛认可和应用。然而其中也存在一些问题，具体来说是在不同转速下压气机边界点压比预测值和试验值的误差有所不同，如文献[11]中4 级低速压气机的计算结果显示，边界点压比预测值和试验值的误差随转速提高而变大。由于不同转速代表不同的来流马赫数，推测这种边界点压比预测偏差是由马赫数的变化引起的。

关于马赫数对压气机失稳静压升能力及失稳边界预测的影响鲜见文献公开报道。为此，本文基于将压气机级压升类比于二元扩压器扩压的思想，在不同长宽比（扩张长度/进口宽度）和附面层堵塞程度下，开展马赫数对压气机失稳静压升系数影响的数值模拟研究。

1 数值模拟模型建立

1.1 计算模型和计算方法

二元扩压器模型如图1 所示。图中，扩压段进、出口位于站点1、2，A1、A2分别为进、出口宽度，L 为轴向扩压长度，θ 为半扩张角，x 为扩压段上游平行段长度，用于控制扩压段进口附面层堵塞程度的变化。计算平台为ANSYS FLUENT，湍流模型采用鲁棒性较好的S-A 模型，能较好地解决一些复杂流动，且计算时间较短[12]。计算模型进口给定总温、总压，出口给定均匀分布的静压。

进口马赫数Ma1通过调整背压大小来控制。考虑到本文计算中马赫数的最高取值达到0.73，流体可压缩性对失速静压升能力的影响不能忽略[13]，故静压升系数采用2 种定义

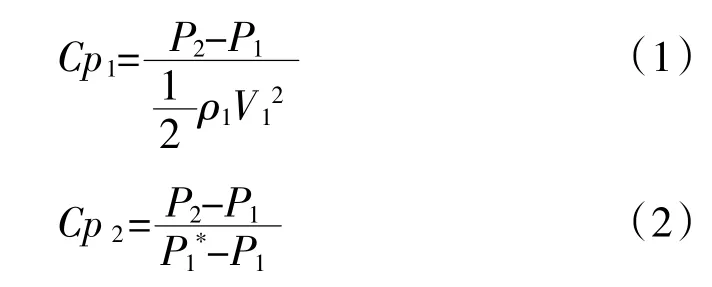
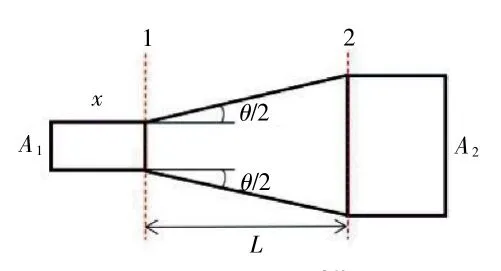
图1 扩压器模型

式中：P1、P2分别为扩压器进、出口静压；ρ1、V1分别为扩压器进口气流密度和速度；P1*为扩压器进口总压。根据定义，Cp2考虑了流体可压缩性，而Cp1没有考虑。2 种定义方式得到的失稳静压升系数受马赫数的影响将在后面作具体分析和比较。

1.2 计算方法验证

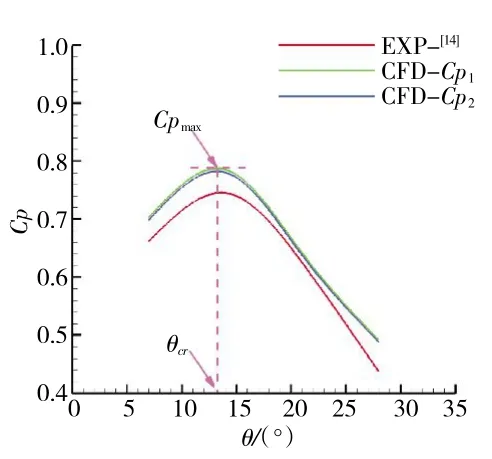
图2 计算结果与试验结果对比

为了验证上述计算方法对扩压器流场的适用性，根据文献[14]中给出的扩压器详细结构参数重新建模，并利用已经过无关性验证的网格进行计算。计算结果与试验结果对比如图2 所示。从图中可见，随着扩张角变大，静压升系数先增大后减小，在某一临界扩张角θcr压升曲线出现峰值（即达到Cpmax）。计算结果与试验结果在数值上最大仅相差4%（Cp1）和3.5%（Cp2），满足工程应用精度。总体来看，该计算方法可信度很高，可用于后续扩压器流场的数值模拟。

2 计算结果与分析

2.1 不同长宽比下马赫数的影响

以长宽比R=L/A1为参变量研究马赫数对失稳静压升系数的影响。选择长宽比做参变量是借鉴文献[14-16] 对扩压器静压升能力影响因素的研究思路，其范围的选择也不是任意的。文献[15]对长宽比处于1 个范围内的二元扩压器进行研究，发现过大的长宽比对提升静压升能力并没有好处。结合压气机叶片通道相关几何参数[7，16]，取长宽比为1.2、3.0、5.0，得到静压升系数随扩张角的变化，如图3 所示。从图中可见，在不同马赫数下，2 种定义方式得到的静压升系数变化规律基本一致；马赫数越大，二者的数值差距越大。在马赫数为0.10～0.51 的范围内临界扩张角基本相等，马赫数增大至0.73 时略有减小。

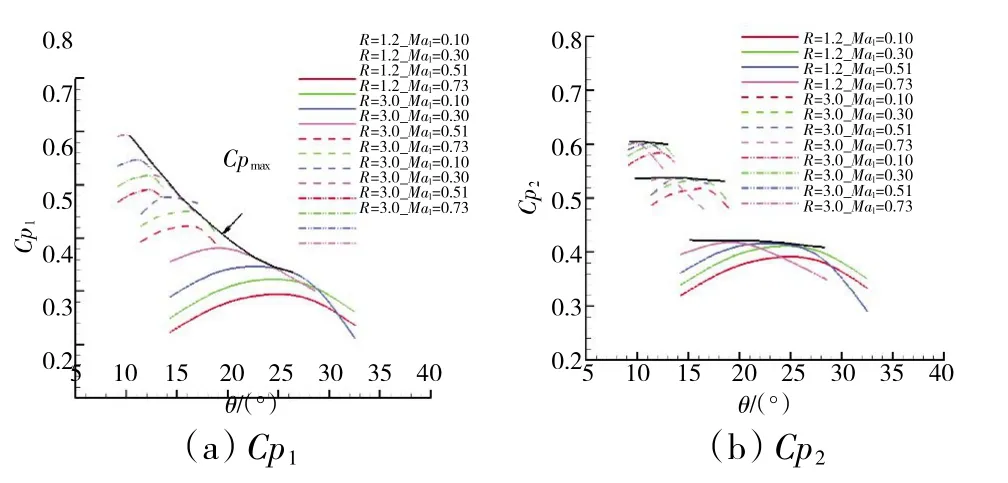
图3 不同长宽比下静压升系数随扩张角的变化

马赫数和长宽比对失稳静压升系数的影响是相互独立的，如图4 所示。对未考虑流体可压缩性的静压升定义Cp1，增大马赫数和长宽比均有利于失稳静压升系数的增大；对考虑了流体可压缩性的静压升定义Cp2，增大长宽比，失稳静压升系数随之增大，但马赫数从0.10 增大到0.73 的过程中，失稳静压升系数变化很小，增大幅度不超过2.5%。

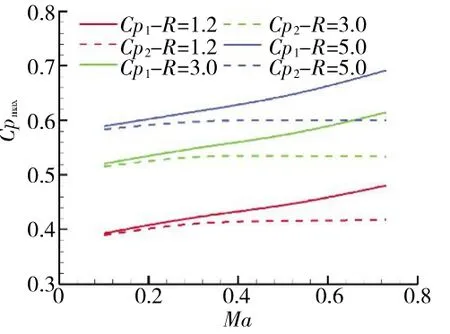
图4 不同长宽比下失稳静压升系数随马赫数的变化

根据文献[7]将失稳静压升系数归结为无量纲长度的函数的思想，由于

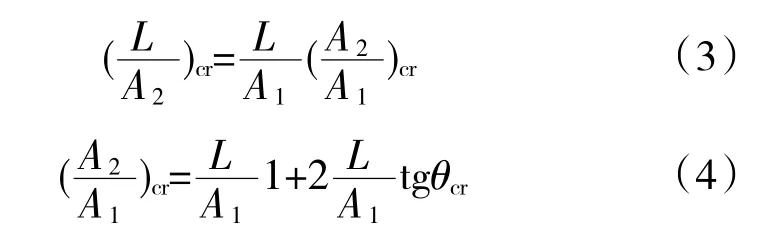
若忽略马赫数对临界扩张角θcr的影响，不难得知在（L/A2，Cp2max）坐标系中，长宽比相同、马赫数不同的各点重合，长宽比不同、马赫数相同的各点连线（即关联曲线）也重合。利用同样的处理方式在（L/A2，Cp1max）坐标系中得到不同马赫数下的关联曲线走势相同但位置不同。这一结果表明，如果在静压升系数定义中不考虑流体可压缩性，为了提高压气机失稳边界预测的准确度，在不同马赫数下需要利用不同的关联曲线进行预测，或者添加马赫数修正系数；相反，如果在静压升系数定义中考虑流体可压缩性，便可以忽略马赫数的修正，在大范围马赫数下都能运用同一条关联曲线进行压气机失稳边界预测，预测过程相对简化。

2.2 不同附面层堵塞程度下马赫数的影响

以附面层堵塞程度即上游平行段长度为参变量研究马赫数对失稳静压升系数的影响。以长宽比R=3 为例，取平行段长度x=0.5、1.5、2.5、3.0 m，对应的扩压段进口附面层堵塞程度如图5 所示。无量纲位移厚度2δ*/A1表征附面层堵塞程度，其中

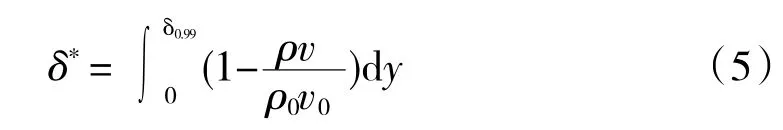
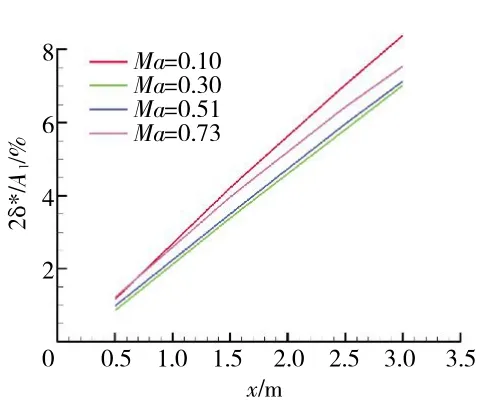
图5 附面层无量纲位移厚度随平行段长度的变化

式中：ρ、v 分别为扩压段进口截面沿宽度方向各点的密度、速度；ρ0、v0分别为扩压段进口截面中心的密度、速度。

2δ*/A1越大表示进口附面层堵塞程度越高。从图中可见，当平行段长度从0.5 m 加长到3.0 m 时，附面层堵塞程度越来越高，在不同马赫数下附面层堵塞程度差别不大。

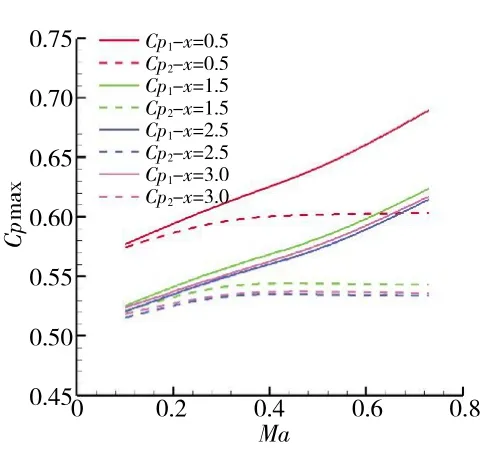
图6 不同平行段长度下失稳静压升系数随马赫数的变化

马赫数和附面层堵塞对失稳静压升系数的影响也是基本独立的，如图6所示。从图中可见，随着平行段的加长，附面层堵塞程度变高，整体上失稳静压升系数呈减小的趋势，这一结果与常规认识是相符的[17-18]，且与第2.1 节的结果一致，马赫数对失稳静压升的影响与静压升系数定义方式有关。若静压升系数定义考虑了流体可压缩性，在大范围马赫数下都能运用同一条关联曲线进行压气机失稳边界的预测，预测过程相对简化。

2.3 失稳静压升系数与无量纲长度关联曲线

在不同马赫数下失稳静压升系数与无量纲长度关联曲线如图7 所示。将文献[7]中的二元扩压器（黑色曲线）和一些压气机（黑色圆点）的失稳静压升数据也一并绘于图中。从图中可见，计算所得关联曲线的变化趋势与文献关联曲线的基本一致，但相对位置均有所偏高。考虑到计算方法本身的误差（图2），计算结果的可靠性还是值得肯定的，可以作相应的定性分析。

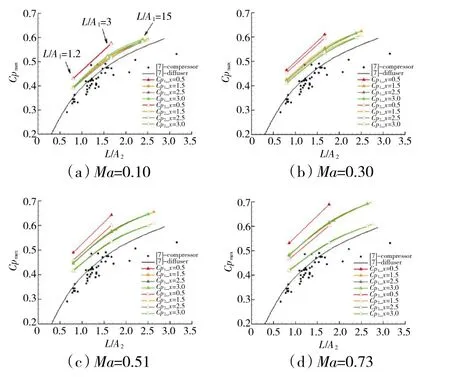
图7 失稳静压升系数与无量纲长度关联曲线

对于不同的静压升系数定义方式，由于Cp2max＜Cp1max，Cp2max对应的计算关联曲线与文献数据更吻合。对于不同的平行段长度，当x=1.5、2.5、3.0 m 时,计算关联曲线与文献数据更吻合，且3 种平行段长度的关联曲线基本重合，此时附面层无量纲位移厚度为4.5%～7.0%。

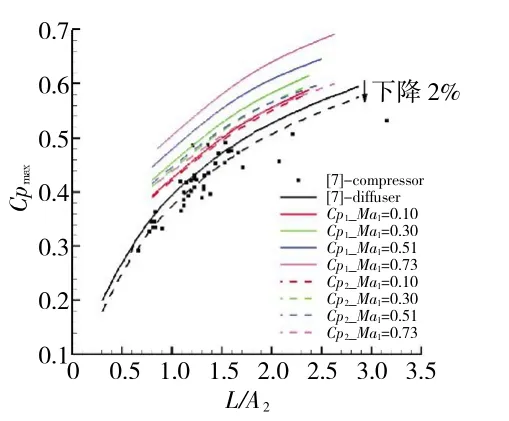
图8 平行段长度为2.5 m 时失稳静压升系数与无量纲长度关联曲线

对于不同的马赫数，其关联曲线位置与静压升系数定义方式关系密切，如图8 所示。从图中可见，以平行段长度为2.5 m 时为例，对于Cp1max，马赫数越小，计算关联曲线与文献数据越吻合；Cp2max对应的计算关联曲线与文献数据的吻合度比Cp1max更高，且在不同马赫数下的关联曲线几乎重合。若将文献中的关联曲线降低2%作为相对更符合压气机失稳静压升系数的关联曲线（即黑色虚线），不难看出Cp2max所在关联曲线与黑色虚线最高仅相差5%。考虑到计算方法本身的误差，其准确度还是比较高的。这一结果更直观地证实了前面“可以忽略马赫数对考虑了流体可压缩性的失稳静压升系数的影响，从而简化压气机失稳边界预测过程”的结论。