循环热载荷下CMAS 侵蚀对EB-PVD 热障涂层微裂纹特性的影响

王 婕

（中国航空发动机研究院，北京100097）

0 引言

热障涂层（Thermal Barrier Coating，TBC）广泛用于航空发动机热端部件[1]，包括高温合金基底、陶瓷顶层（Top Coat，TC）、黏结层（Bond Coat，BC），以及生长氧化物层（Thermally Grown Oxide，TGO）。TBC 通常采用7%～8%氧化钇部分稳定氧化锆（Yttria stabilized zirconia，YSZ），耐热腐蚀性好、熔点高、导热系数小，热膨胀系数较大[2]。TBC 制备工艺主要包括大气等离子喷涂（Atmospheric Plasma Spray，APS）和电子束物理气相沉积（Electron Beam-Physical Vapor Deposition，EB-PVD）[3]。

钙镁铝硅酸盐（Calcium-Magnesium -Alumino-Silicate，CMAS）侵蚀是影响TBC 的关键因素之一[4]。服役环境下，CMAS 与火山灰、粉煤灰等进入发动机并沉积在叶片上。当柱状晶表面温度超过CMAS 熔点时，发生CMAS 熔融浸入TBC 空隙。由于黏性阻力的增大，CMAS 侵蚀率会随着厚度增加而逐渐降低[5]，CMAS 温度随进入TC 层的深度增加而逐渐降低[6-7]。为减轻CMAS 侵蚀影响，国内外开展了大量研究。研究表明，侵蚀过程中产生了新的结晶形态，如钙长石（CaAl2Si2O8）[8]、磷灰石（Ga2Gd8（SiO4）6O2）[4]，以及石榴石类型晶体[6]。新的结晶会阻止CMAS 侵蚀，但也会导致涂层丧失其多孔特征。此外，TC 层的化学成分、温度梯度和CMAS 的硬化也是影响CMAS 侵蚀的重要因素。冰岛埃亚菲亚德拉火山喷发事故使得火山灰的问题受起了极大关注[9]。火山灰黏附在涂层表面形成CMAS，在高温下迅速侵入TC 层间隙。冷却凝固时，导致侵蚀层具有较高的模量和导热性[10]，且会引起热失配，使涂层应变韧性变差，导致裂纹萌生、扩展，引起涂层剥落失效[11]。了解CMAS 侵蚀过程中的涂层断裂失效机制至关重要。Chen[12]指出CMAS 的热弹性特性显著影响界面脱层的能量释放率；Su 等[13]发现面内模量降低会增大应变能释放率；Zhang 等[14]研究了CMAS 引起的瞬态热应力。当前，热循环载荷作用下的研究多集中在TGO 生长[15]、裂纹扩展[16]、均匀温度场的裂纹竞争等[17]方面，只有少数考虑了CMAS 渗滤过程对微观结构和非均匀温度分布的影响[18-19]。因此，亟需开展热循环载荷环境下CMAS 侵蚀行为对TBCs 微观结构及性能影响的研究。

本文建立温度梯度下CMAS 侵蚀EB-PVDTBC的数值分析模型，并通过温度场、应力场和能量释放率定量描述CMAS侵蚀对TBC 的影响规律。

1 数值模型

1.1 有限元模型

本文选用有限元软件ABAQUS 6.14 进行数值分析。含裂纹EB-PVD TBCs 微观结构的2 维平面模型如图1 所示。EB-PVD 涂层的高孔隙率间隙为主裂纹，其余裂纹视为微裂纹。所建立的有限元模型包括11 个含间隙的YSZ 柱状晶，从左至右以此编号为#1～#11；其中柱状晶宽度和间隙宽度分别记为D 和d。考虑到实际制备的TC 孔隙率约为10%[20-22]，在本文模型中假设YSZ 柱宽D=9 μm，高孔隙率氧化间隙宽度d=1 μm。HTC、HBC和HSUB分别为TC、BC 和基底层的厚度。HCMAS0 为TC 层顶部以上的沉积高度，HCMAS为CMAS 侵蚀EB-PVD 体系柱间隙的深度。假定基底的厚度HSUB=300 mm，并选择HTC=HBC=100 μm[3]，HCMAS0=20 μm[11]。此外，考虑了长度为2a 的裂纹，裂纹深度定义为从CMAS0/TC 界面到裂纹中心的距离HCRACK（图1）。

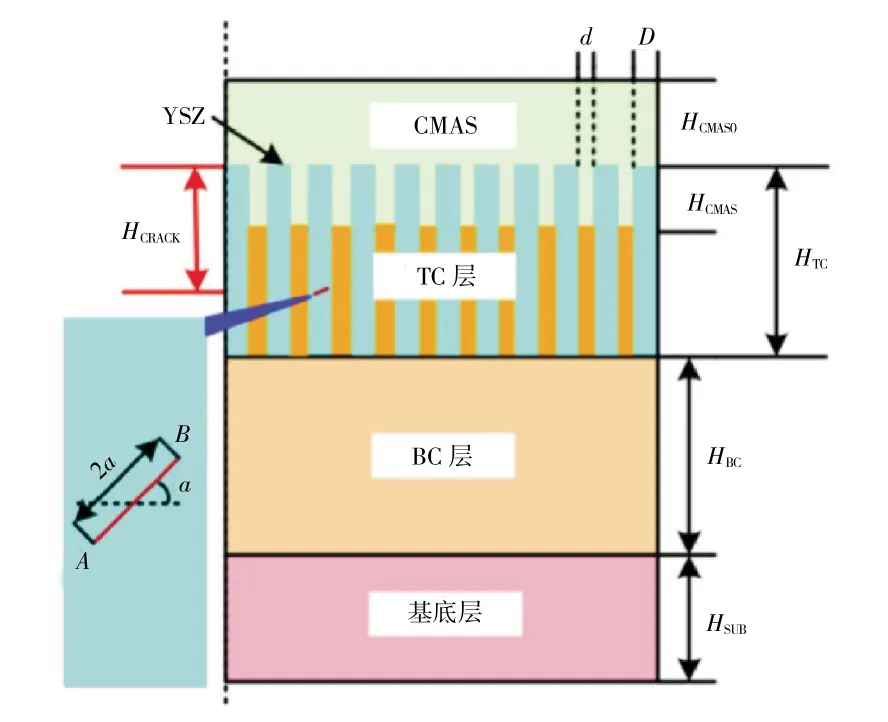
图1 CMAS 侵蚀EB-PVD 热障涂层系统

1.2 材料参数

本文所建立的有限元模型包括约45000 个4 节点四边形单元（热传导分析为DC2D4，热应力分析为CPE4R）。靠近裂纹尖端和YSZ/CMAS/高孔隙率氧化界面采用更为精细的网格捕捉奇异点，并开展网格敏感性分析，以保持计算的收敛性[23]。为了进行热应力分析，将温度场作为预定义场，采用传热程序模拟了3 个热循环过程中的瞬态温度场。

本文假定高温下TBCs 杨氏模量、泊松比和热膨胀系数等为黏弹性，密度、导热系数和比热容为常数。TBCs 各层的温度相关材料参数见表1。需要强调的是，所选的温度相关的高孔隙率氧化物的材料具有相对较小的杨氏模量和热传递系数。

1.3 载荷及边界条件

考虑到研究对象的对称特性，数值模型采用半周期几何模型，数值模型左侧设置为对称边界条件，右侧设置为周期性边界条件（图1）。模型的左侧边界不允许沿水平方向移动，右侧边界可自由移动，但右侧边界上所有节点的水平位移约束一致。CMAS 的上边缘不受任何约束。为了忽略模型中的弯矩，底部边缘固定在垂直方向。同时，假设裂纹表面自由且与热流绝热。

所施加的热载荷历程曲线如图2 所示。在每个热循环中，TBCs 的温度场都是随时间变化的。假设TBCs 在20 ℃下为无初始应力状态。在300 s 内将CMAS 顶部从20 ℃加热到TCMAS的1100 ℃，将基板底部从20 ℃加热到TSUB的800 ℃。恒定高温保持14400 s，以模拟CMAS 侵蚀过程。然后，在300 s 内将TBCs 冷却到20℃。为了考虑传热的影响，采用加热、保温和冷却过程来确定每个热循环的瞬态热负荷条件。

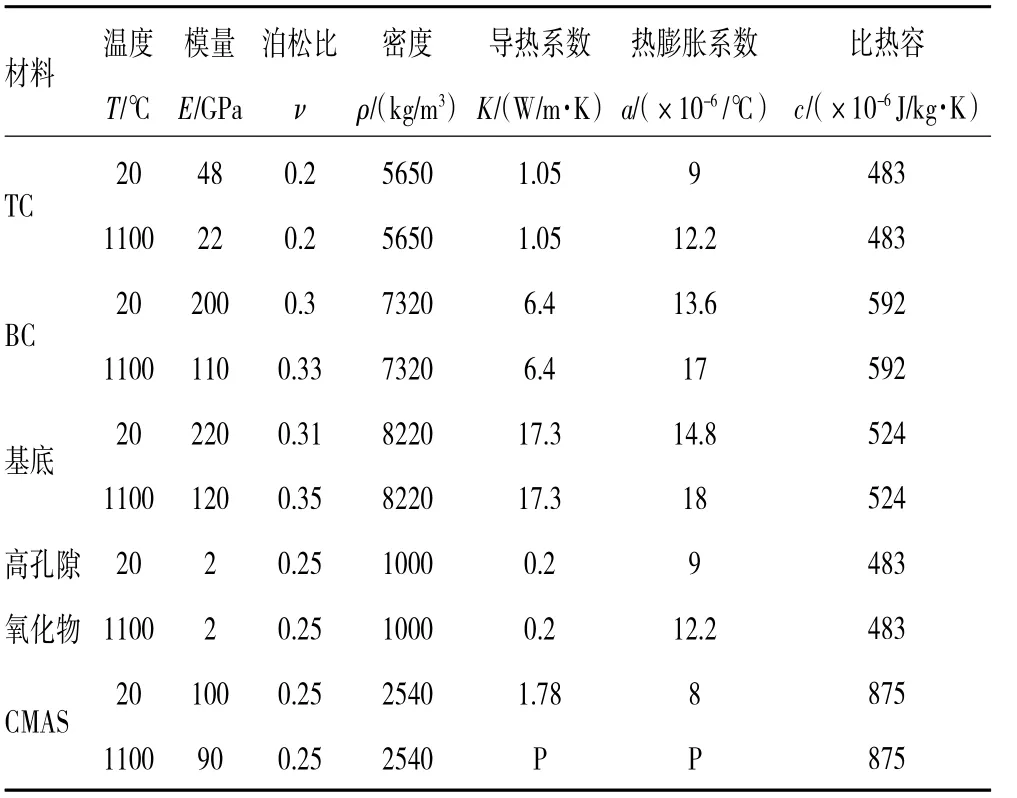
表1 TBCs、CMAS 和多孔氧化物的材料性能参数[19，24-28]

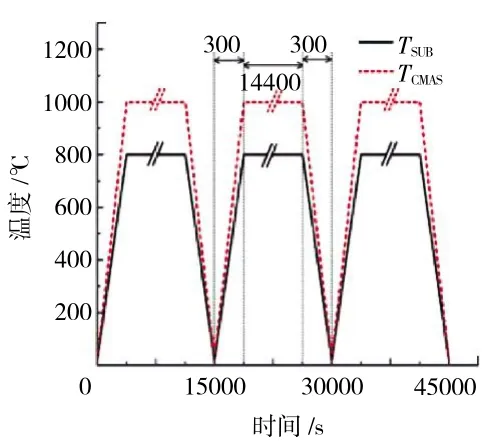
图2 热障涂层系统的热载荷时程曲线

1.4 CMAS 侵蚀

假设初始阶段YSZ 柱状晶之间存在一定的空隙。随后，沉积的CMAS 在毛细作用下侵蚀到空隙中。Naraparaj 等[6]采用2 种真实的火山灰和1 种合成的CMAS 粉末试验确定了CMAS 侵蚀的材料特性，为化学反应形成结晶相阻止熔融玻璃相的侵蚀分析提供了1 种有效手段。本文根据该试验结果[6]，对CMAS材料数据进行拟合，得到的拟合曲线如图3 所示，用以评估侵蚀深度HCMAS（t）随时间的变化为

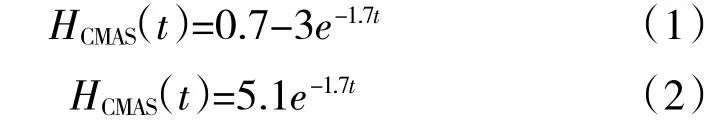
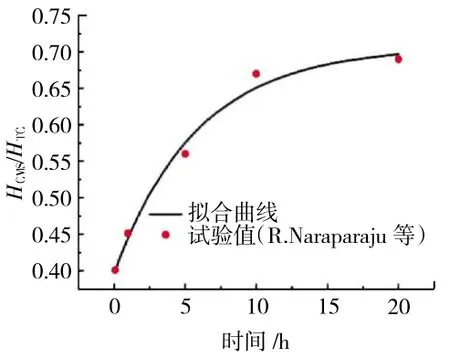
图3 侵蚀深度随服役时间变化

式（2）即为CMAS 侵蚀率表达式。需要强调的是，侵蚀深度与侵蚀时间关系反映了温度分布和化学反应的情况。本文采用ABAQUS 中的“depvar”（指定与解决方案相关的状态变量的编号）和“User defined field”（为用户子程序USDFLD 更新材料点的场变量）模拟CMAS 侵蚀过程，这使得能够将材料特性从高孔隙率氧化转移到以式（2）所定义的侵蚀率来模拟CMAS 侵蚀过程。

2 结果与讨论

2.1 温度场分布

在高温保温过程中，温度为800～1100 ℃，如图4 所示。

需要注意的是，TC 层的热导率（1.05 W/m·K）在TBCs 系统中是最低的，提供了将近150 ℃的隔热效果。在高温过程中（忽略加热和冷却过程）具有不同CMAS 热导率的TC 层隔热性能如图5 所示。图中温差代表了TC 顶部界面（CMAS0/TC）与TC/BC 界面之间的温度差。HCRACK=65 μm，且，并在图1 中#6 柱状晶HCRACK=65 μm 的位置处预置1 条长度为4 μm 的裂纹。结果表明，较高的CMAS 热导率会降低TC 层的隔热性能；随着CMAS 热导率提高，CMAS 侵蚀高孔隙率氧化物更加有损于涂层的隔热性能[23]。

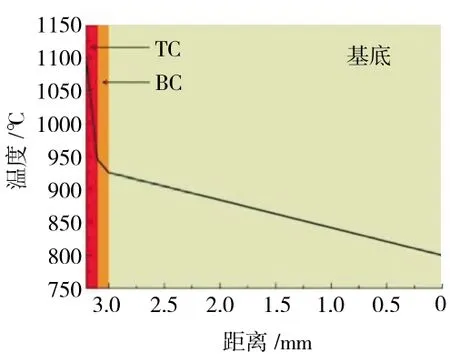
图4 400 s 时涂层系统的温度

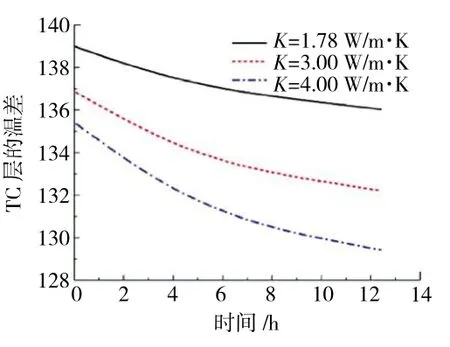
图5 不同CMAS 热导率下陶瓷层隔热效果

在高温过程中不同角度微裂纹附近的温度和热流分布如图6 所示。从图中可见，在裂纹倾角α＝0°时，裂纹尖端附近存在1 个较大的温度梯度，且垂直裂纹不会影响温度分布。在CMAS 侵蚀过程中不同角度裂纹右端裂尖区域的归一化热流分布如图7 所示。其中归一化数值为裂纹倾角α＝0°时的热流值。结果表明，随着裂纹倾角的增大，热流密度逐渐减小。在此阶段CMAS 开始到达微裂纹，在第2 次热循环加载期间热通量逐渐减小。另外，由于垂直裂纹基本不会阻塞热流路径，因此垂直裂纹的热通量与没有裂纹时的基本相同。基于以上讨论可以发现，温度和热通量场明显受到微裂纹的倾角和侵蚀深度的影响。

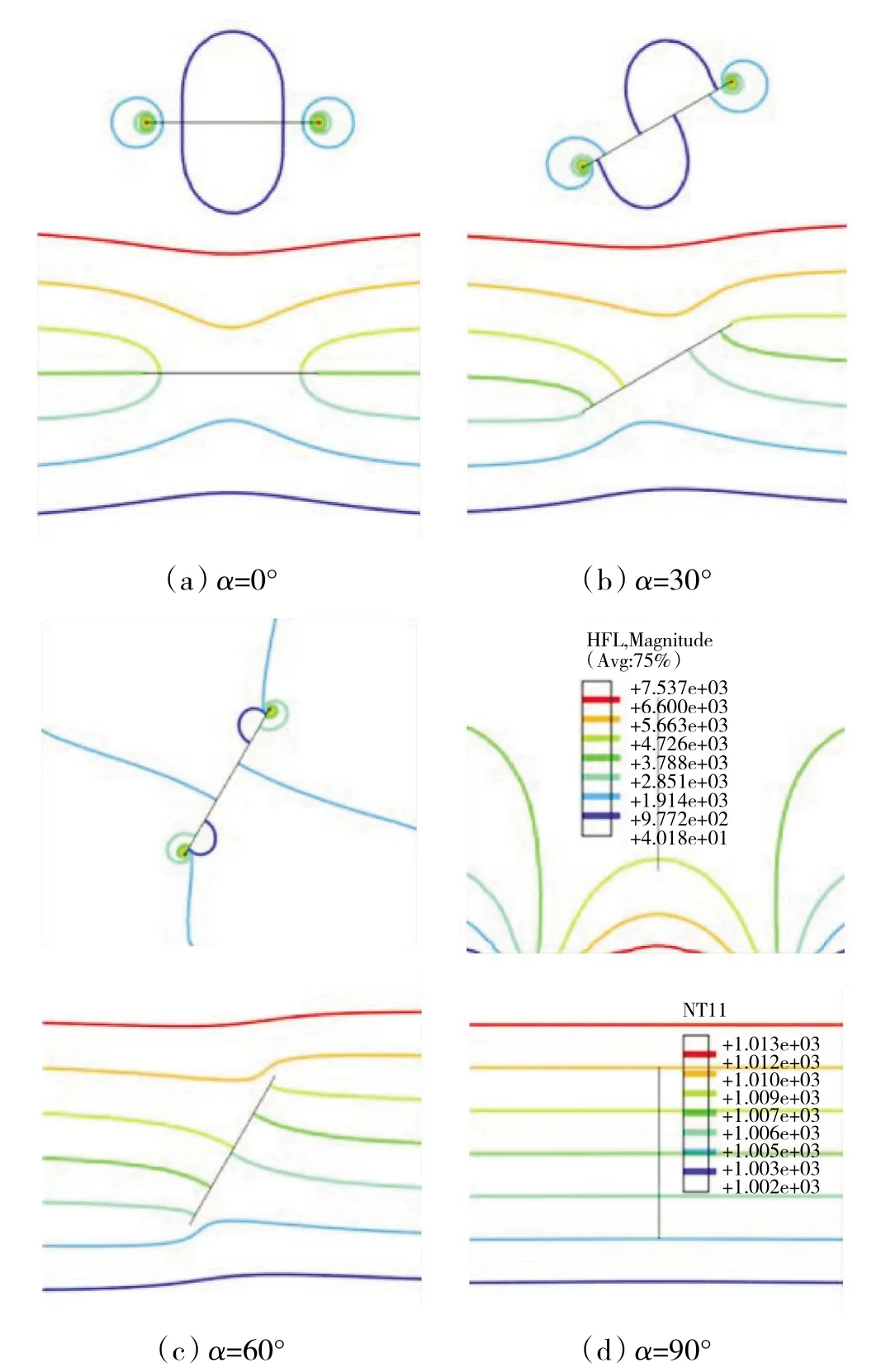
图6 在不同裂纹倾角下陶瓷层内热流和温度

2.2 应力场分布

图7 在CMAS 侵蚀中不同裂纹倾角下裂尖处热流

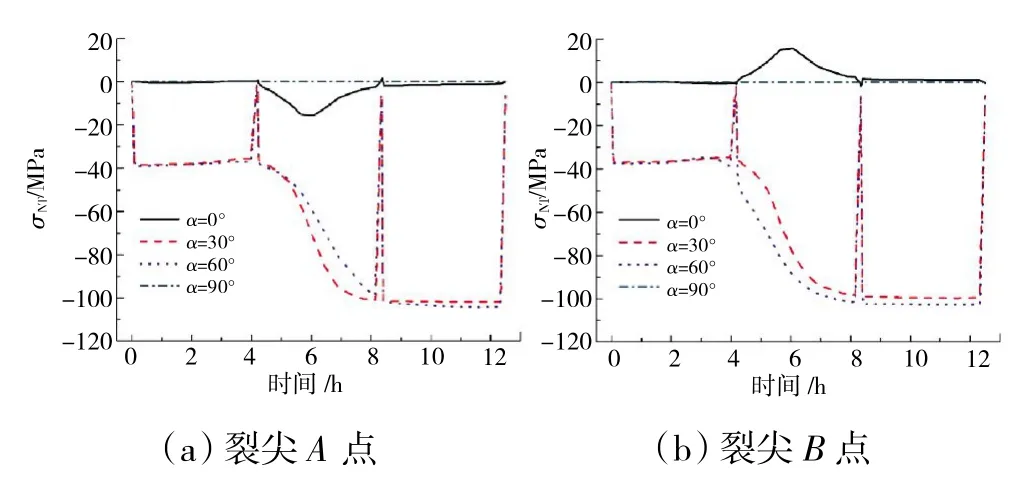
图9 在CMAS 侵蚀过程中不同裂纹倾角下裂纹尖端附近的滑移型应力

本节主要分析在CMAS 侵蚀过程中微裂纹尖端的张开型应力（垂直于裂纹平面的拉伸应力）和滑移型应力（平行于裂纹平面的剪应力）的变化。当微裂纹嵌入#6柱（HCRACK=65 μm）时，不同裂纹倾角下微裂纹尖端处的张开型应力和滑移型应力大小分别如图8、9 所示。其 中，HCRACK=65 μm，αCMAS=8.5 ×10-6℃，KCMAS=1.78 W/m·K。从图中可见，应力随加热时间的延长而增大，随冷却时间的延长而减小。在第2 次热循环加载过程中，当CMAS 到达微裂纹处时，应力出现剧烈振荡现象。CMAS 侵蚀对应力的影响可分为3 个阶段。第1阶 段：微 裂 纹（HCRACK=65 μm） 远 离CMAS 时（HCMAS=40～55 μm），微裂纹周围的应力场基本不受CMAS 的影响，应力相对较小且趋于稳定；第2 阶段：CMAS 接近微裂纹时（HCMAS=55～63 μm），由于CMAS对环境的剧烈转换，应力逐渐增大，此时，渗入的CMAS 熔体将凝固并占据EB-PVD 柱间的空隙，导致应变容限和分层严重退化，并导致微裂纹扩展；第3阶段：微裂纹（HCRACK=65 μm）被CMAS 完全或部分覆盖时（HCMAS=63-67 μm），应力持续稳定在一个较高的水平。此外，当微裂纹的倾斜角度为60°或90°时，微裂纹近似表现为张开型断裂，如图8 所示。当微裂纹的倾斜角度为30°或60°时，微裂纹表现为滑移型断裂（图9）。值得注意的是，在第2 热循环加载期间，在α=30°时裂尖A 点处的滑移型应力值大于在α=60°时的值（图9（a））；然而，在图9（b）中，在α=30°时裂尖B点处的滑移型应力的值小于α=60°时的值。这是由于裂纹尖端与CMAS 之间的距离不同造成的。图9（b）表明，在α=60°时，裂尖B 点周围的滑移型应力大于在α=30°时的值。这是因为在α=60°时裂尖B 点和CMAS 之间的距离小于在30°时裂尖B 点和CMAS之间的距离。与之相反，在α=60°时，裂尖A 点与CMAS 之间的距离大于在α=30°时裂尖A 点与CMAS之间的距离。此外，CMAS 侵蚀对水平裂纹的张开型应力和滑移型应力影响较小。综上所述，CMAS 侵蚀对裂纹尖端应力状态有显著影响，且与裂纹角度明显相关。

2.3 能量释放率

当能量释放率（Energy Release Rate，ERR）G 的最大值超过其临界值时，微裂纹开始扩展，导致YSZ柱状晶局部失效，从而导致陶瓷涂层最终剥落。本节中所有G 的结果均由参考值GMAX 标准化。由于裂纹尖端A 与B 变化趋势相似，本节将重点讨论尖端A 的变化情况。

在不同倾斜角下G 随渗透时间的变化趋势如图10（a）所示。当CMAS 到达微裂纹时，张开型应力和滑移型应力都会急剧增大。因此，G 在第2 热循环中迅速增大。随着倾斜角度的增大，尖端A 的G 单调增大。下面仅讨论微裂纹倾斜角为60°的情况。在CMAS渗透过程中，CMAS 的热膨胀系数对高温下G 的影响如图10（b）所示。需要注意的是，高温下CMAS 的热膨胀系数减小会导致裂纹扩展驱动力显著增大。热失配应力的增大将促使裂纹分层。CMAS 和TC 层之间的热膨胀失配越大，YSZ 柱层中的G 值越大，从而导致微裂纹扩展。裂纹高度对G 的影响如图10（c）所示。对于不同的裂纹高度，由于CMAS 到达裂纹的时间不同，G 值急剧增大的发生时间也有所不同。例如，当裂纹高度为52、60 和68 μm 时，G 值急剧增大分别发生在第1、2、3 个热循环。为考虑YSZ 柱状晶中有多个微裂纹的情况（如图10（d）所示），描述了微裂纹密度对G 的影响。这里考虑3 种不同的情况：第1种是对于位于＃6 柱状晶的裂纹，裂纹数量NCRACK=1；第2 种是分别位于#3，#6 和#9 柱状晶的裂纹，数量NCRACK=3；第3 种是分别位于#2，#4，#6，#8 和#10 柱状晶的裂纹，数量NCRACK=5。结果表明，裂纹数量为3和5 时的G 均小于裂纹数量为1 时的。这意味着可以通过增加微裂纹密度来降低微裂纹急剧扩展的可能性。

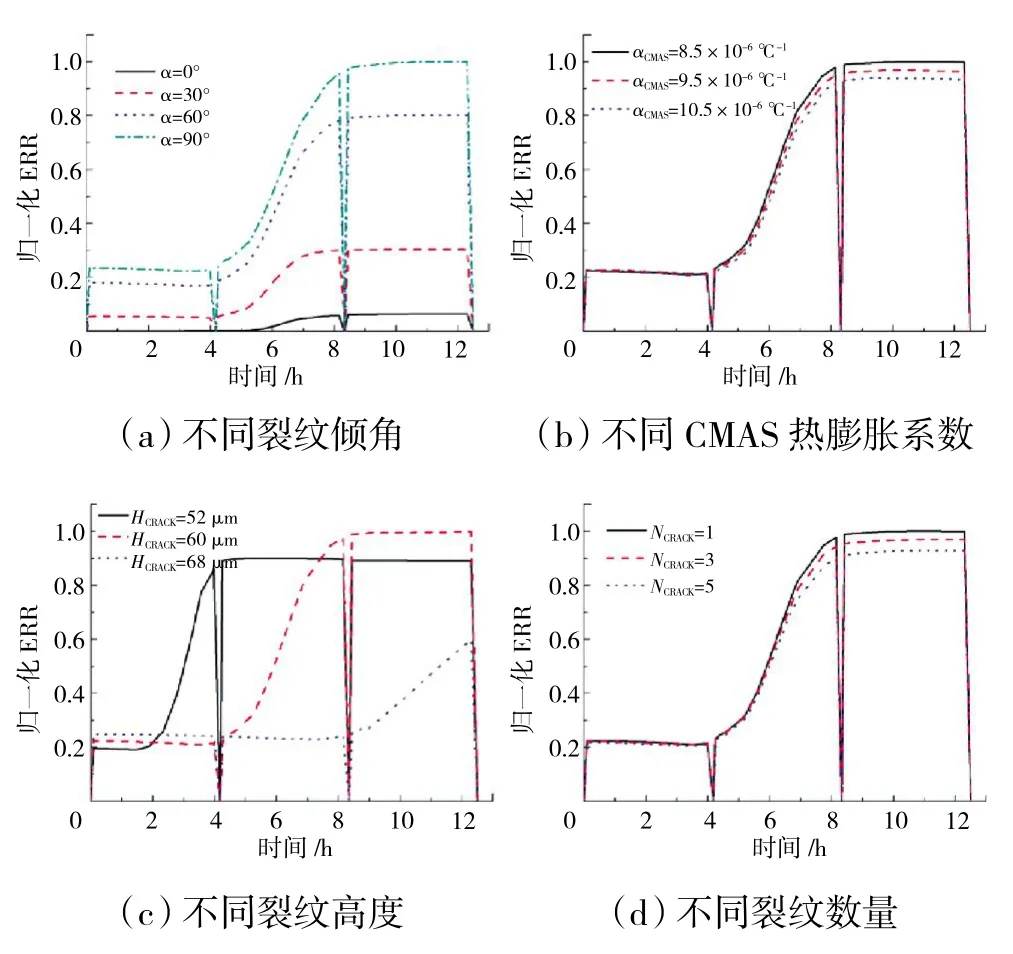
图10 不同工况下裂纹尖端A 的归一化能量释放率

3 结论

本文建立了柱状晶中含微裂纹的EB-PVD TBC系统数值模型，研究了CMAS 侵蚀对EB-PVDTBC 隔热性能、裂纹周围温度场与应力场以及能量释放率分布的影响规律，得到以下结论：

（1）CMAS 的导热系数、热膨胀系数、微裂纹位置和密度等对陶瓷层的温度场及隔热效果有重要影响；

（2）当CMAS 侵蚀到达微裂纹时，微裂纹附近的应力水平和能量释放速率都急剧增大。随着服役时间的延长，CMAS 侵蚀会严重降低TBC 隔热性能，并引起较大的应力，容易导致涂层剥落失效；

（3）CMAS 侵蚀对裂纹尖端的温度场、应力场以及能量释放率的影响程度与裂纹倾角显著相关，其影响可以分为3 个显著不同的阶段。