基于数值模拟的流场附面层边缘识别方法
2021-04-06张堃元司江涛刘凯礼蔡北京杨心宇
王 磊 张堃元 司江涛 刘凯礼 蔡北京 杨心宇
(1.上海飞机设计研究院,上海 201210;2.南京航空航天大学,南京 210016)
0 引言
附面层是壁面附近流动因黏性而受阻滞的一部分区域,其边缘通常取在速度达到主流0.99倍的位置。对附面层的研究是进气道、喷管、机翼等内外流流场设计中的重要内容,例如对无黏设计结果进行黏性修正、分析附面层对主流的影响、判断流动是否有分离的趋势等。获取附面层厚度以及附面层内参数分布是进行这些研究的基础。
工程设计中有一些简单的经验公式可用于估算附面层的发展。例如,文献[1-4]计算喷管附面层位移厚度δ1采用发展长度x的线性函数:
δ1=xtanβ
(1)
其中,角度β与喷管出口马赫数有关;文献[5-6]根据公式(2)计算高超声速进气道附面层位移厚度:
δ1=Ax+Bxe-x
(2)
其中,A、B为根据经验确定的系数;文献[7]中应用了一种形式更复杂的经验公式。这些公式计算量小、使用方便,但显然其计算精度以及能够获取的信息是比较有限的。
求解附面层方程是较为传统的附面层近似计算方法。其中多数是对附面层动量积分方程补充经验关系式后求解,例如文献[8-11]在进气道、喷管、叶栅等流道设计的黏性修正中应用的方法。也有些直接针对附面层偏微分方程组进行数值计算,例如Cebeci[12]、杜国樑[13]所提出的方法,其中Cebeci提供的计算程序在许多进气道、喷管设计中得到应用[14-18]。
随着CFD技术的飞速发展,基于黏性N-S方程组的数值模拟已得到普遍应用,与上述两种方法相比,其精度更高,适应性更广。但N-S方程组求解中一般不特意区分附面层与主流,这使得如何在流场数据中准确认定附面层边缘成了新的问题。按照通常的定义,附面层边缘取在速度达到主流0.99倍的位置,而在较复杂的流场中主流本身并不均匀,因此需要根据经验人为给定主流速度的数值[19-21],有较大的主观性并且难以实现自动化识别;有文献中根据附面层和主流中法向速度梯度大小的差异判断附面层边缘[22],也存在类似的问题。
针对在流场数值计算结果中识别附面层的困难之处,本文根据附面层的概念,提出以排除了附面层干扰的“参考主流流场”中的速度代替实际流动主流速度确定附面层边缘的方法,以典型的超声速压缩型面为例对该识别方法进行了验证,并根据识别结果考察了应用附面层修正的设计效果。
1 附面层边缘识别方法
针对在流场数值计算结果中识别附面层的困难之处,本文根据附面层的概念,提出以排除了附面层干扰的“参考主流流场”中的速度代替实际流动主流速度确定附面层边缘的方法,并以超声速压缩型面为例对该识别方法进行了验证。
如引言所述,根据数值模拟结果识别附面层困难之处在于复杂流场中主流速度的确定,主流应是附面层外、没有受到壁面与流体之间剪切力影响的流动。满足这种要求的流场通过零剪切滑移壁面条件下的数值模拟可以获得,这里称之为“参考主流”,其中流动没有附面层,完全排除了壁面与流体之间剪切力的影响。
在流场中黏性相互作用较弱时(对其强弱的判断参见文献[23]的说明),可以认为实际流动中主流流动与这种参考主流相同。因此根据附面层的定义判断其边缘时,可以用这种参考主流中对应位置的速度代替所需的实际流场主流速度,这种方法避免了人为指定主流速度的主观性,因而更为科学合理,也有利于识别过程的自动化。
图1为该方法识别过程的示意图。在壁面上的指定位置(例如图1中x)建立沿壁面法向的单位向量n和沿壁面切向的单位向量s,沿向量n方向新建一系列网格点,依次验证各点参数是否满足公式(3):

图1 附面层边缘识别过程示意图
(V-0.99Vref)·s≥0
(3)
式中,Vref为上述参考主流中该网格点的速度向量,V为实际流动中的速度向量(可以是数值计算或实验测量的结果),第一个满足该式的点即判定为该截面附面层边缘。对于壁面所有位置重复该过程,能够获取一系列边缘点,依次连接就得到了整个壁面上的附面层边缘曲线。
值得说明的是,对于主流湍流度较小并且不存在强剪切的流动,也可以用无黏条件下的模拟结果近似代替滑移壁面条件下的计算作为参考主流,这有利于减小计算量。
本文在商业软件ANSYS FLUENT的Scheme语言环境中编制了能够自动完成整个计算和识别过程的程序。
2 流场数值模拟方法及算例校验
本文研究中采用软件ANSYS FLUENT进行数值模拟,首先利用文献[24-25]中超声速压缩拐角的实验结果考核了所采用的软件和算法对超声速流动中附面层计算的可靠性。
图2为该实验模型的示意图。风洞实验段尺寸203 mm×203 mm,来流马赫数2.87,总压0.68 MPa,总温282 K,实验模型为8°的斜楔,模型宽度152 mm,贴于风洞底面安装,斜楔拐角距离喷管出口1.2 m。实验采集了压缩拐角前后若干截面上的参数分布,本文采用了拐角前25.4 mm(记为截面1)和拐角后66.04 mm(记为截面2)两个垂直于壁面的截面上时均速度分布。实验的其他数据见文献[25]。
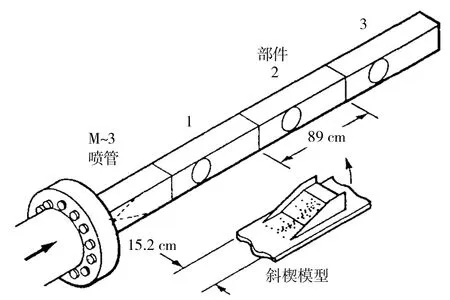
图2 实验模型示意图[24]
针对该实验进行了二维数值计算。计算模型参考了文献[26-27]的做法,在截面1前补充长度为2.0 m的附面层发展平板以保证截面1附面层速度分布与实验相同,图3为计算模型示意图。计算的总网格量约400 000,壁面y+约25。进口边界条件为压力远场,出口为压力出口,壁面为绝热无滑移固壁边界。
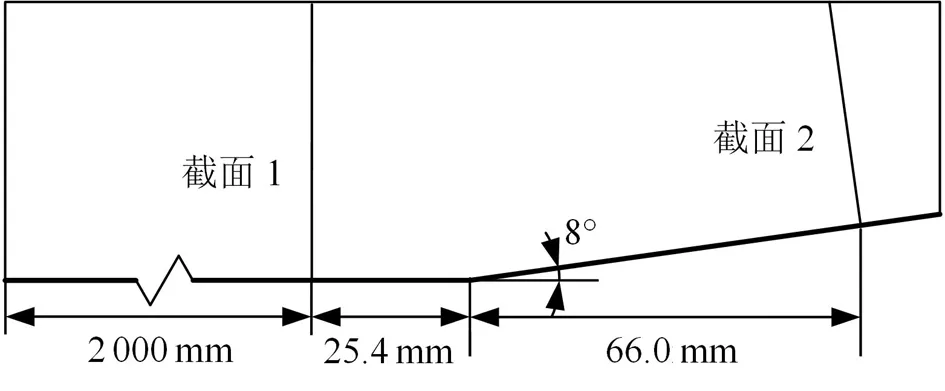
图3 计算模型示意图[24]
采用基于密度的耦合隐式算法求解RANS方程,对流通量采用基于二阶迎风格式的AUSM方法计算。湍流模型选用标准k-ε模型,采用二阶迎风格式离散,近壁采用标准壁面函数处理。比热比取定值1.4,黏性系数采用Sutherland公式计算。以来流条件初始化开始计算,当各项残差不再下降并且进出口流量相对误差低于10-3时完成计算。
图4显示了截面1和截面2速度分布的实验与计算结果,图中η为沿壁面法向的坐标,uξ为平行于壁面方向的速度大小。其中截面1计算与实验最大误差为5.5%,均方根误差0.35%,表明拐角前来流满足实验条件;截面2计算结果与实验相吻合,速度最大误差为4.4%,均方根误差0.27%,表明所采用的计算方法是可靠的,后续研究中均采用类似的算法进行计算。
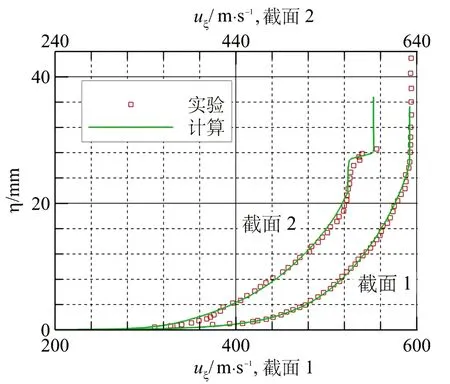
图4 两个截面上速度分布的实验和计算结果
3 附面层识别方法的验证
取来流条件为:M=6,p=2 511 Pa,T=221.6 K,在无黏条件下设计了以下两种超声速压缩型面:
1)三级斜楔压缩型面:三个压缩角分别为5.07°、5.71°和6.47°,无黏情况下三道激波汇聚点距离型面前缘高度为100 mm,壁面长度为433 mm;
2)弯曲压缩型面:根据压力分布反设计得到,设计方法参见文献[28],无黏情况下激波高度100 mm,壁面长度L=394.5 mm,壁面压力分布为分段函数:
(4)
其中,下标i为分段节点序号,p1/p=1.67,式中其他参数取值见表1。
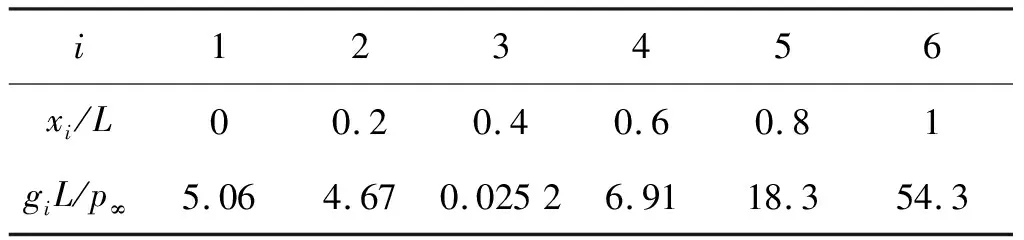
表1 壁面压力分布函数中的参数取值
对这两个压缩型面进行数值模拟得到流场参数,计算中来流湍流度为1%,来流湍流黏性与分子黏性之比为1。之后对两个压缩型面进行无黏计算作为参考主流,应用第1节所述识别算法提取了附面层边缘。
图5显示了两个压缩流场的马赫数等值线以及提取出的附面层边缘曲线。从图中可见,除有激波穿过的局部范围外,所提取的边缘曲线光滑连续,均位于速度急剧变化区域的外缘,与附面层的物理意义相符。
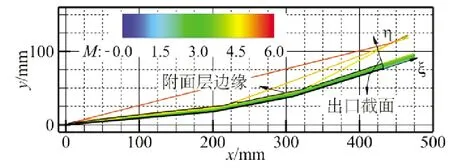
(a)三级斜楔压缩
图6为两个算例出口截面近壁区域的速度和马赫数分布曲线。其中三级斜楔压缩出口截面主流参数均匀,按照0.99倍的定义,附面层厚度应为6.76 mm;而本算法识别的结果为7.04 mm(参见图6(a)),两者相对误差仅4.1%,表明识别的结果是比较准确的。
从图6(b)可见,弯曲压缩型面出口截面主流不均匀,马赫数和速度分布在远离壁面时均有明显增加。按照传统的做法,需要人为选定主流速度的数值,不仅存在较大的主观性,也难以实现自动化的识别。而本算法所识别的附面层边缘位于速度梯度有明显变化的位置,符合附面层的概念。
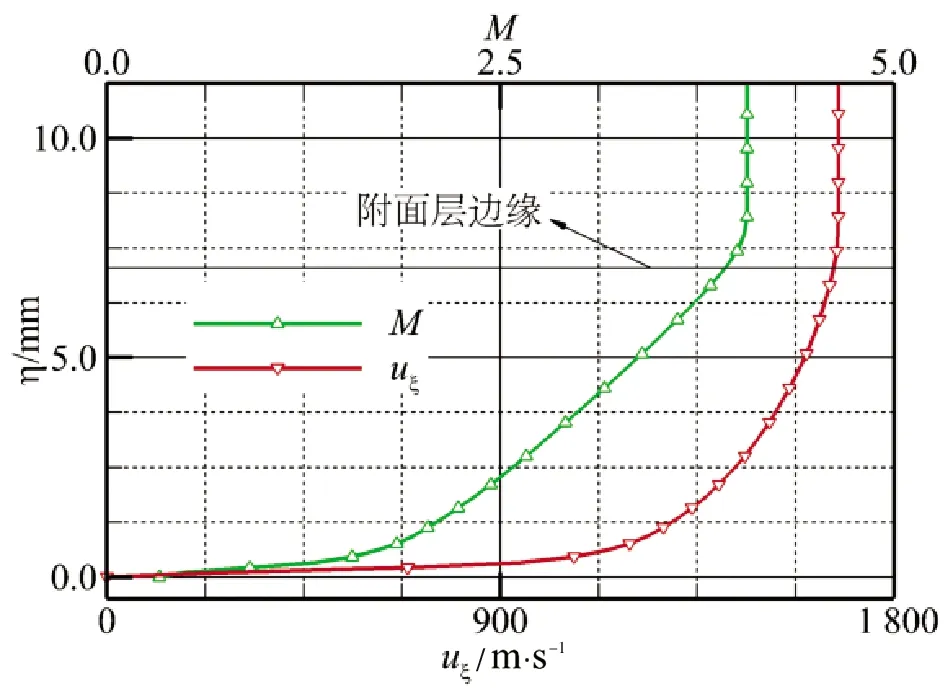
(a)三级斜楔压缩
4 应用附面层修正的型面设计
在工程应用中设计进气道、喷管等流道型面时,常采用先进行无黏设计、再修正附面层影响的方法。在进行修正设计时,通过本文所述的附面层边缘识别方法,能够更准确、方便地获得各截面附面层边缘位置及附面层内参数分布,之后容易根据定义计算其位移厚度δ1:
(5)
其中,δ为附面层厚度,ρ、uξ分别为密度和沿壁面切向的速度分量,下标δ表示附面层边缘位置的参数。对于无黏设计的壁面坐标向外移动该距离可修正附面层对流量的影响。
应用此方法对上述弯曲压缩型面进行了修正。图7为修正前后壁面形状、激波形状的对比,图8为修正前后壁面压力分布及与设计值的对比。可见修正后激波高度与特征线法设计结果的相对误差大约从2.0%降低到0.3%,壁面压力与给定压力分布之间的误差也明显降低,末端压力的相对误差大小|ε|从6.6%降低至2.3%。
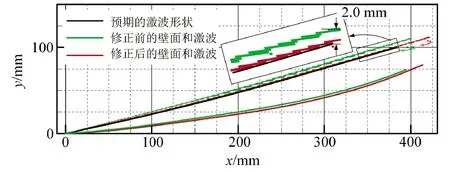
图7 修正前后的壁面形状和激波形状
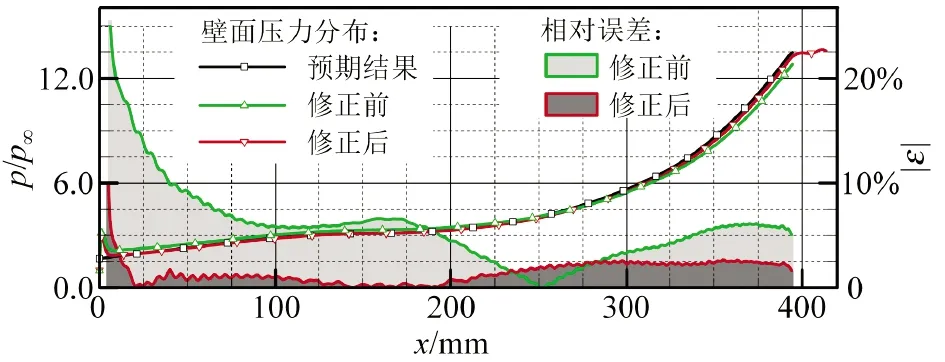
图8 修正前后壁面压力分布及与设计值间的误差
5 结论
1)研究了依据数值模拟结果识别附面层的方法,与依靠经验公式、附面层方程的近似计算相比有更高的精度和更广的适应性;
2)提出了用“参考主流”代替实际主流识别流场附面层边缘的方法:以零剪切力滑移壁面边界条件下数值模拟得到的不受附面层干扰的流场作为参考主流,在根据附面层定义确定其边缘时,以该参考主流流场中的速度代替实际的主流速度进行判断。这种方法避免了传统做法中人为指定主流速度的主观性,因而更为科学合理,也有利于识别过程的自动化;
3)对两个超声速压缩流场附面层识别的测试表明,该识别方法获得的附面层边缘比较准确,其中斜楔压缩出口截面上附面层厚度与采用实际主流速度判断得到的厚度相对误差仅4.1%;
4)根据本算法识别的附面层参数计算位移厚度对弯曲压缩型面进行黏性修正后,激波高度与无黏设计结果之间的相对误差从修正前的2.0%降低至0.3%,壁面末端压力相对误差从6.6%降低至2.3%,表明该方法可取得良好的效果。
