超声压气机叶栅流场的数值模拟与试验验证

唐　凯，葛　宁，顾　杨，向宏辉，马昌友（.中国燃气涡轮研究院，四川江油6700；.南京航空航天大学能源与动力学院，南京006）

超声压气机叶栅流场的数值模拟与试验验证

唐凯1，2，葛宁2，顾杨1，向宏辉1，马昌友1
（1.中国燃气涡轮研究院，四川江油621700；2.南京航空航天大学能源与动力学院，南京210016）

摘要：高超声压气机叶栅因适用于战斗机高马赫数飞行、增压比高而成为研究热点，但其损失难以控制，波系结构复杂，激波附面层干扰结果难以预测。基于自开发NUAA程序，对超声压气机平面叶栅流场进行计算分析，并通过与超声压气机平面叶栅试验结果的对比，考察叶栅在不同进口马赫数与气流攻角下的总性能、波系结构与激波位置。结果表明：程序计算的总性能与试验值吻合很好，且能精确捕捉超声叶栅中的激波结构，较好预测叶片表面等熵马赫数分布，可为超声叶栅的设计与结果验证提供支持。

关键词：航空发动机；超声叶栅；激波；附面层；试验；数值计算

1　引言

航空发动机向高推重比、高效率的方向发展，要求压气机具有级数少、压比高、损失低和稳定工作范围宽等特点［1-2］。从气动设计方面考虑，要达到以上目的，就必须提高压气机的单级加功能力，相应地需要提高转子的切向速度、气流折转角和压气机来流的轴向速度。转子的切向速度主要受到转速、结构尺寸的影响，且受到材料、结构以及激波强度和损失水平等制约。气流折转角的提高受到分离的限制，过大的折转角会导致流动出现严重分离，需要对流动过程精确控制才能提高性能。提高来流轴向速度主要受叶尖相对马赫数的限制，目前一般都控制在1.5以下，以避免激波产生很大的损失。虽然人们采用一些新的叶型设计方法如低展弦比叶片、大小叶片等来进一步提高相对马赫数，但在高叶尖相对马赫数（1.5～2.0）范围内，国内的研究还很少，也少见公开发表文献。

虽然国外以Schreiber为主的学者进行了大量超声平面叶栅（如ARL-SL19、PAV-1.5等叶型）试验，提出了一系列超声叶栅损失模型，包括Balzer［3］、Fottner［4］、Guatafson［5］等激波损失预估方法，但由于不适用于变马赫数工况激波计算，通用性较差。而国内由于受风洞限制，大多学者致力于超声叶栅数值计算，鲜有超声叶栅试验数据支持，不能校核计算结果。基于此，本文应用自开发NUAA程序进行超声叶栅的数值模拟和超声压气机平面叶栅试验，来探索适用于变马赫数工况的超声压气机叶栅仿真计算方法，为超声压气机叶栅的气动设计与结果验证提供理论及数据支持。

2　试验方案

2.1试验设备

试验在中国燃气涡轮研究院超、跨声速平面叶栅风洞上进行。该试验器为暂冲吹入大气式平面叶栅试验器，能进行亚、跨、超声速压气机和涡轮平面叶栅吹风试验，其气流角可调范围为20°～90°，最大流量为22.4 kg/s，稳定工作时间大于4 min［6］。

2.2叶栅试验件

某型超声叶栅（图1），其设计马赫数为1.63，展弦比为1.67，稠度为1.91，通过相似准则对其进行缩放满足平面叶栅二维特性。该试验件由基本叶片、测压叶片和有机玻璃栅板构成，在栅板前缘、对应叶栅通道栅板后缘、测压叶片叶背和叶盆开设壁面静压孔，测取壁面静压。

图1　超声叶栅叶型简图Fig.1 The diagrammatic sketch of the supersonic cascade

2.3试验方法

试验时选取对应喷管，并通过调压阀调节进口马赫数。由于是超声叶栅，进口壁面附面层较厚，在试验段前端对附面层进行抽吸，并根据栅前壁面静压孔压力分布调节各段抽吸压力。试验时，通过转动圆盘调节气流攻角，栅后通过三孔楔形探针测量参数，并运用尾迹处理方法处理栅后出口平面采集数据。分别对设计马赫数下的攻角特性和设计攻角下的速度特性进行试验。

2.4测试方法

叶栅风洞测试系统主要由VXI数据采集系统、PSI数据采集系统、位移机构系统、纹影仪系统、与后端数据处理系统构成，各系统之间通过TCP/IP协议进行数据通讯。利用VXI系统采集气体压差、温度等；利用PSI系统采集稳压段总压，栅前、栅后壁面静压及栅后三孔探针压力；纹影系统主要用于测量激波位置。通过油流照片补充叶片表面激波位置和附面层分离及再附位置。

3　NUAA程序

由于商业软件集成性高，对于研究工作的某些特殊问题，用户无法改变其集成的计算方法和参数设置，加之现阶段激波损失模型不完善，激波产生出现流场强间断造成的数值计算精度低、易发散等问题，极大地限制了商业软件的使用。本文采用自开发NUAA程序，能添加新型数值解法，并能根据试验结果修正模型。

NUAA计算程序以计算流体力学的基本N-S方程为基础，给出了不考虑体积力和外部热源的原始N-S方程。然后对方程进行无量纲化及笛卡尔坐标系到一般曲线坐标系的坐标转化，给出一方程S-A湍流模型的控制方程。最后将N-S方程组和湍流模型方程进行联立，写成统一的守恒形式。

计算共考虑六个方程，即一个连续方程、三个动量守恒方程、一个能量守恒方程、一个S-A湍流模型方程。求解过程中，将前五个方程进行耦合求解，S-A湍流模型方程单独求解，每步迭代结束后更新六个方程中的守恒变量数值。采用具有高间断分辨率的Roe通量差分裂方法［7］进行无粘对流通量的空间离散，使用三阶MUSCL插值方法计算插值过程中左右两侧原始变量，加入TVD格式的一种修正［8］以防激波附近流场参数变化剧烈而引起计算震荡。修正形式为：

公式右边第一项为一阶精度的对流通量，第二、第三项是对一阶通量的修正，最后得到公式左边高阶精度的对流通量，并对修正项加入Van Leer限制器。扩散通量采用二阶中心差分格式离散。从数学本质上看，对流通量属于双曲型，扩散通量属于抛物型。因此，对方程组进行时间推进时，对流通量采用隐式处理，加速收敛；扩散通量采用显式处理。

4　网格生成与边界条件

通过NUAA程序网格前处理程序，生成平面叶栅H-O-H网格（图2），网格数共44 932。计算过程中，给定进口总压、进口总温、进口等熵马赫数、进口速度方向和出口背压，叶片表面采用无滑移边界条件，流道侧面采用周期性边界条件，物性条件按理想空气计算。图3为网格生成流程图，图4为流场计算原理图。

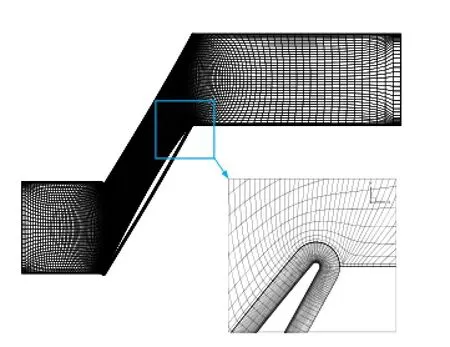
图2　流场计算网格Fig.2 Flowfield grid map

图3　网格生成流程图Fig.3 The grid generating flow chat

5　计算结果与试验结果对比

叶栅的总性能是决定叶栅计算结果好坏的一大依据，表1给出了数值模拟与试验结果对比。表中，Ma1为叶栅进口马赫数，Ma2为叶栅出口马赫数，i为进口气流攻角，σ为总压恢复系数。可见，试验值与计算值的总性能差别很小，且随进口马赫数的增大，其总压恢复系数误差呈减小趋势。最大误差4.6%出现在Ma1=1.63、i=1.42°处，说明该程序对于叶栅总性能的计算有较高的精度。此外，随着进口马赫数的增大，总压恢复系数不断减小，说明因激波及激波附面层干扰造成的损失不断增大。

图4　流场计算原理图Fig.4 The calculating principle of flowfield

表1　数值模拟与试验结果对比Table 1 The comparison of the CFD and test results

从图5中计算结果与图6中纹影图片的对比可以看出，此叶型的激波结构有脱体弓形激波、前通道激波、尾缘激波和前通道激波反射波四种，计算结果与试验结果吻合很好。随着进口马赫数的升高，前通道激波入射位置后移且激波强度增强，导致叶片吸力面附面层增厚甚至分离，从而在叶背处产生λ激波；反射激波强度也随之增强，从而在叶盆处也诱导产生了λ激波（图5（c）。另外，进口马赫数升高使得叶盆、叶背表面等熵马赫数差异增大，说明高马赫数下叶栅前缘头部和弓形波对叶盆、叶背的影响变大。随着进口气流攻角的减小，尾缘激波前移，叶背附面层分离现象逐渐消失。

图5　不同进口条件下的叶栅流场等熵马赫数分布云图Fig.5 Mach number distribution of the cascade flowfield at different working condition

图6　不同进口条件下的叶栅纹影图Fig.6 The cascade schlieren at different working condition

对于超声压气机叶栅，波系结构决定其增压能力，这也是CFD计算的难点。尤其是存在激波时，由于激波附面层干扰的复杂性，叶片表面等熵马赫数分布计算结果很难与试验结果一致。并且，由于在高超声压气机叶栅试验中，气流通过叶栅时存在很高的逆压梯度，使得试验段两侧端壁附面层发展，虽然采用抽吸装置及尾板调节能一定程度削弱侧壁附面层发展，但仍会影响轴向速度密度比（从图7中油流照片可以看出，两侧端壁附面层的影响区域在叶盆处达50%叶高）而改变叶片表面等熵马赫数分布。从图7中可以看出，附面层在叶背70%弦长处发生分离，而叶盆在65%弦长处发生分离，此结果与图5（b）中前通道激波、尾缘激波入射位置相近。从图8中可知，Ma1=1.30、i=0°时，叶片表面等熵马赫数分布计算结果与试验结果一致性很高，只是尾缘激波在叶盆处的入射点有所差异。结合等熵马赫数分布云图图5（a）可知，气流在叶背加速区达50%弦长，后经前通道激波减速增压，此处激波发展成λ激波，激波入射点前附面层增厚，产生压缩波区域汇聚为一道反射激波，组成λ激波的前支。因为激波只出现在超声区，粘性层内不存在λ激波后支，所以图8中没有观察到λ激波后支，但在云图中可见λ激波后支的存在。激波后流道呈扩张状，气流继续加速，在80%弦长处，由于尾缘激波的产生气流降速增压。在叶盆30%弦长处气流由于前通道激波反射波的存在而减速，后又经尾缘激波达到增压目的。但是由于整个流场内都是超声气流，据此可判断通道内并不存在正激波增压，所以其增压效果较差。

图7　Ma1=1.63、i=0°时叶片表面的油流照片Fig.7 The oil flow of blade surface atMa1=1.63，i=0°

图8　叶片表面等熵马赫数分布对比Fig.8 The comparison of Mach number distribution of blade surface

6　结论

对超声叶栅进行试验研究，并利用自开发NUAA程序对各工况下流场进行数值模拟，通过试验结果与计算结果的对比可得到以下结论：

（1）程序计算结果与试验结果总体上吻合很好，计算所得波系与试验结果相符，只是尾缘激波位置和强度与试验结果有所差异。这是由于前通道激波与附面层强烈干扰引起流场复杂的原因。

（2）利用等熵马赫数分布云图可以解释试验过程中叶片表面马赫数变化原因，并弥补纹影图片采

集中反射激波与λ激波成像较差的缺陷；并且通过程序得到的叶片表面等熵马赫数图，能很好地解释纹影图片中出现的激波系，为试验中离散的叶片表面等熵马赫数点作补充。

（3）随着进口马赫数的增大，前通道激波入射点后移并引起吸力面附面层分离，而由前通道激波引起的反射波则诱导叶片压力面产生大范围低速区；随着攻角的增大，叶片压力面甚至也出现了λ激波，产生了经典的激波诱导附面层分离现象。

（4）通过NUAA程序，能较为准确地得到超声叶栅总性能和叶栅内部流场分布，可为超声叶栅的设计与试验研究提供支持。

参考文献：

［1］ 刘大响，程荣辉.世界航空动力技术的现状及发展动向［J］. 北京航空航天大学学报，2002，28 （5）：490—496.

［2］ 陈海生，谭春青.叶轮机械内部流动研究进展［J］.机械工程学报，2007，43（2）：1—12.

［3］ Koch C C，Smith Jr L H.Loss sources and magnitudes in axial flow compressors［J］.ASME Journal of Engineering for Power，1976，98：411—424.

［4］ Fottner L.Survey of models for shock and shock/boundary layer interaction loss prediction［C］//.Hirsch C，Denton J D.Through flow calculations in axial turbomachines. AGARD-AR-175，1981.

［5］ Gustafson B A.A simple method for supersonic compressorcascadingperformanceprediction［R］.ASME 76-GT-64，1976.

［6］ 姜正礼.流场显示在超、跨声速平面叶栅试验中的应用［J］.燃气涡轮试验与研究，1998，11（1）：1—5.

［7］ Roe P L.Approximate Riemann solvers，parameter vectors，and difference schemes［J］.Journal of Computational Physics，1981，43：357—372.

［8］ Janus J M.Advanced 3-D CFD algorithm for turbomachinery［D］.Mississippi：Mississippi State University，1989.

中图分类号：V231.3

文献标识码：A

文章编号：1672-2620（2015）03-0008-05

收稿日期：2014-08-20；修回日期：2015-06-17

作者简介：唐凯（1988-），男，四川江油人，硕士，主要从事压气机及叶栅试验技术研究。

Numerical simulation and experimental investigation on supersonic compressor cascade flowfield

TANG Kai1，2，GE Ning2，GU Yang1，XIANG Hong-hui1，MA Chang-you1
（1.China Gas Turbine Establishment，Jiangyou 621700，China；2.College of Energy and Power Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Abstract：Supersonic compressor cascade has become a key issue for its high pressure ratio and applying to high speed fighter.But its loss is uncontrolled，the shock wave system is complex and the shock wave and boundary layer interaction are unpredicted.Based on NUAA program for supersonic compressor cascade flowfield，calculation analysis was conducted.And through the comparison between calculation results and experimental investigation，the performance parameters，shock formation and shock location at the condition of different Mach number and attack angle were discussed.The results show that the NUAA program could correctly predict the shock wave structure and surface Mach number distribution，and the simulation results were good agreement with the experimental results.The program is helpful for supersonic compressor cascade design and testing result validation.

Key words：aero-engine；supersonic cascade；shock wave；boundary layer；experiment；numerical simulation