构建深度学习课堂,促进数学核心素养的养成
2020-09-12马志洲
马志洲

[摘 要] 文章基于深度学习理论,以“反比例函数等积模型”的教学为例,探讨基于数学核心素养的深度学习课堂构建策略,认为教学中教师应更加关注学生“想”的过程,使他们在深度学习中实现数学素养的生长.
[关键词] 初中数学;深度学习;核心素养;反比例函数;等积模型
深度学习的目的是将处于理解、了解、记忆层面的知识与技能转化为分析、应用、评价以及创造等更高层次,也就是由传统的注重学生学习成绩的高低转化到“思维思辨”等数学核心素养的培养上来[1] . 而初中阶段的学生身心发展尚未完全成熟,对于相关知识的学习往往停留在浅层次上,如果在具体教学中缺乏深度学习,则会严重影响学生学习思维能力的发展,也无法达到举一反三、触类旁通的学习效果. 因此,思考如何激发学生的深度学习,探究如何构建深度学习课堂教学策略具有重要的意义.
基于数学核心素养的深度学习
课堂构建策略
1. 设定教学目标,创设问题情境,引导学生归纳总结
并不是所有的教学内容都要求学生同等程度地掌握,因此,教师应结合课程标准的规定,明确划分需深层掌握和浅层了解的知识内容,科学设定教学目标. 同时,教师还应充分鼓励学生利用自己已有知识和学习经验,主动获取和构建新知识. 实质上,深度学习课堂的构建,不仅要求学生理解概念、原理等结构化的浅层知识,还要求学生将这些概念、原理等形成体系,并应用到实际问题的解决中去. 所以教师还应尽可能地创设情境,引导学生将所学知识与课堂情境联系起来,并要求学生根据学习内容以及教学目标,自己去总结和归纳所学知识,有效促进相关知识的正向迁移.
2. 设计问题链,注重学生思维暴露,引导学生提出问题
良好的问题链设计是培养学生思维方式、促使学生理解所学知识的有效手段,因此,教师应选择一些灵活的或有层次性的问题,最大限度地激发学生探究和思考的热情. 例如,在组织学生学习“反比例函数等积模型”时,笔者不仅设计了能引出解决几何问题新方法的基础性问题链,还设计了旨在让学生进一步理解几何含义的逆向思维问题链,最后,根据学生的学习情况,设计了旨在巩固和概括问题解决方式的综合性问题链. 除此之外,在具体教学过程中,教师还应诱导和启发学生的思维,适时提供暴露学生思维活动的机会,准确掌握学生真实的思维情况,并充分展示其思考过程和具体解法. 也要引导学生将知识构建中的困惑大胆地表述出来,从而让学生真正参与到解题的思维过程中,有效促进学生深层次思维的发生.
3. 熟练掌握教材内容,注重变式引导,让学生触及知识本质
由于课堂空间和时间的有限性,在教学前,教师应深度理解教材的内容,并根据学情不断整合教学内容,适当对所要学习的知识进行压缩和精选,有效把丰富的、繁杂的数学知识精简成简单的命题. 也就是说深度教学应触及数学知识的本质,要通过各类变式不断引导学生深入探寻知识的来源和背后所蕴含的思想方法,将学生认为最有价值和最需要的知识呈现在学生面前,促进学生不断走向思维深处[2] . 例如,在“反比例函数等积模型”题目中,为了突出k的几何意义,在相关辨析中总结k的本质意义,笔者设计了k矩形和k三角形两种模型,同时,在问题解决过程中采用一题多解和一题多变等形式.
4. 注重自我反省,不断内化知识,实现知识迁移
“授之以渔”比“授之以鱼”更重要,因此,教师不仅要给学生传授相关的知识与技能,更为重要的是要引导学生学会反思,促使学生自主发现问题、解决问题,主动建立知识与知识之间的联系,最大限度地引导学生真正成为学习的主人. 例如,笔者在组织学生学习“反比例函数等积模型”内容后,及时引导学生进行自我评估,并通过图示的形式要求学生将所学内容呈现出来,从而更好地把握自身深度学习的情况. 同时,还应引导学生不断理解所学知识,对所学内容做出批判性吸收,并鼓励学生对所学内容进行深层次的思考和亲身体验,不断改正学习中存在的问题,实现学习迁移. 例如,在组织学生探究“反比例函数等积模型”时,为了充分调动学生探究的積极性,让不同学生的思维火花进行有效碰触,笔者设计了“类比上述做法,试着在第一象限内设计出反比例函数y= 与坐标轴所形成的阴影部分面积为6的四边形”等开放性题目.
基于数学核心素养的深度学习
教学实践
教学仅有相关理论是不够的,而基于数学核心素养的深度学习课堂构建理应是理论联系实际的. 作为初中三大函数之一的反比例函数,其有关面积的模型一直是各类考试所关注的焦点,并且,反比例函数的多种性质还可以和其他函数进行结合,相当数量的学生遇到反比例函数中的面积模型题目时往往望而兴叹. 因此,为了让学生在教学中实现深度学习,笔者以“反比例函数等积模型”为例进行深入探究.
1. 观察图像,解释内容本质
为了有效复习反比例函数相关的知识,促使学生正确理解反比例函数y= (k≠0)中k的几何含义,笔者设计了如下题目:
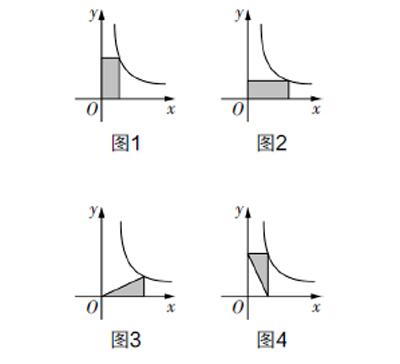
如图1~图4所示,试求反比例函数y= 与坐标轴所形成的阴影部分的面积.
如图5~图8所示,试求反比例函数y= 与坐标轴所形成的阴影部分的面积.
2. 逆向思维,增强学生的创新意识
为了充分激发学生的创造力,多角度、多层次地探索数学问题,笔者要求学生通过观察、分析、对比、猜想、推理等一系列探究活动,探究如下开放性问题:
(1)已知反比例函数y= ,类比上述做法,试着设计出反比例函数y= 与坐标轴所形成的阴影部分面积为6的四边形.
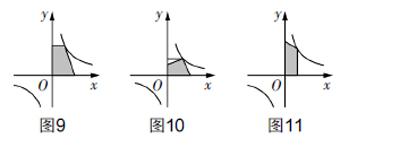
在此过程中,教师应及时给予帮助和指导,并引导学生呈现出如下典型做法,如图9~图11.
(2)能否借助反比例函数y= 和反比例函数y= 图像上各一点,设计出阴影面积为2的四边形?
在此过程中,教师及时地给予帮助和指导,并引导学生呈现出如下典型做法,如图12~图14.
3. 善用变式,形成活动经验系统
为了进一步巩固所学知识,突出k的几何含义等重要内容,帮助学生形成活动经验系统,笔者根据学情设计了如下变式练习题目.
(1)如图15所示,已知点P在x轴上,点A在反比例函数y= 上,AB⊥y轴,且△APB的面积等于5,试求k的值.
(2)如图16所示,已知正比例函数y=kx与反比例函数y= 相较于A,B两点,试求以下问题:
①若AC⊥x轴,则试求△OAC的面积.
②连接BC,则试求△ABC的面积.
③过点B作BD⊥AC交AC的延长线与D,则试求矩形AEBD、△ABD的面积.
④如图17所示,已知反比例函数y= (其中k>0,x>0)与矩形OABC相交与E,F两点,并且EB=EC,试求F为AB的中点.
综上所述,为了达到深度学习的目的,教师应更加关注学生“想”的过程,并通过创设教学情境、分类设定教学目标、科学设计问题链、设置开放性问题,以及变式练习、归纳总结等方式,不断引导学生“如何想”“想什么”,多角度、多层次、有序地促使学生感悟解决问题的本质,从而实现从理解、到整合、再到分析与创造的真正深度学习的目的.
参考文献:
[1]马晓琴. 初中数学深度学习的基本理解与实施策略[J]. 数学教学通讯,2018(8).
[2]王道宇. 初中数学深度学习的实践研究[J]. 中学数学教学,2019(10).
