对一些课堂导入情境的探析
2020-09-12万志建

[摘 要] 好的教学情境能最大限度地激发学生学习的积极性,其重要性不言而喻. 文章以四个教师评优课的课堂导入情境为例,分析存在的问题,探析解决之道,指出课堂导入情境要注重过程体验,内容整合,重点突出,形成主线.
[关键词] 情境;体验;整合;重点;主线
近期接连听了四个区的青年教师评优课,这些教师来自各区不同的学校,平均年龄在35周岁以下,课堂上他们展示了各具特色的教学风采,取得了较好的教学效果. 笔者在欣赏学习之余也感觉有些美中不足,很多教师的课堂导入情境不尽人意,由此引发笔者对课堂导入情境的思考,下文结合教师在教学过程中展示的情境,谈一些看法和设想.
过程跳跃,缺少体验
案例1 人教版“平方根”课堂引入.
情境再现:
A教师:先出示表格,已知正方形面积是整数和分数的平方数,求边长. 然后追问学生,如果正方形的面积是2,边长是多少?学生一时语塞,接着A教师说,面积等于2的正方形的边长我们很难直接表示,今天我们就来解决这个问题,从而引出平方根的概念……
B教师:先让学生把4个全等的腰长为1的等腰直角三角形纸片拼成一个正方形,并求这个正方形的面积,然后问学生该正方形的边长是多少?学生一时有些茫然,接着B教师操作同上.
问题透视:
对于A教师的引入,笔者不禁反思,突然来一个“平方等于2的数,求这个数?”学生会不会纳闷,究竟有没有平方等于2的数?
对于B教师,引入设计相对自然,但在课堂小结时,一位女生站起来问,老师,我想知道 是一个什么样的数,有多大?老师说, =1.414……那位女生似懂非懂地坐下了,但从她犹豫的神态中可以看出她还不是很明白.
我们引入平方根,主要是为了表示一些开平方开不尽的数与式,但在表示之前,首先要让学生明白这样的数是否真实存在. 毕达哥拉斯学派在这之前也一直持否定态度,甚至视其为异端邪说,更不要说仅凭老师三言两语就能让学生领会认可. 其次要让学生接受这个数,首先要让学生看得见、摸得着,从具体到抽象拾级而上,否则拼正方形也就成了形式.
情境重置:
(1)出示问题:已知等腰直角三角形ABC的腰长为1 cm,如何求它的面积,有哪些方法?
有两种方法:一种是面积等于两腰乘积的一半即为 ;另一种把斜边看作底,它的面积等于 斜边长乘以斜边上的高,但不知道斜边和斜边上的高分别是多少.
(2)如果作出等腰直角三角形ABC斜边上的高,有什么发现?设斜边长为x cm,试用x表示高,由此可发现什么等量关系?
发现分成两个形状大小一样的等腰三角形,此时高为斜边的一半,即为 x cm,S△ABC= x2= ,由此可得x2=2.
(3)这样的x存在吗,就是那条边长?量量试试看,值是多少?是有限小数吗?会是分数吗?
发现x在1.4 cm左右,1.5 cm不到,是一个无限不循环小数.
(4)類似这样的无限不循环小数以前在哪里出现过,当时如何处理的?猜想我们现在会怎么办?
小学里碰到圆周率,引进希腊字母π表示,猜想我们会引进新的表达方式.
信息分散,缺少整合
案例2 苏科版“5.1 二次函数” 课堂引入.
情境再现:
四位教师在上该课时,其中两位教师直接引用书上三个例子,水滴激起的波纹形成的圆的面积与半径的关系、周长为16 m的长方形生物园面积与长的关系及加工矩形镜子的费用与镜面宽的关系,得到三个函数关系式,通过归纳共性得到二次函数概念;另两位教师以“面积、费用、利润、增长率”等为背景设计了若干问题,得到一些一次函数和二次函数,然后让学生分类比较,引出二次函数概念.
问题透视:
无论是教材提供的例题还是教师自己设计的例题,尽管知识面宽泛,但只是围绕二次函数这一主题呈现各类题型组合,相互之间的关联性不强,过渡也不够自然紧密,缺少一条主线,导致学生的思维应接不暇,不断处于间断调整状态,思维的连续性、发散性、深刻性不够. 概念课情境的设计,应尽可能围绕某一情节把一些典型的事例有机串联起来,呈现生活、简约、发散、高效的意境,产生“少而精”“单而丰”的教学效果,让概念的提炼经历从模糊到清晰,从具体到抽象,从发散到聚集,层层推进,回归本质的过程.
情境重置:
(1)出示问题:回顾学习一次函数及反比例函数概念的经历.
发现都是通过生活中的具体例子,抽象出相应的关系式,通过辨析比较,得出相应的概念.
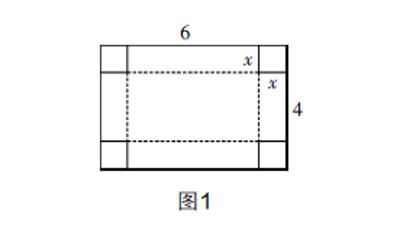
(2)对于二次函数的学习,我们也不例外,出示例题:如图1,现有边长为x(厘米)的小正方形在矩形的四个角,把图形围成一个无盖的长方体纸盒,请设计一个跟面积(用y表示)有关的自变量为x的函数表达式.[1]
得出以下函数表达式:y=x2,y=4x2, y=-4x2+24 ,y=-8x2+20x,y=4x2-20x+24.
(3)这些函数有什么共同特征?给它们起个名字,结合其中“相貌”最威武的那个函数的“长相”,描述二次函数的定义,并说说你的理解.
发现未知数的最高次数为二次,最后一个函数最威武,联想到一元二次方程的一般式,可把形如y=ax2+bx+c(a≠0)的函数叫作二次函数,其中x是自变量,y是x的函数……
课题解读,重点偏失
案例3 苏科版“从问题到方程” 课堂引入.
情境再现:
七位教师在上该课时,四位教师直接开门见山介绍篮球赛引出方程,然后通过例题和习题反复训练如何寻找等量关系列方程,书上天平平衡的例子只是作为寻找等量关系的一个练习或随口提了下;一位教师干脆不用书上的例子,直接以“猜年龄”或“月历中的数字和的组合”引出方程再举例如何列方程;还有两位教师先讲天平的例子得出方程,但没有点明天平平衡与方程的关联,然后直接出示篮球赛的例子让学生找等量关系列方程.
问题透视:
上述几位教师的引入情境让人感觉有些意犹未尽,对“从问题到方程”的核心词“到”的解读不够尽兴. “到”字应彰显二层含义,一是为什么要到,要体现价值导向,同样一个问题,让学生体验用小学熟悉的算术方法与小学初学的方程解答,比较孰优孰劣,从而逐步克服习惯用算术方法解应用题的思维定式,体会到用方程解应用题的优越性源于思维的正向性,用字母表示数的简洁性;二是怎么到,要体现模型支撑,借助天平,让学生通过动手操作,体验方程是表示数量之间相等关系的“天平”,同时为后面学习“等式性质一”奠定基础,也为学习不等式暗埋伏笔.
鉴此,笔者认为,教师一开始,不管创设什么情境,首先可设计一个让学生通过算术或方程都可以上手的问题,接着增加些难度,变成用算术方法解决有难度,而用方程解决相对轻松的问题,让学生在比较中感受方程的优越性,然后借助天平,让学生感受生活中平衡的例子,体验方程模型.
情境重置:
(1)出示问题:据悉,我班同学年龄最小是14岁,正好是老师年龄的 还少1岁,请问老师年龄是多少?多少年后,老师的年龄是这位同学的2倍?
学生体验用算术和方程两种方法分别求解.
(2)两种方法有何不同?哪种方法更简捷,为什么?
无论哪一种方法,本质上都是利用等量关系来解决:一种逆向思维,用语言文字来揭示其中的等量关系,根据文字的逻辑关系,由外而内步步倒推,直接求出年龄;另一种正向思维,设未知数,用字母表示等量关系得到方程,借助等式性质,由外而内抽丝剥茧,求出未知数的值. 后者更显简捷易懂,一是正向思维自然顺畅,二是用字母表示年龄简明扼要,三是解答过程比较轻松.
(3)究竟怎样寻找题中隐含的方程呢,关键是什么?我们来体验一下天平称重,从中找找启发……
学生上台操作,体验天平平衡时左右托盘中物品质量相等的关系,如果把质量抽象成代数式,即意味着两边代数式相等,从而领会方程是表示数量之间相等关系的“天平”.
内容繁杂,缺少主线
案例4 苏科版“角”课堂引入.
情境再现:
七位入职不到三年的新教师上评优课“角”,其中有一位新教师是先从球员射门角度的大小引入新课,另外三位新教师从具体图形出发,抽象出角的形状,再介绍角的定义、命名、角的单位、角的大小比较以及角的组合,还有三位新教师是从回顾“线段”的学习过程说起,并板书线段的学习过程,在接下来的讲解中按照学习“线段”的过程,一步一参照,介绍“角”的内容.
问题透视:
从听课情况来看,前四位教师对知识点的分析讲解比较到位,但由于整堂课知识点比较多,因而内容的介绍略显忙乱,教师疲于介绍,学生被动接受,个别教师甚至有些顧此失彼. 后三位教师在展示过程中,由于有了“线段”学习过程的参照,介绍时相对轻松许多,但还不是放得很开,一步一参照,缺少一气呵成的宏观与大气. 章建跃博士说过:“代数要教归纳,几何要教类比. ”纵观初中几何内容的学习,有很多共性通法,例如在概念的定义上一般都以低维图形定义高维图形;在知识的呈现上一般都以“概念、符号表示、性质、判定”这样的主线展开,所以教师在授课时要有意识地把这些方法思路渗透其中,让学生潜移默化,掌握几何学习的一般规律.
解读教材时不难发现,“角”的知识呈现跟“线段”非常类似,因此在介绍“角”的内容前,可让学生先回顾“线段”的学习内容,不仅要罗列出知识要点,串联形成知识线,还要回顾数学思想方法,让知识线与思想方法线交汇融合,比翼双飞. 再通过类比转化,一以贯之,直接让学生得出“角”要学习的内容,在未学之前便可初知整体框架,这样既有方向,也有方法,学习也就更显得自觉主动,活泼生动.
情境重置:
(1)出示问题:同学们,上一课我们学习了“线段”,先后讲了哪些内容?请按序罗列这些内容以及涉及的一些思想方法.
回顾得出如下内容:
知识线:概念——表示——度量——长短比较——组合.
思想线:
(2)提出问题:几何内容很多是相似相通、螺旋上升的,今天我们学习“角”这一内容,跟“线段”这一内容非常类似,请你们模仿“线段”的学习谈谈“角”要学习的内容.
“角”学习的内容:概念——表示方法——度量单位——大小比较——组合.
写在最后
课堂导入情境,一是要以体现数学内容本质为根基,二是要以促进学生思考和交流为目的,三是要以思想方法引领为导向,因此情境设计要考虑以下三个方面:一是要体现知识性,情境设计必须要指向本课研究的核心问题;二是体现吸引性,无论设计生活情境还是知识结构情境,都要让学生感兴趣,能吸引学生自觉主动地参与其中;三是体现方法性,情境的设计要体现数学知识的学习规律和方法,潜移默化,让学生学会学习. 在情境的呈现上一要重视探究的过程,让学生身临其境,融入其中,品味知识的形成发展过程;二是要让情境创设的初始问题及由此引出的后续问题形成教学的主线,贯穿于课堂教学的始终 [2];三是要体现一定的思维深度,渗透各种数学思想方法,让数学思想方法伴随情境的发生发展.
参考文献:
[1]万志建. 从“开篇、连线、勾廓”的视角谈章首课设计——以苏教版“5.1 二次函数”为例[J]. 中学数学,2019(22).
[2]浦叙德. 课堂引入情境:既要选好 ,更要用好——以苏科版八(上)“6.3 一次函数的图像(1)”为例[J]. 中学数学,2016(4).
