对一道高考试题的再探究

福建省福鼎市第六中学(355200) 谢卿孝

《数学通讯》2019年第11 期(上半月)有三篇文章谈及2019年全国卷Ⅱ理科第21 题,给出了试题的多种解法及试题的源与流,其中文[2]和[3]还分别给出了试题的推广,其中对该试题的第(2)(i)小题给出了类似的推广结论.读后颇受启发,但觉意犹未尽,还可以继续进行探究,得到新的结论.先把原试题及文[2]和[3]对试题第(2)(i)小题的推广结论抄录如下:

试题(2019年高考全国卷Ⅱ理科第21 题)已知点A(−2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率之积为记M的轨迹为曲线C.

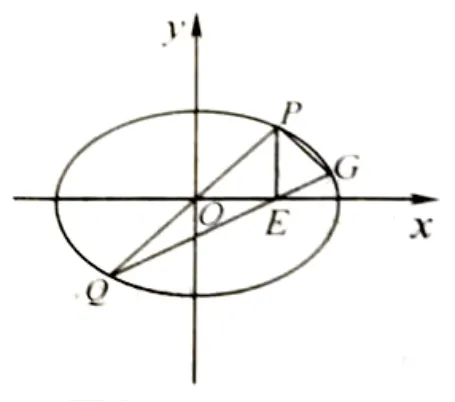
图1

(1)求C的方程,并说明C是什么曲线;

(2)过坐标原点的直线交C于点P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连接QE并延长交C于点G.(i)证明:∆PQG是直角三角形;(ⅱ)略.

性质A(文[2]的结论3 与文[3]的结论(1)的综合)已知椭圆过坐标原点的直线交椭圆C于A,B两点(A,B与椭圆C的顶点不重合),AM⊥x轴于点M,直线BM交椭圆C于点D,直线AB,AD的斜率分别为k1,k2,则有

探究1在性质A 中,有两个条件(1)(2),一个结论(3):

若设A(x0,y0),则由条件(1),(2)可以得到B(−x0,−y0),M(x0,0),及

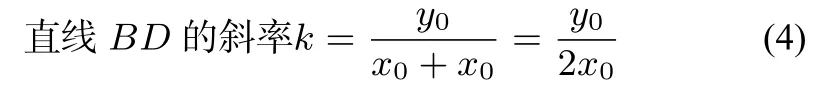
如果去掉条件(2),(4)也可以由(1)(3)得出.

结论1已知椭圆过坐标原点的直线交椭圆C于A(x0,y0),B两点(A,B与椭圆C的顶点不重合),点M在x轴上,直线BM交椭圆C于点D,AB,AD的斜率分别为k1,k2,则的充要条件是BD的斜率

探究2如果k1k2=λ(λ为非零常数),那么,其充要条件是什么? 经探究,可得

结论2已知椭圆过坐标原点的直线交椭圆C于A(x0,y0),B两点(A,B与椭圆C的顶点不重合),点M在x轴上,直线BM交椭圆C于点D,AB,AD的斜率分别为k1,k2,λ为非零常数,则k1k2=λ的充要条件是直线BD的斜率

证明由点A(x0,y0)及直线AB过坐标原点,得B(−x0,−y0),且由探究1 知若k1k2=λ,则

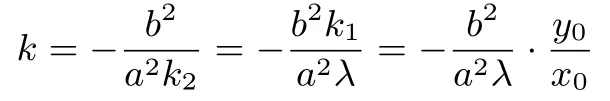
在结论2 中,若设M(xM,0),则

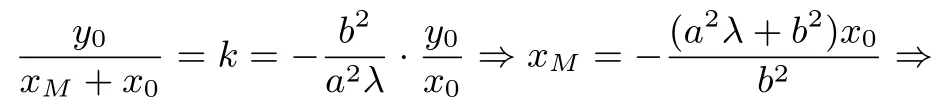
直线AM的斜率由此可得结论2 的

推论已知椭圆过坐标原点的直线交椭圆C于A(x0,y0),B两点(A,B与椭圆C的顶点不重合),点M在x轴上,直线BM交椭圆C于点D,AB,AD的斜率分别为k1,k2,若k1k2=λ(λ为非零常数),则直线BD,AM的斜率分别为

特别地,当a2=4,b2=1,λ=−1 时,

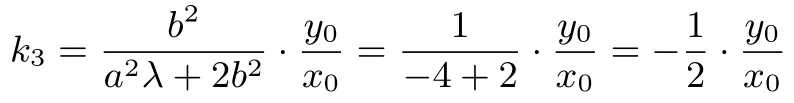
这就是2014年全国高考山东卷文科试题题21 第(2)(i)小题的结论:在平面直角坐标系xOy中,椭圆的离心率直 线y=x被椭圆C截取的线段长.(1)求椭圆C的方程(答案:椭圆C的方程为;(2)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴,y轴分别交于M,N两点.(i)设直线BD,AM的斜率分别为k1,k2,证明存在常数u,使得k1=uk2,并求出u的值;(ⅱ)略.

探究3上述结论2 保留了结论1 中的条件(1),去掉条件(2),如果保留结论1 中的条件(2),去掉条件(1),会有什么相应的结论? 即若AM⊥x轴,则直线AB,AD的斜率k1,k2之积k1k2=λ的充要条件是什么? 经探究,可得

结论3已知椭圆=1(a＞b＞0),A(x0,y0),B在椭圆C上(A,B与椭圆C的顶点不重合),点M在x轴上,直线BM交椭圆C于点D,AB,AD的斜率分别为k1,k2,λ为非零常数,且AM⊥x轴,则k1k2=λ的充要条件是直线BD的斜率

证明由A(x0,y0),AM⊥x轴可得M(x0,0).设直线BD的方程为y=k(x−x0),代入椭圆方程,得b2x2+a2k2(x−x0)2−a2b2=0,整理得

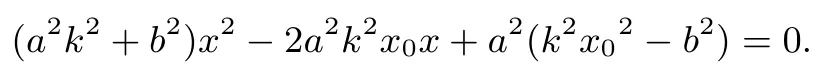
设B(x1,y1),D(x2,y2),据韦达定理,得

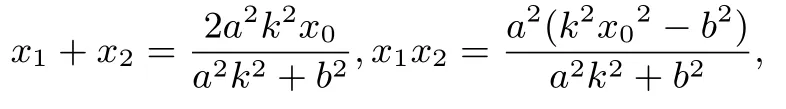
则

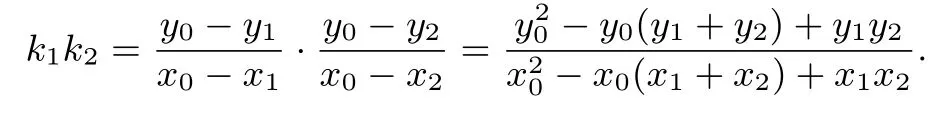
又

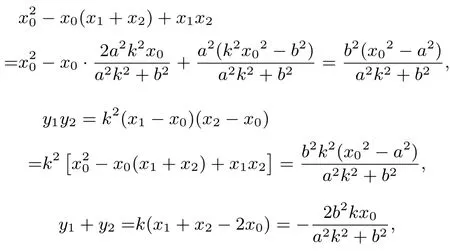
则

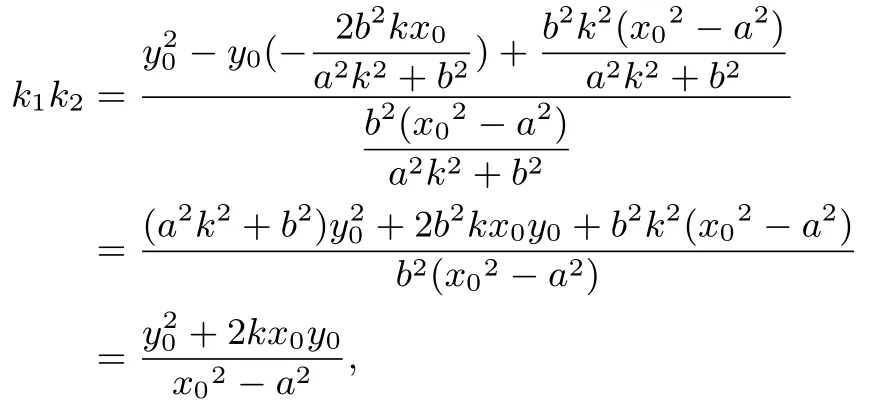
于是

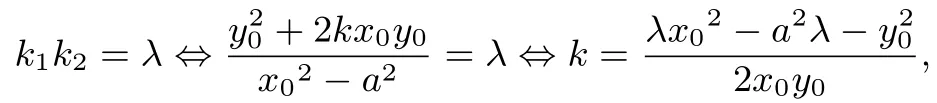
即

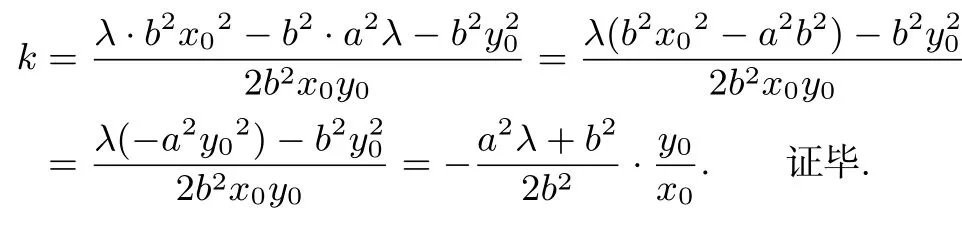
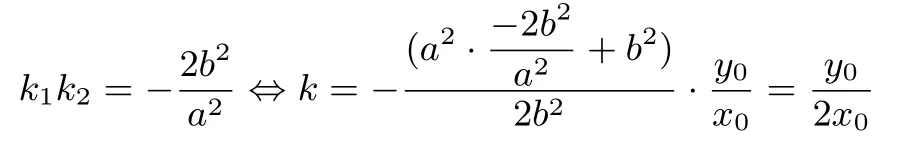
结论3 即结论1.

探究4上述结论2、3 分别保留了结论1 中的一个条件,去掉另一个条件,如果把两个条件同时去掉,会有什么相应的结论? 即设点A(x0,y0),B,D均在椭圆上,则直线AB,AD的斜率k1,k2之积k1k2=λ(λ为非零常数)的充要条件是什么?经探究,可得

结论4已知椭圆点A(x0,y0),B,D均在椭圆C上,直线AB,AD的斜率分别为k1,k2,λ为非零常数,则(1)当时,k1k2=λ的充要条件是直线BD的斜率当时,k1k2=λ的充要条件是直线BD过点

特别地,当a2=4,b2=2,直线BD过点时,据结论4(2)的充分性,得

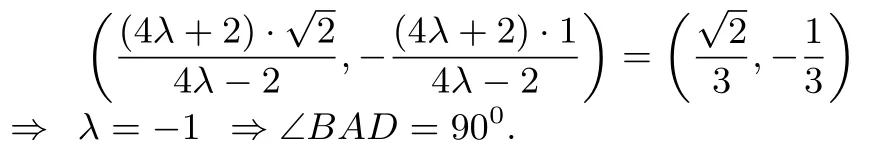
这就是2011年全国高中数学联赛湖北预赛第11 题第(1)小题的答案.该题目为:已知椭圆过点而不过点的直线l交椭圆C于A,B两点,(1)求∠AQB;(2)略.

当a2=6,b2=4,x0=0,y0=−2,直线BD过定点(0,1)时,据结论4(2)的充分性,得=(0,1)⇒λ=−2⇒k1k2=−2.

这就是如下2013年卓越联盟自主招生试题第(2)小题的结论:设椭圆的离心率为斜率为k的直线过点E(0,1)且与椭圆交于C,D两点.(1)求椭圆方程(答案:椭圆方程为(2)设A为椭圆的下顶点,kAC,kAD分别为直线AC,AD的斜率,证明:对任意的k,恒有kAC ·kAD=−2.

当a2=4,b2=1,x0=0,y0=1,λ=1时,据结论4(2)的必要性,得直线BD过定点

这就是2019年全国高中数学联赛广西赛区预赛试题第12 题第(2)小题的结论:如图2,设k＞0 且1,直线l:y=kx+1 与l1:y=k1x+1 关于直线y=x+1 对称,直线l与l1分别交椭圆于点A,M和点A,N.(1)求kk1的值(答案:kk1=1);(2)求证:对任意的k,直线MN恒过定点.

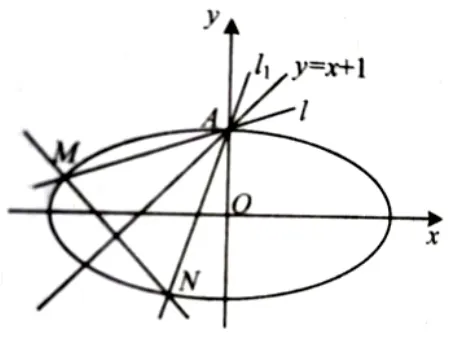
图2