不同“元”视角下两道最值问题的求解
2020-08-10安徽省濉溪县第二中学235100
安徽省濉溪县第二中学(235100) 祝 峰
数学问题求解时,常称一些研究对象为“元”.方程、代数式、函数中,把具有固定结构的可变对象视为一个“元”,如一元二次方程、二元代数式、多元函数即是基于这种认识所赋予的称谓.多元变量最值问题求解中,应多视角认识和构造“元”,否则会影响问题求解的灵活性、速度和正答率.下文是不同“元”视角下两道最值试题的灵活解答,旨在拓宽类似问题求解中“元”的认识视角.
1.例题
例1已知:正数x,y满足x+2y−xy=0,则x+2y的最小值为____.
例2在锐角三角形ABC中,若sinA=2 sinBsinC,则tanAtanBtanC的最小值为____.
2.“元”的相对视角
一般情况下,把一个独立量视为一个“元”.如例1 中,视x,y分别是两个元,则x+2y−xy=0 为二元二次方程、x+2y为二元一次代数式.但“元”不一定是一个独立的量,结构固定的代数式均可视为一个元.下面是更广视角“元”的认知下,两道例题的求解方法.
2.1 例1 的两种解法
解法一因为x+2y−xy=0,所以x+2y=xy=即(x+2y)2≥8(x+2y),所以x+2y≥8 或x+2y≤0(舍),即(x+2y)min=8(当且仅当x=2y取到).
解法二x+2y−xy=0,有x+2y=xy,注意到所以x2y2≥8xy,即xy≥8 或xy≤0(舍).(x+2y)min=8(当且仅当x=2y取到).
评析方法一中,基于x+2y范围的求解,视其为一个“元”,条件中xy是“多余”的,用基本不等式将等量关系消元为关于x+2y的一元二次不等式,求出其最小值;方法二中,由于x+2y=xy,若能求出xy的取值范围,即为x+2y的范围,所以视xy为一个“元”,则x+2y是“多余”的,需要消去.可以看到“元”是相对的,问题求解中,“元”不一定是一个独立量,也不一定是某个确定代数式.不同的“元”视角下会有相应的问题求解思路.
2.2 例2 的解答
三角形ABC中,若 sinA=2 sinBsinC,即sinBcosC+cosBsinC=2 sinBsinC.所以tanB+tanC=2 tanBtanC.由于在三角形中
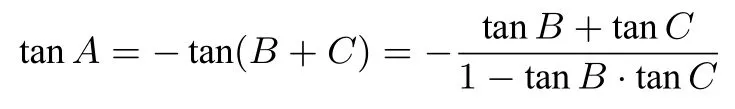
成立,所以
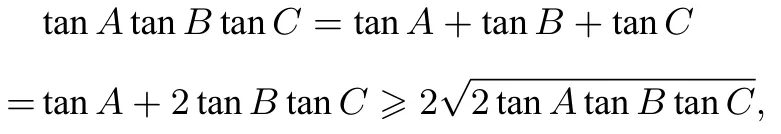
即
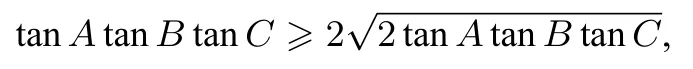
得tanAtanBtanC≥8(当且仅当tanA=2 tanBtanC取等号).所以tanAtanBtanC最小值为8.
评析注意到三角形中tanAtanBtanC=tanA+tanB+tanC成立,视所求范围量tanAtanBtanC为一个“元”,这种视角下,实际上可以直接按如下方式构建tanAtanBtanC的不等关系:
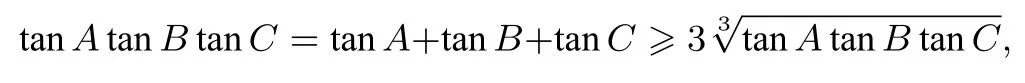
故tanAtanBtanC≥但只有tanA=tanB=tanC时才能取到等号,这与题设中sinA=2 sinBsinC矛盾,所以最小值取不到.
在此认识基础上,结合题设得到的tanB+tanC=2 tanBtanC,发现tanA+tanB+tanC=tanA+2 tanBtanC.再一次审视等式tanAtanBtanC=tanA+2 tanBtanC,将tanA和tanBtanC各视为一元,用二元基本不等式,问题获得解答.所以,对“元”的认识应该更广视角,其具有相对性,只有深刻理解,才能把握其本质.应鼓励学生,依据不同情境中的数量关系和变化规律,按着问题解决的需要,用自己独特的视角抽象出利于问题解决的变化因素.
3.“元”的绝对视角
把独立的变量视为一个“元”,是我们对元的初始认知,请看下面的解法.
3.1 例1 解法三
因为x+2y−xy=0,所以注意到x>0,有y>1.则y ∈(1,+∞),所以y=f(x)在(1,2)内递减,在(2,+∞)内递增,f(y)min=f(2)=8,即x+2y最小值为8.
3.2 例2 解法二
因为tanAtanBtan而sinA=2 sinBsinC,所以tanAtanBtan
注意到cosA=−cos(B+C)=sinBsinC−cosBcosC.所以,cosBcosC=sinBsinC−cosA=则有 tanAtanBtanC=f(A)=又tanAtanBtanC>0,所以tanA−2>0,而(当且仅当tanA=4 时取等号).
评析把每个独立的变量视为一“元”是多元变量问题解决的基本视角.常利用各元之间的相互关系,把多元变量转化为一元变量来解决.例1 中把二元变量x+2y变换为只含y的一元变量;例2 中把所求代数式tanAtanBtanC视为三元变量,三个元分别为tanA、tanB、tanC,充分利用它们之间的关系,消去tanB、tanC,把三元变量tanAtanBtanC变换只含tanA的一元变量,利用基本不等式,达到求解最小值的目的.
4.“元”的辩证视角
多元变量最值问题求解中,在对运算对象深入分析的基础上,确定“元”是运算思路产生的关键.合理运算思路下,灵活运用运算法则,即可做到心中无“元”胜有“元”,游刃有余地解决问题.
4.1 例1 解法四
因为x+2y=xy,所以所以
4.2 例2 解法三
由t=tanA+tanB+tanC=tanAtanBtanC,则
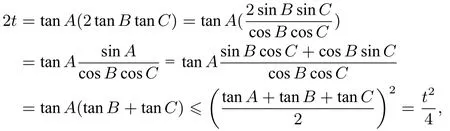
即t2≥8t,所以t≥8,当且仅当tanA=2 tanBtanC=4时取等号.
评析两个问题的求解中,并没有过多地从“元”的角度去思考问题,而是整体考虑多元变量之间的内在联系,从基本不等式的视角看问题,构造与多元变量相关的和或积是定值,来确定多元变量的最值.
多元变量最值问题中,变量之间的关系使得它们之间能够相互转化,这种转化在确定“元”时有重要意义.不同视角下,“元”可以是一个的独立变量,也可以是结构固定的多元代数式.问题求解过程中,辩证的“元”意识是灵活、快速、准确解决问题的关键.
