运用“半分离法”破解一类恒成立问题

浙江省宁波市第四中学(315016) 蒋亚军 魏定波

导数作为高考和模考中的压轴题,常考常新,学生普遍感觉解题困难、得分不易.针对频频出现以泰勒展开式为背景的一类恒成立问题,可以运用“半分离法”来优化破解这类问题.本文以追寻通法、方法运用和相关试题三部分来展开讨论.

1 追寻通法

试题呈现(2010年高考全国卷理科)设函数f(x)=ex−1−x−ax2,当x≥0 时,f(x)≥0,求a的取值范围.

试题背景本题是以ex的泰勒展开式为背景的试题,由于ex=1+x+当x≥0 时,ex≥1+x+所以,若x≥0 时有成立,则又当x≥0 时,f(x)≥0 也成立,所以,f(x)≥0 恒成立的a的取值范围是:

一般解法:f′(x)=ex−1−2ax,令g(x)=f′(x),g′(x)=ex−2a,当时,g′(x)≥0 在[0,+∞)上恒成立,所以g(x)在[0,+∞)上递增,g(x)≥g(0)=0,即f′(x)≥0(x ∈[0,+∞)),所以f(x)在[0,+∞)上递增,f(x)≥f(0)=0,所以符合题意.下面再证的必要性.

综上所得a的取值范围为

上述解法的原理是先“充分”后“必要”,但解题之中运用了二次求导,对学生来说,普遍感到困难.解题过程中,学生最容易想到变量a,x的分离,即而缺乏高等数学背景支持下,不易求出函数的最小值.实际操作中发现:由于[exf(x)]′=ex[f(x)+f′(x)],于是函数y=exf(x)的极值点研究可以在多项式函数中展开,为此,对这类问题提出一种便于学生操作的解法.

将f(x)≥0 变形为e−x(1+x+ax2)≤1,令F(x)=e−x(1+x+ax2)(x≥0),F′(x)=e−x[−ax2+(2a−1)x](x≥0).

当a＜0 时,由F′(x)=0,得x1=0,当时,F′(x)＜0,当时,F′(x)＞0,当x →+∞时,F(x)=e−x(1+x+ax2)→0,所以F(x)max=F(0)=1,即e−x(1+x+ax2)≤1 恒成立.

当a=0 时,F(x)=e−x(1+x),F′(x)=e−x(−x)≤0,所以当x≥0 时,F(x)≤1 恒成立.

当a＞0 时,若则当时,F′(x)＞0,则F(x)＞F(0)=1 与条件矛盾;若则当x ∈[0,+∞)时,F′(x)＜0,即e−x(1+x+ax2)≤1 恒成立.故

将ex−1−x−ax2≥0 变形为e−x(1+x+ax2)≤1 的方法称之为“半分离法”,下面结合高考和模考试题,说明该方法的运用.

2 方法运用

例1(2019 学年杭州市高三期末检测卷试题)设函数f(x)=ex+ax,x ∈R.若对任意的x ∈[0,+∞)均有2f(x)+3≥x2+a2,求实数a的取值范围.

解由2f(x)+3≥x2+a2,得e−x(x2−2ax+a2−3)≤2,令F(x)=e−x(x2−2ax+a2−3)(x≥0),

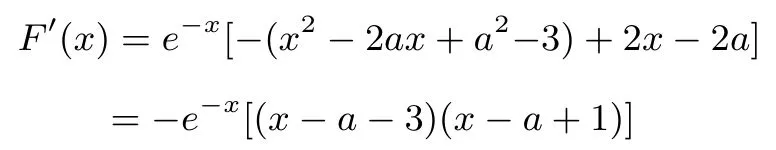
令F′(x)=0,得x1=a−1,x2=a+3.

(1)若a+3≤0,当x≥0 时,F′(x)≤0,即函数y=F(x)在[0,+∞)上单调递减,有F(x)max=F(0)=a2−3,依题意有a2−3≤2,此式无解.

(2)若a+3＞0 且a−1≤0,当x ∈(0,a+3)时,F′(x)≥0;当x ∈(a+3,+∞)时,F′(x)≤0,所以F(x)max=F(a+3)=6e−a−3,依题意有6e−a−3≤2,结合条件,解得ln 3−3≤a≤1.

(3)若a−1＞0,当x ∈(0,a−1)时,F′(x)≤0;当x ∈(a−1,a+3)时,F′(x)≥0,当x ∈(a+3,+∞)时,F′(x)≤0,所以

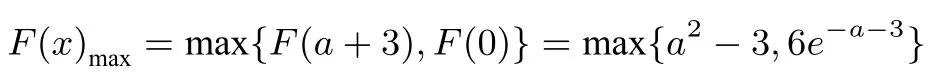
依题意有6e−a−3≤2 且a2−3≤2,结合条件,解得

例2(2019年浙江省丽水衢州湖州市高三(上)期末试题)已知a,b ∈R,f(x)=ex−ax+b,若f(x)≥1 恒成立,则的取值范围是____.

解由f(x)≥1 得:ex≥ax+(1−b),1≥e−x[ax+(1−b)],由指数函数和直线方程的图形可知a＞0,令

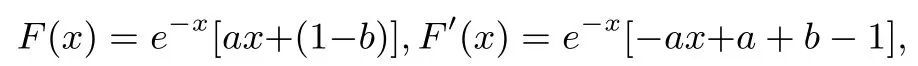
例3(2019 学年上虞高三期末统考试题)已知函数若f(x)≥−1 (其中a＞0),求a的取值范围.

解将f(x)≥−1,变形为1≥则

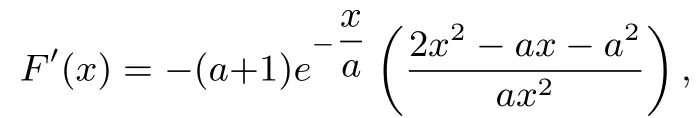
令F′(x)=0,由于x＞0,所以当x=a时,F(x)取得最大值.所以F(a)≤1,即解得:

例4(浙江省七彩联盟2018 学年高三期中试题)已知函数f(x)=x−xlnx,试证明:f(x)≤x2+e−x.

解将f(x)≤x2+e−x,变形为ex(x−x2−xlnx)≤1,令F(x)=ex(x−x2−xlnx),则F′(x)=−(x+1)ex(x+lnx),令F′(x)=0,则x+lnx=0,记x+lnx=0 的根为x0,由图象可知,当x ∈(0,x0)时,x+lnx＞0;当x ∈(x0,+∞)时,x+lnx＜0,所以

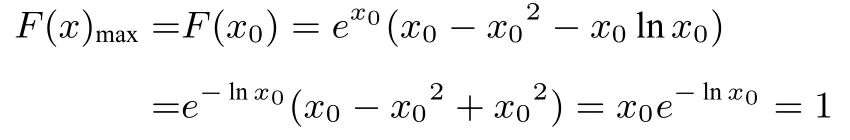
则ex(x−x2−xlnx)≤1,故f(x)≤x2+e−x成立.

3 相关试题

题目1(2019年绍兴市柯桥区高三期末试题)设函数f(x)=e−ax+2x(a≠ 0),当时,对任意x ∈(−∞,0],均有求a的取值范围.(答案:

题目2(2019年嵊州市高三期末试题)已知k ∈R,函数f(x)=ex−kx(其中e是自然对数的底数,e=2.718···),当x＞0 时都有f(x)＞x2+3x+2(k+1)成立,求整数k的最大值.(答案:−2)

题目3(2010年高考全国卷ⅠⅠ理科试题)设函数f(x)=1−e−x,设当x≥0 时,求a的取值范围.(答案:)

题目4(2012年高考新课标卷理科试题)已知函数f(x)满足

(1)求f(x)的解析式及单调区间;