高考中与向量交汇考题的分类例析
2020-08-10江苏省镇江市丹徒高级中学212143范习昱
江苏省镇江市丹徒高级中学(212143) 范习昱
向量不仅具有强大的工具性,广泛运用于函数、解析几何等高中重要知识,而且还具有很强大的兼容性,以向量为背景,命制的三角、函数、不等式、直线和圆以及圆锥曲线等解析几何综合题不仅新颖别致,而且富含数学思想和考验计算技能,得到很多命题者的青睐.
笔者翻阅分析各地大量高考数学试卷,选取与向量交汇的典型例题,分类例析,以飨读者.
1.向量与三角的交汇
例1(2015年高考广东卷理科第16 题)在平面直角坐标系xOy中,已知向量
(1)若m⊥n,求tanx的值;
(2)若m与n的夹角为,求x的值.
解(1)tanx=1,过程从略.(2)由于m与n的夹角为所以
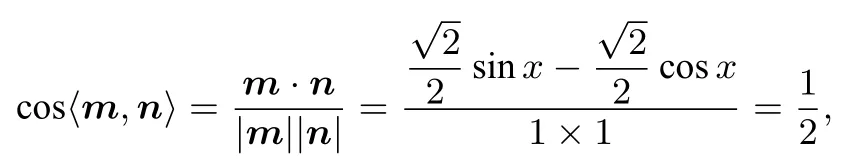
例2(2013年高考江苏卷第15 题)已知a=(cosα,sinα),b=(cosβ,sinβ),0<β<α<π.
(2)设c=(0,1),若a+b=c,求α,β的值.
解(1)略.(2)由于①2+②2得:所以,带入②得:
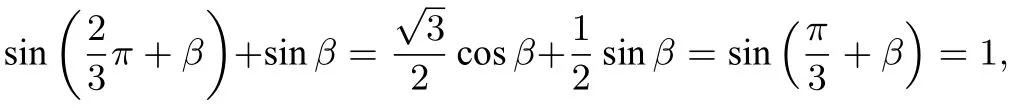
例3(2014年高考山东卷理科第16 题)已知向量a=(m,cos 2x),b=(sin 2x,n),函 数f(x)=a · b,且y=f(x)的图像过点和点
(Ⅰ)求m,n的值;
(Ⅱ)将y=f(x)的图像向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图像,若y=g(x)图像上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.
解(Ⅰ)过程从略.(Ⅱ)由(Ⅰ)知由题意知设y=g(x)的图像上符合题意的最高点为(x0,2),由题意知x20+1=1.所以x0=0,即到点(0,3)的距离为1 的最高点为(0,2).
将其代入y=g(x)得又因为0<φ<π,所以因此g(x)=2 sin=2 cos 2x.
由−π+2kπ≤2x≤2kπ,k ∈Z,得kπ,k ∈Z,所以f(x)的单调增区间为
例4(2014年高考辽宁卷理科第17 题)在∆ABC中,内角A,B,C的对边a,b,c,且a>c,已知−→BA·−−→BC=2,求:
(Ⅰ)a和c的值;
(Ⅱ)cos(B−C)的值.
解(Ⅰ)a=3,c=2,过程从略(Ⅱ)过程从略.
点评与反思向量与三角的交汇是各省市高考题中的常考题型,也是最受命题者青睐的中档难度的题型之一.以上几个案例基本覆盖了向量与三角交汇的所有题型,分别是向量与三角恒等变换交汇、向量与三角函数的图像与性质的交汇、以及向量与解三角形的交汇.解题基本策略是根据向量关系获得关于三角的方程或表达式,运用三角恒等变换的公式、三角函数图像和性质和正、余弦定理化简这些三角的方程或表达式即可.一般来说,让学生对照相应类型,然后注重一些易错细节,是可以攻克的.
2.向量与直线和圆的交汇
例5(2017年高考江苏卷第13 题)在平面直角坐标系xOy中,A(−12,0),B(0,6),点P在圆O:x2+y2=50 上,若则点P的横坐标的取值范围是____.
解设P(x,y),由得2x−y+5≤0,如图由2x−y+5≤0 可知,P在劣弧上,由解得M(1,7),N(−5,−5),所以P点横坐标的取值范围为
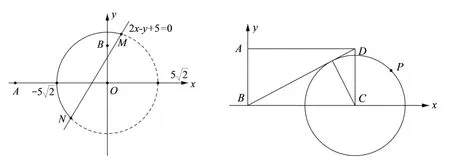
例6(2017年高考全国卷Ⅲ第12 题)在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若则λ+µ的最大值为( )
答案A,过程从略.
点评与反思第二类与向量交汇的考题就是在向量背景下的直线和圆,在各省市高考中也是经常出现,难度一般较大,有的甚至是压轴题.这类题的解题策略是利用解析法化简向量关系式,例如例5 中的“由得2x−y+5≤0”以及下文例7 中的“由得(x−x1.y0−y1)=λ(1−x,1−y0)”,脱掉向量的外套,便可迎刃而解.
3.向量与圆锥曲线的交汇
例7(2011年高考安徽卷理科第21 题)设λ>0,点A的坐标为(1,1),点B在抛物线y=x2上运动,点Q满足经过Q点与x轴垂直的直线交抛物线于点M,点P满足求点P的轨迹方程.
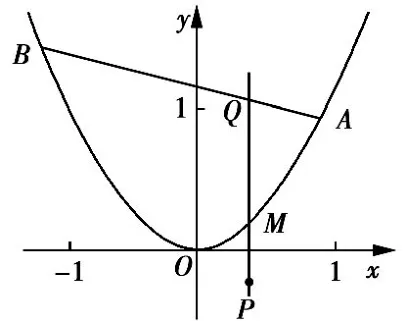
解由知Q,M,P三点在同一条垂直于x轴的直线上,故可设P(x,y),Q(x,y0),M(x,x2),则x2−y0=λ(y−x2),则
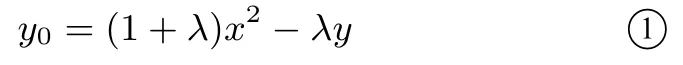
再设B(x1,y1).由得(x−x1.y0−y1)=λ(1−x,1−y0),解得
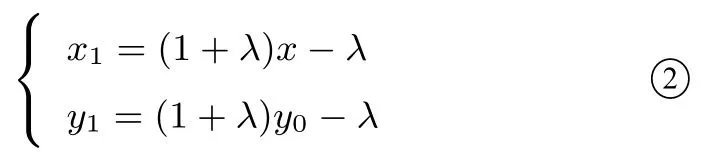
将①式代入②式得
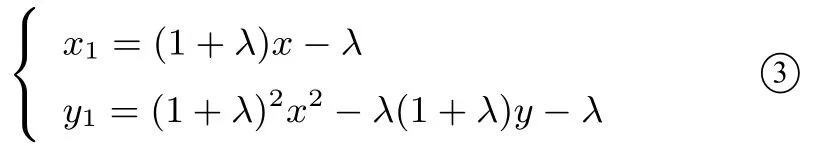
又点B在抛物线y=x2上,所以y1=x21,再将③式代入y1=x21,得
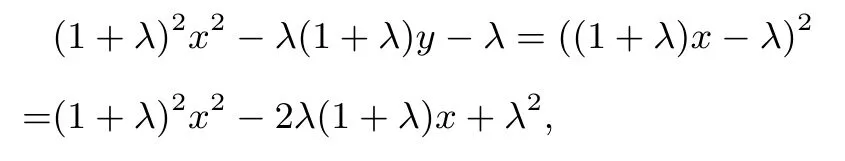
即有2λ(1+λ)x−λ(1+λ)y−λ(1+λ)=0,因λ>0,得2x−y−1=0.故所求点P的轨迹方程为y=2x−1.
例8(2013年高考湖南卷理科第21 题)过抛物线E:x2=2py(p>0)的焦点F作斜率分别为k1,k2的两条不同的直线l1,l2,且k1+k2=2,l1与E相交于点A,B,l2与E相交于点C,D.以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为l.
(Ⅰ)若k1>0,k2>0,证明:
(ⅠⅠ)若点M到直线l的距离的最小值为求抛物线E的方程.
解(1)由题意,抛物线E的焦点为直线l1的方程为由得x2−2pk1x−p2=0.
设A(x1,y1),B(x2,y2),由韦达定理可知x1+x2=2pk1,从而y1+y2=k(x1+x2)+p=2pk21+p.所以点M的坐标为从而
同理可得点N的坐标为(pk2,pk22).于是=p2(k1k2+k21k22).由题设,有k1+k2=2,k1>0,k2>0,k12,所以0<k1k2<故
(2)抛物线E的方程为x2=16y,过程从略.
点评与反思第三类与向量交汇的考题就是在向量背景下的圆锥曲线,在各省市高考中也是经常出现,难度很大,有的甚至是压轴题,其中蕴含繁杂的计算和思维推理.这类题的解题策略依然是利用解析法化简向量关系式,例如例7 中的两个线性关系都需用坐标等解析化的手段脱掉向量的外套,回归解析几何的“点差法”思想获得求解.
4.向量与不等式的交汇
例9(2016年高考浙江卷第15 题)已知向量a,b,|a|=1,|b|=2,若对任意单位向量e,均有|a·e|+|b·e|≤则a·b的最大值是____.
解由题意令e=(1,0),a=(cosα,sinα),b=(2 cosβ,2 sinβ),则由|a·e|+|b·e|≤可得
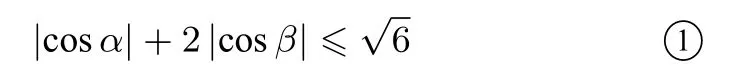
令
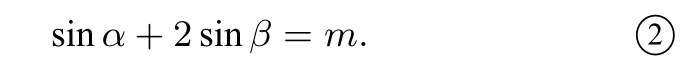
①2+②2得4|cosαcosβ|+4 sinαsinβ≤1+m2对一切实数α,β恒成立,所以4|cosαcosβ|+4 sinαsinβ≤1,
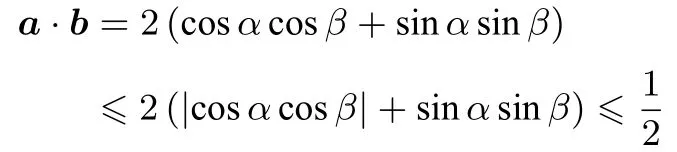
故a·b最大值为
例10(2015年高考天津卷理科第14 题)在等腰梯形ABCD中,已知AB//DC,AB=2,BC=1,∠ABC=60◦.动点E和F分别在线段BC和DC上,且则的最小值为____.
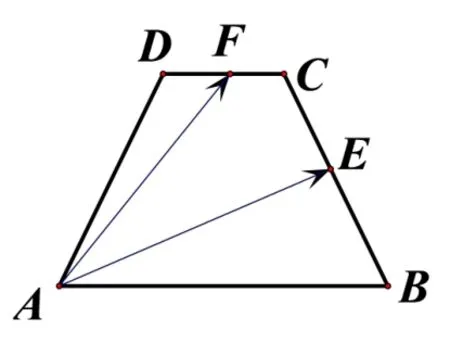
解因为所以
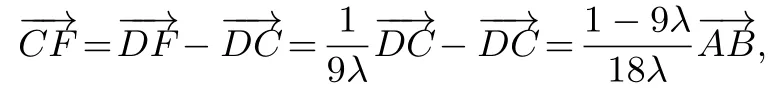
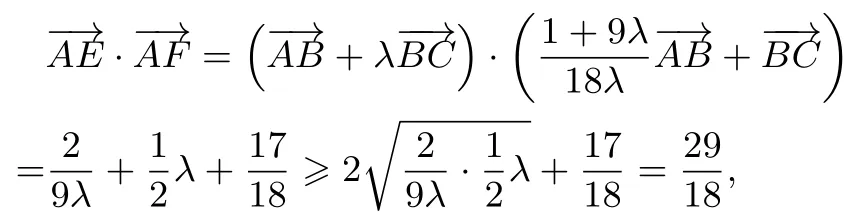
点评与反思不等式借壳向量也是极容易命制一些高质量大难度的综合题,一些省市高考中的填空或者选择压轴题中时有出现.其解题的基本策略是首先利用向量的基本计算化简含有向量的不等式或方程,然后回归不等式以及变量处理的框架解决.
5.向量与函数的交汇
例11 (2018年高考天津卷理科第8 题)如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120◦,AB=AD=1.若点E为边CD上的动点,则的最小值为( ).
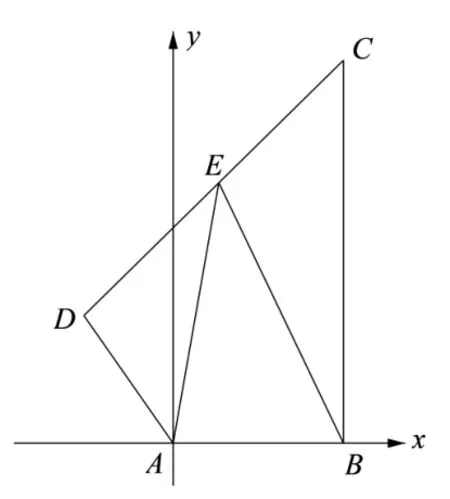
解以A为坐标原点,AB所在直线为x轴,建立如图的平面直角坐标系,因为在平面四边形ABCD中,AB=AD=1,∠BAD=120◦,所以A(0,0),B(1,0),所以
因为AD⊥CD,所以即解得即因为E在CD上,所以由kCE=kCD,得即因为所以
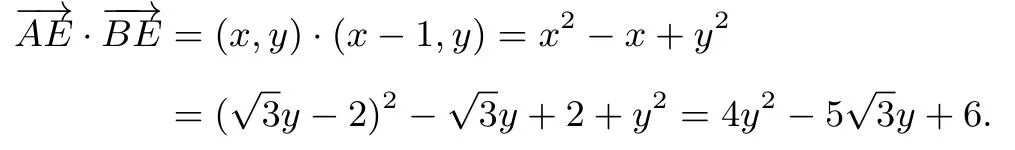
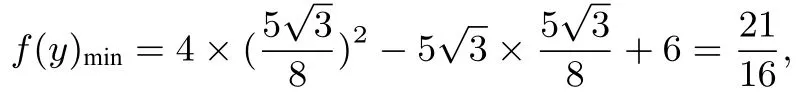
例12(2017年高考全国卷Ⅱ第12 题)已知∆ABC是边长为2 的等边三角形,P为平面ABC内一点,则的最小值是( ).
A.−2 B.C.D.−1
答案B,过程从略.
点评与反思函数是高中数学的核心内容,也是高考的核心考点,函数思想也是高中数学运用最为广泛的解题指导思想之一.穿上向量的外套,函数变得异常隐蔽,使函数的考查更有新意,这对学生的综合能力提出了很高的要求.其解题策略一般是利用向量的坐标运算比如数量积获得函数的“真身”,然后研究函数的性质、求解最值即可.值得注意的是,建系利用解析法是这类题最简单的做法,同时要注意采用数形结合的思想,消除思维认识上的不足.
6.向量与数列的交汇
例13(2015年江苏高考第14 题)设向量ak=则ak+1)的值为____.
解
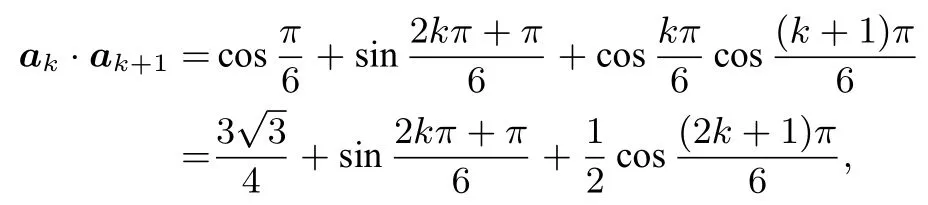
点评与反思 对于向量与数列的交汇的问题,一般二者的嵌入点是向量的坐标,通过向量的平行或垂直的坐标表示,将数列的基本要素比如通项、项数、首项或者前n 项和嵌入其中,达到整合二者的目的.其基本解题策略还是通过向量的坐标计算,脱掉向量的外衣,获得数列的递推关系,利用数列的知识求解其通项或者达到求和的目的.
结束语与向量交汇的高考题还要其他类型,以上六种是最为常见和重要的.通用的策略是转化题中向量的关系以获得方程、不等式或者函数关系式,扫除向量带来的干扰,最终解决问题.
