一个三角不等式的探究
2020-08-10广东省佛山市实验中学528300谢伟帆
广东省佛山市实验中学(528300) 谢伟帆
1 试题呈现
题目(2019年高考全国Ⅰ卷文科第20 题)已知函数f(x)=2 sinx−xcosx−x,f′(x)为f(x)的导数.
(1)略;(2)若x ∈[0,π]时,f(x)≥ax,求a的取值范围.
2 分析思考
第2 问求出a的取值范围是(−∞,0],整理不等式得x ∈[0,π]时,2 sinx−xcosx≥(a+1)x.根据笔者的经验,求参数范围的题目参数的临界值往往是相切的状态,当a=0 时,不等式为2 sinx−xcosx≥x,从而笔者思考,y=x是函数g(x)=2 sinx−xcosx的切线吗?这个不等式能不能推广?x的取值范围必然影响参数a的取值,能找到两者的关系吗?
3 模型建立
推理一y=x是函数g(x)=2 sinx−xcosx在x=0处的切线.
实际上,g′(x)=2 cosx−(cosx−xsinx)=cosx+xsinx,g′(0)=1,g(0)=0,所以g(x)在x=0 处的切线为y=x.果不其然,参数临界值是相切的状态.那么不等式能推广吗? 通过观察猜想,笔者建立了不等式模型asinx−xcosx≥(a−1)x.由于y=asinx−xcosx,y=(a−1)x均为奇函数,因此在研究时只需研究x≥0 的情况,下面对参数a进行分类讨论.
推理二若a≤0,则asinx−xcosx≥(a−1)x在[0,+∞)恒成立.
实际上,因为cosx≤1,x≥0,所以−xcosx≥−x,又由于sinx≤x,a≤0,所以asinx≥ax.因此asinx−xcosx≥ax−x=(a−1)x.
下面考虑a>0,x ∈[0,+∞)的情况.
推理三若a≥3,不存在区间[0,m](m>0),使得asinx−xcosx≥(a−1)x成立.
实际上,令h(x)=asinx−xcosx−(a−1)x,则asinx−xcosx≥(a−1)x等价于h(x)≥0.h′(x)=(a−1)(cosx−1)+xsinx.因为h(0)=0,h′(0)=0,要存在区间[0,m](m>0)使h(x)≥0 成立,则所以利用洛必达法则
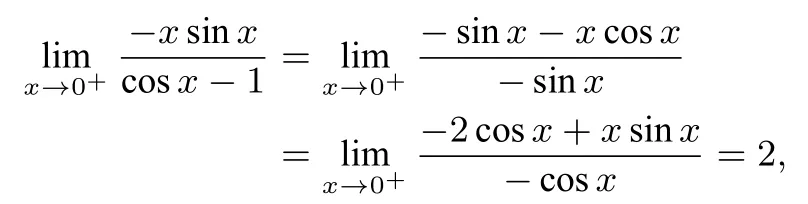
所以a<3,反之a≥3,则不存在区间[0,m](m>0)使h(x)≥0 成立.
推理四“0<a<3”是“存在区间[0,m](m>0),使得asinx−xcosx≥(a−1)x成立”的充要条件,且a的值与m的最大值一一对应.
实际上,由推理三的证明可知存在区间[0,m](m>0)使h(x)≥0 成立的充要条件是0<a<3.令h(x)=asinx−xcosx−(a−1)x,当h(x)=0 时,令下证F(x)在(0,2π)单调递减.
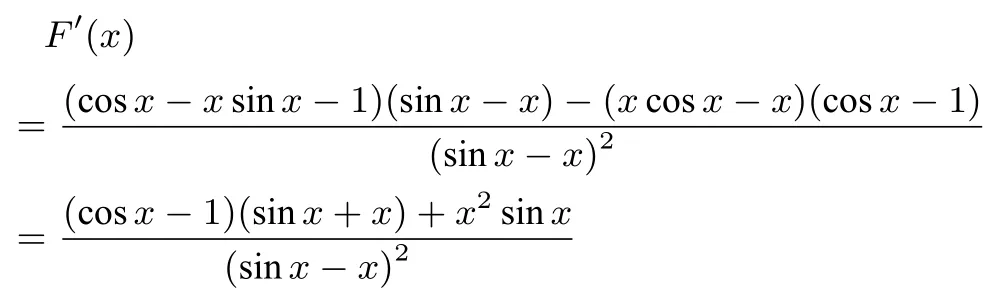
令G(x)=(cosx−1)(sinx+x)+x2sinx,其中cosx−1<0,sinx+x>0,所以(cosx−1)(sinx+x)<0.
①当x ∈[π,2π),sinx≤0,x2sinx≤0,所以F′(x)≤0.
G′′(x)=(3x−4 sinx)cosx+(1−x2)sinx.因为x ∈所以>4>4 sinx,(3x−4 sinx)cosx<0,(1−x2)sinx<0,所 以G′′(x)<0,G′(x)单调递减,所以G(x)单调递减,所以F′(x)<0.
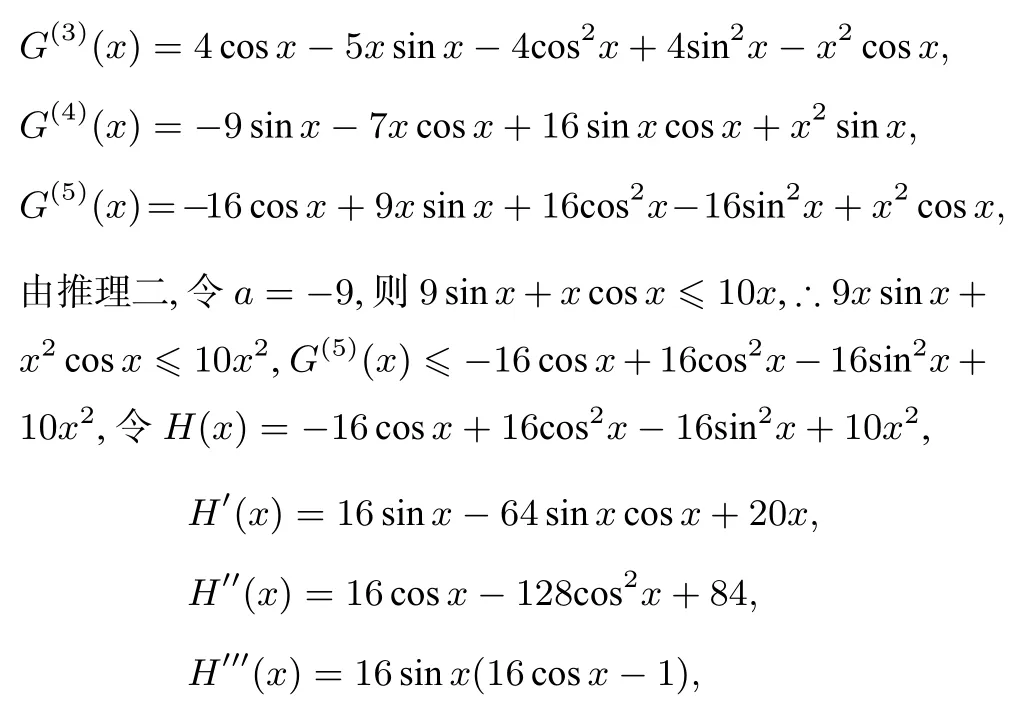
④当x ∈x2sinx≤x2,所以G(4)(x)≤−9 sinx−7xcosx+16 sinxcosx+x2,令I(x)=−9 sinx−7xcosx+16 sinxcosx+x2,则I′(x)=−16 cosx+7xsinx+16cos2x−16sin2x+2x,因为xsinx≤x,所 以I′(x)≤−16 cosx+9x+16cos2x−16sin2x.
令J(x)=−16 cosx+9x+16cos2x−16sin2x,J′(x)=16 sinx+9−64 cosxsinx,J′′(x)=16 cosx+64(sin2x−cos2x)>0,所以J′(x)递增,所以存在J(x)在递减,在递增,所以J(x)<0,即I′(x)≤J(x)<0,I(x)单调递减,所以所以G(4)(x)≤I(x)<0,G(3)(x)递减,同理,所以F′(x)<0.
综上可知F′(x)<0 在(0,2π)恒成立,F(x)单调递减,利用洛必达法则
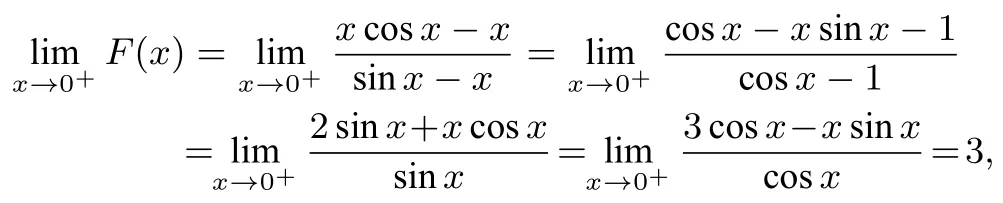
F(2π)=0,所以x ∈(0,2π)与a ∈(0,3)一一对应,即对于一确定的a1∈(0,3),可以在(0,2π)找到对应的x1,使得即找到了h(x)=0 的第一个正根x=x1.下证x1为m的最大值.由于
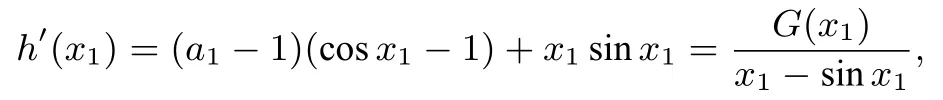
由G(x)<0 在(0,2π)恒成立知h′(x1)<0,所以存在δ>0,当x ∈(x1,x1+δ)>0,h(x)<h(x1)=0,所以m的最大值为x1,显然当m取(0,x1)的任一值时,不等式成立.
4 模型应用
对于2019年高考全国Ⅰ卷文科第20 题第二问:求x ∈[0,π]时,2 sinx−xcosx≥(a+1)x成立时a的取值范围,利用推理四,应用模型a1sinx−xcosx≥(a1−1)x,取a1=2,得2 sinx−xcosx≥x,利用求出x1=π,即不等式成立区间[0,m]中m的最大值为π,从而得到结论2 sinx−xcosx≥x在[0,π]恒成立,所以a≤0.题目设置的区间[0,π]已经是不等式成立的最大区间了!
5 反思总结
我们对不等式asinx−xcosx≥(a−1)x已经有了深入的认识,本质上是用切线逼近函数y=asinx−xcosx,在上述证明过程中有不等式G′(x)=x2cosx+xsinx−2sin2x<0 在(0,2π)恒成立,即事实上这里蕴藏着不等式有兴趣的读者可以进行进一步探究.
