基于混沌理论的弧形闸门面板振动特性研究

杨佼佼，徐国宾

(天津大学 水利工程仿真与安全国家重点实验室，天津 300354)

1 研究背景

弧形闸门作为水工建筑物中重要的组成部分，广泛应用于高水头的挡水建筑物[1-3]。对于弧形闸门的振动问题，国内外学者从原型观测、模型试验及数值模拟多方面进行了探讨[4-5]，但国内外失事的闸门案例中，很多都是由于脉动压力研究的不够深入所导致的。胡木生等[6]、李明[7]、温承永等[8]、李小超等[9-10]已从原型观测、数值模拟、数值模拟结合原型观测实验以及模型试验对弧门脉动压力进行分析等方面进行了研究。但对其振动的复杂程度没有进行系统的、理论层面的分析研究。

混沌理论已在多种振动研究中得到应用，如杨弘[11]在二滩水电站水垫塘底板的振动响应研究中，分别计算了混沌特征值的盒维数与关联维数，并发现其与水垫塘底板的振动无明显相关；罗贝尔[12]在研究高速水流与流激振动问题时，应用了混沌理论，并得出实际工程混沌特性的分析。本文采用混沌理论，通过对弧形闸门面板模型试验的振动时间序列进行处理，分析混沌特征值，指出弧形闸门面板的振动特性，分析了闸门振动情况的复杂性，为实际工程中闸门在复杂工况时的正常运行提供了理论支持。

2 相空间重构与混沌特征值

为研究弧形闸门面板振动的问题，运用混沌理论分析试验测得脉动压强时间序列，首先采用五点三次平滑法对数据进行降噪处理，然后进行相空间重构。通过重构的相空间，推求表征混沌系统的特征值，判断该时间序列是否具有混沌特征，并分析时间序列的复杂性[13-15]，进而研究弧形闸门面板振动的复杂性。

2.1 相空间重构

本文采用具有良好抗噪能力的互信息法来确定时间延迟τ[17]，通过构造平均互信息函数I(τ)：

(1)

绘出τ-I(τ)的图像，I(τ)取第1个极小值时所对应的τ即为最佳延迟时间。

通过平均伪最近邻域法——Cao方法来求嵌入维数，它对虚假邻点法进行了改进，且对处理含有噪声的时间序列具有极大的优势[17]。同时定义了E1(m)和E2(m)，E1(m)随m的增大而增大并趋近于1，取E1(m)等于1且不再变化时的m值为最小的嵌入维数。对于混沌时间序列，存在m使E2(m)不恒为1。同时计算E1(m)、E2(m)来确定嵌入维数。

2.2 混沌系统的特征参数

2.2.1 饱和关联维数 饱和关联维数是定量描述分形维数的数学量，它是从混沌吸引子中提取的一种维数，描述时间序列所代表的非线性动力系统的混沌程度，系统的关联维数越大，复杂度越大。

在重构相空间Yi={xi,xi+τ,…,xi+(m-1)τ}(i=1,2,…,(N-(m-1)τ);M=N-(m-1)τ)的基础上，定义[16]：

(2)

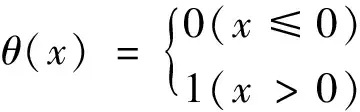
有混沌特征的序列满足C(r)∝αrD(r>0)，采用最小二乘法求lnr-lnC(r)图像中明显直线段的斜率即可得关联维数D。

2.2.2 Lyapunov指数 Lyapunov指数描述了相空间相邻轨道的平均发散(λ>0)或平均收敛(λ<0)的性质，若最大Lyapunov指数为正，可以判断该非线性动力系统具有发散特征，即为混沌系统，且其大小反映了系统的混沌程度。对含有一定噪声影响的较小数据，求其最大Lyapunov指数λ1可采用小数据量法来计算[18]。重构相空间后寻找每一相点的最近邻点，其距离为:

(3)

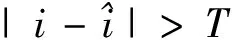
(4)

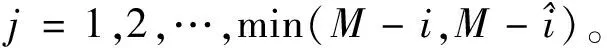
对于每个j求出所有非零lndi(j)的均值：

(5)

式中：q为非零lndi(j)的个数;ts为采样周期。绘出j-Zj图像，用最小二乘法进行拟合，其斜率即为最大Lyapunov指数λ1。

3 弧形闸门面板振动特性

3.1 弧形闸门模型试验与数据分析

本文以大石峡弧形工作闸门模型试验为例，孔口尺寸(高×宽)为4.5 m×6 m，弧面半径13 m，弧门面板厚30 mm，面板沿纵向布置为13根T形小横梁，小横梁腹板截面尺寸500 mm×20 mm，下翼板截面尺寸200 mm×30 mm。模型几何比尺为1∶25，在闸门面板中线布置了6个脉动压力传感器，采样频率为100 Hz，闸门水力学模型布置如图1所示。模型用专门研制的水弹性模型材料，其模型材料的门叶结构的刚度、重量及密度与原型一致为7 850 kg/m3，弹性模量为原型的1/25，即8 GPa。试验测试正常蓄水位1 700 m、校核洪水位1 701.3 m和汛期限制水位1 694 m时，在闸门4个开度，即4、8、12、16 cm，分别对应原型1、2、3、4 m开度共12种工况下的闸门面板脉动试验数据。试验测点布置如图2所示。试验过程中取各水位各开度下，每个测点60 s的数据进行分析。

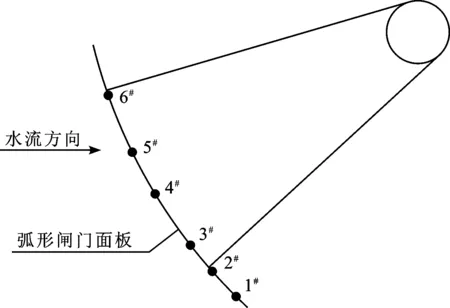
图2 弧门面板脉动压强观测测点布置图

图1 弧形闸门面板水力学模型及测点布置

3.2 面板脉动压强数据相空间重构

首先对观测数据进行降噪处理，然后由平均互信息法计算各测点不同开度时振动的加速度时间序列的延迟时间τ，根据计算所得的延迟时间τ，用Cao方法计算嵌入维数m。如图3为1 700 m水位下开度为16 cm时1#测点的计算过程图，其他各开度下其他测点的计算过程与此类似，其中图3(a)为τ与I(τ)关系曲线，图3(b)为E1(m)、E2(m)的计算曲线。由图3(b)可明显看出，E2(m)不恒为1，满足混沌条件可选取嵌入维数。表1所示为各测点计算所得的时间延迟τ和嵌入维数m。

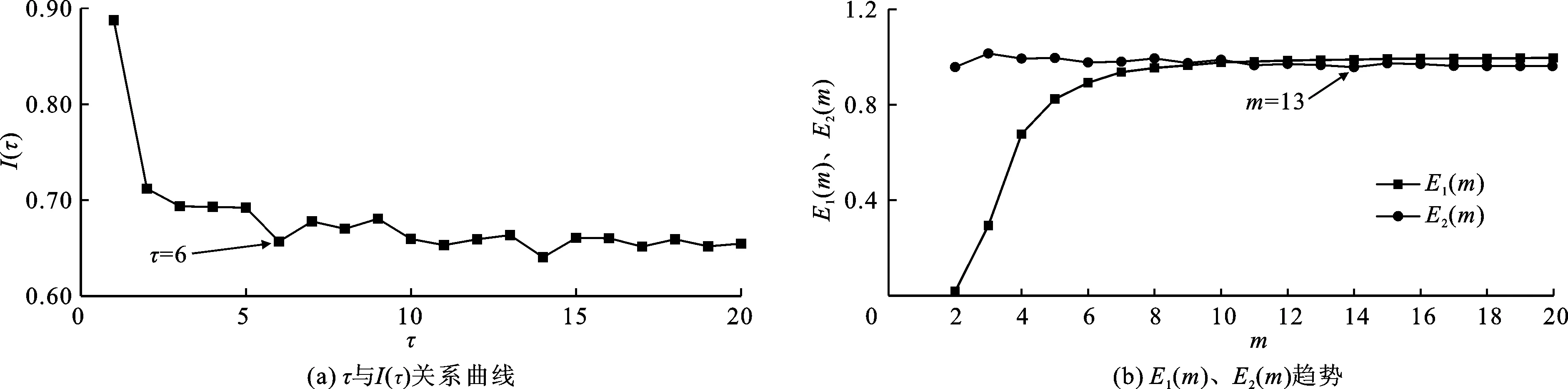
图3 正常蓄水位1 700m开度为16 cm时1#测点脉动压强时间序列τ与m计算示意图

表1 1#～6#测点脉动压强时间序列的τ与m表

3.3 关联维数与Lyapunov指数

3.3.1 关联维数 关联维数的计算要求由平均互信息法求得的τ，代入关联维数的计算中，并令m从2开始由小到大依次取值至20，由公式(2)计算绘出典型测点典型相对开度下lnr-lnC(r)的关系曲线，如图4(a)所示，其他测点计算图与此类似，对各条曲线明显直线段由最小二乘法求其线性回归斜率，其斜率与m值的关系如图4(b)所示。表2为1#～6#测点各开度与关联维数取值对应关系。

图4 典型测点脉动压强时间序列关联维数与m关系图

由表2分析可得：(1)总体分析，面板靠近底缘位置(测点1处)的关联维数较大，表明此处振动的复杂程度较大，由于闸下出流且为淹没出流的情况，会在闸后形成淹没水跃，在闸门底缘处产生较大的脉动压力，从而造成面板靠近底缘位置的振动情况较其他位置处更为复杂；(2)闸门面板大部分测点表现为：在小开度时(4 cm)呈现出较小的关联维数，即在闸门小开度时，建模运算过程中可通过较少的独立控制变量来实现闸门的非线性运算过程；(3)面板在4个开度下，与水面靠近的位置即开度12 cm时测点3位置、开度8 cm时测点4位置、开度4 cm时测点6位置关联维数均较大，可以看出闸门面板在与水面接触处振动情况更为复杂，气液固3项耦合处对闸门振动的影响较临近测点位置更大，可着重分析在靠近水面位置面板的受力变化。

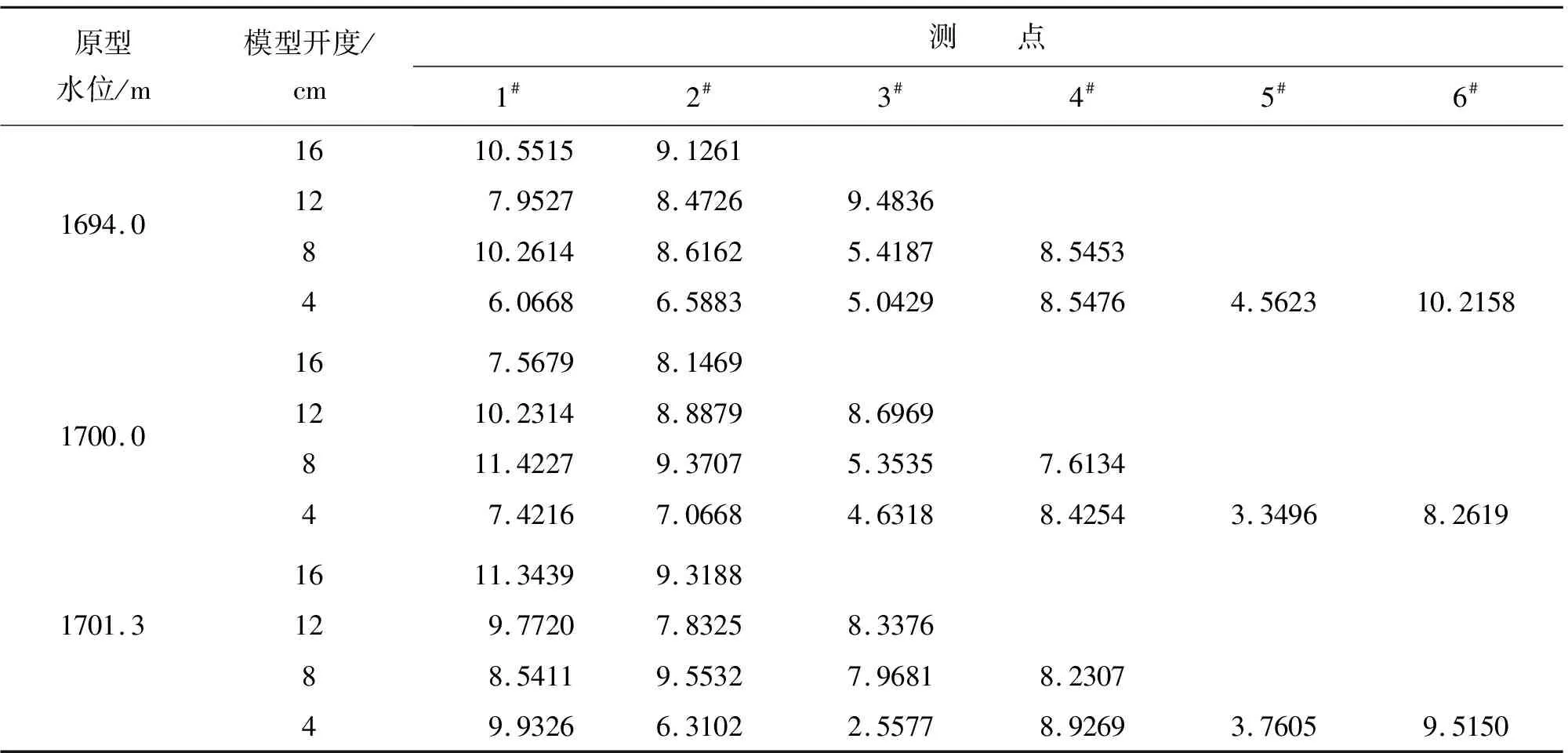
表2 1#～6#测点各开度的关联维数

3.3.2 Lyapunov指数 在相空间重构的基础上，由已确定的延迟时间τ、嵌入维数m，通过公式(3)～(5)来计算最大Lyapunov指数，图5所示为数据分析得到的j-Zj图像，对图像的前半部分，即增函数部分采用最小二乘法进行拟合，得到的斜率即为最大Lyapunov指数λ1。而之所以会出现后半段稳定不变部分，是由于重构相空间的混沌吸引子有界，λ1不会超过吸引子的界限。表3列出各测点的λ1值。

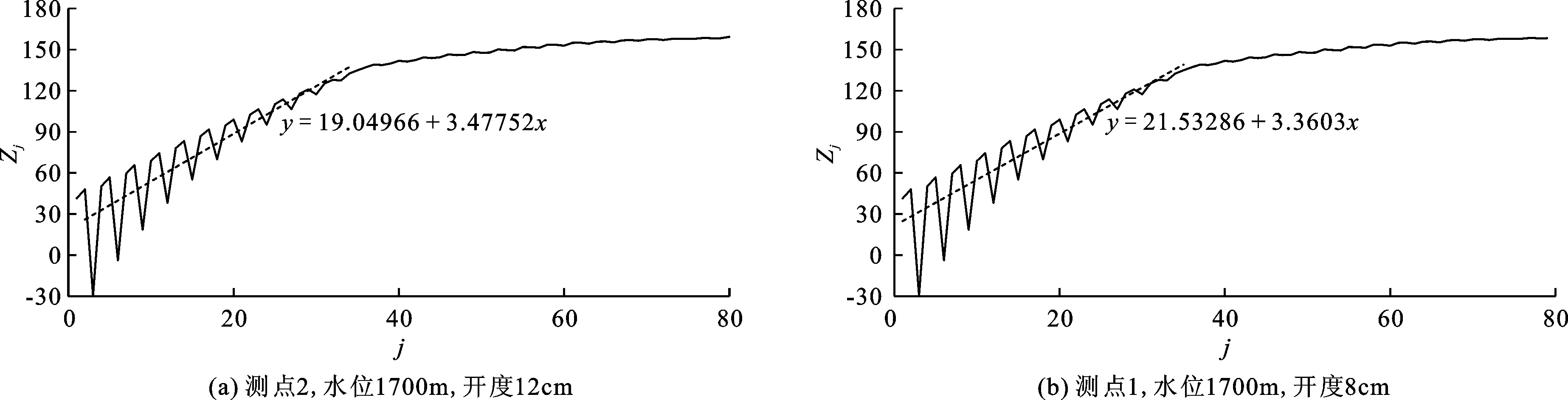
图5 典型测点Zj与步长j演化关系图

由表3分析可以看出：(1)闸门在较高水位时(1 700、1 701.3 m)，开度为8 cm处的λ1较其他开度时更大，说明其面板的振动复杂程度也更大；(2)在1 701.3 m水位时，弧形闸门面板在开度为4 cm时，除测点1外其他测点总体表现出的λ1值相对较低的两个水位更大，分析可知在高水位小开度时受到的水压力更大，在淹没出流的情况下由能量分析可知，在同样下游水位情况下，流体的能量更多地传递给闸门，故而造成面板有较复杂的振动情况；(3)测点1即最靠近闸门底缘位置处，在大开度时的λ1更大，可以看出闸门底缘过流量越大，其闸门面板的振动情况复杂程度越高。

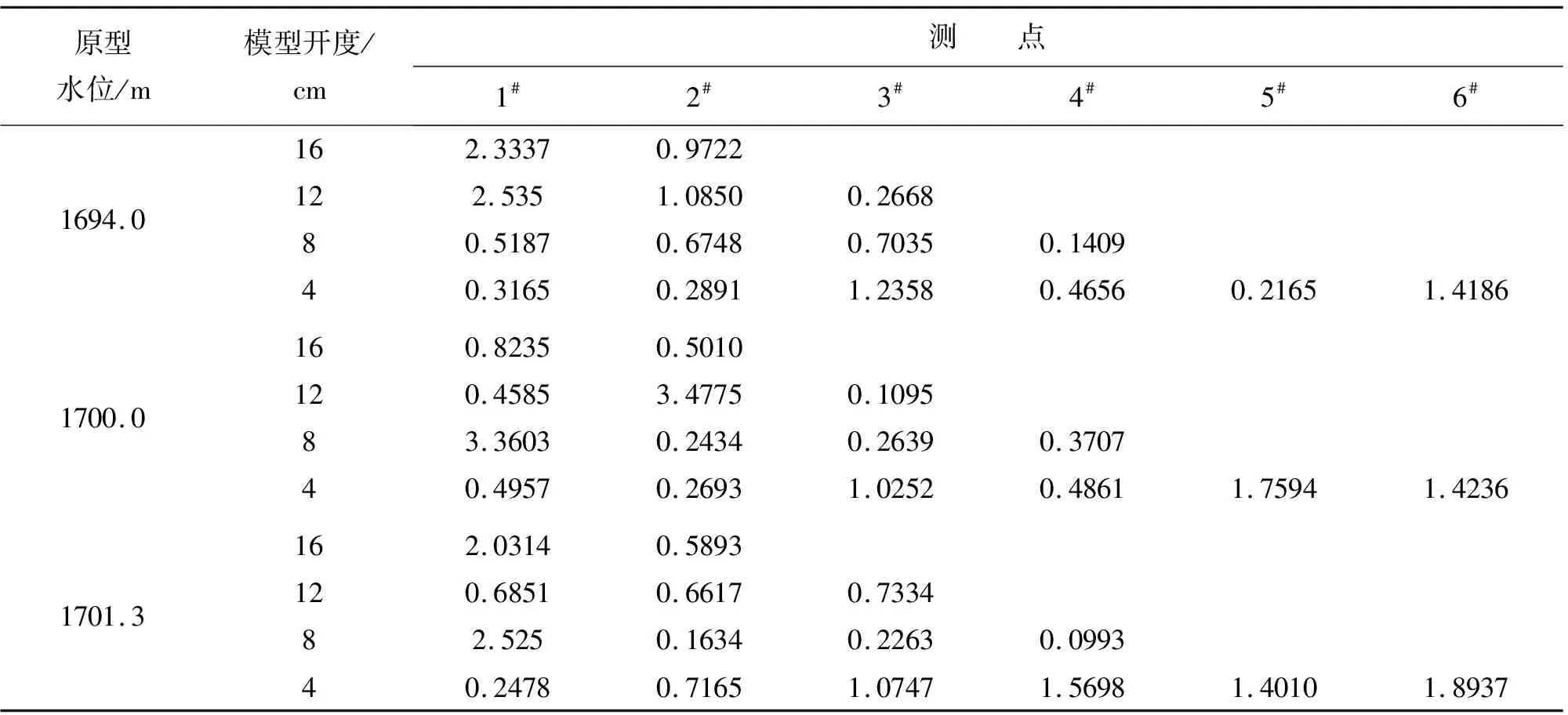
表3 1#～6#测点各开度最大Lyapunov指数λ1表

4 结 论

本文从混沌理论角度对弧形闸门面板的振动情况进行了研究，重点分析了其振动复杂程度的问题，并得出如下结论：

(1)由关联维数与Lyapunov指数分析得出，弧门面板振动复杂程度在大开度高水位下表现为更复杂；在闸门底缘位置的振动情况表现有更大的不可预测性，其复杂程度更高。

(2)弧形闸门小开度时，在闸门面板建模运算中的非线性振动情况可由较少独立变量进行控制，变量选取方法可进一步研究探讨。

(3)根据本文的相空间重构结果及Lyapunov指数的计算，为基于混沌理论进行弧形闸门面板振动情况的短期预测提供前提。