改进的混沌理论和BP神经网络化工产品需求预测模型设计

李永锋

(西安航空职业技术学院 现代教育技术中心，陕西 西安 710089)

随着中国“世界工厂”地位逐渐凸显，化工产品的个性化定制需求越来越多。如何精准预测化工产品需求，避免资源浪费，减少企业不必要的生产成本从而提高工业产品利润率显得尤为重要。

人工神经网络(artificial neural networks,ANN)是基于生物神经网络对信息进行自动优化的方法，该方法具有很高的容错性、鲁棒性及自组织性。虽然人工神经网络不能和生物神经网络等价，但在一些方面取得了优越的性能。当前，该网络已经广泛应用在了智能语言处理、人工智能等领域。

混沌时间序列在实际环境中广泛存在。所谓混沌时间序列，是指由混沌非线性动力系统产生的时间序列。其外在表现类似随机，对初值十分敏感，因此这类系统对长期预测十分困难，但内在的非线性动力学特性又是具有确定性的，这使得短期预测成为可能。

有学者利用多指标与卷积神经网络的化工产品需求预测；利用基于实验数据改进的人工神经网络进行学习训练，进行销售预测，将结果与未改进的人工神经网络和较先进的卷积神经网络和高斯混合模型以及销售公司的销售数据作比较，从准确率、召回率和F值3个指标分析改进人工神经网络的预测精度，能够较好地预测销售成交情况。还有通过GRU-BP组合神经网络预测模型，研究在不同时间序列上各型号产品相互制约影响下产生的不同需求形态；同时考虑产品自身属性差异、供应链环境等影响因素，可以预测出某型号产品未来一段时间内的需求量。为提高制造企业产品需求预测的精度，提出了产品数据空间和一维卷积神经网络——长短期记忆神经网络的深度学习算法，预测效果优于神经网络模型和单一的LSTM模型。为了克服关键质量变量测量滞后所带来的不利因素，提高氟化工过程先进控制系统的控制精度，提出了一种具有输入数据注意力机制的卷积神经网络用于产品质量预测。

针对目前研究的结果，本文提出了一种基于混沌理论相空间重构算法的BP神经网络化工产品需求预测模型，分析其发展趋势，构建其混沌系统相空间，利用BP神经网络深度学习算法模型，对未来产品需求进行预测，最后进行实验论证该方法的有效性与可行性。

2 方法框架

以某化工企业 2018年1月到2019年9月的202 种具体产品的需求订单作为数据源，利用混沌理论相空间重构算法计算其相空间的参数构建对应的相空间；然后将重构后的相空间作为BP神经网络的输入，使用更新数据集的方法，达到工业产品需求预测的目的。预测方法的框架如图1所示。

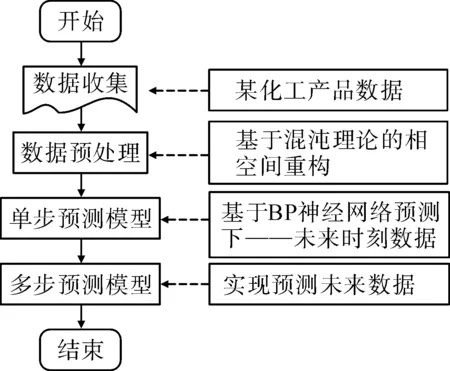
图1 化工产品需求预测方法框架图Fig.1 Framework of method for chemical products demand prediction

由图1可知，整个方法分为4步，即从数据收集、数据预处理和后续的单步预测模型以及过渡到最后的多步预测模型。在最重要的第3步，通过BP神经网络结合构造相关模型，可以很好地化工产品需求进行预测，方便后续对工厂生产做出及时调整。

2.1 数据获取

本文使用八爪鱼采集器软件实现了一个针对特定数据的爬虫。目标数据是某化工企业2018年1月到2019年9月的202 种具体产品的需求订单作为数据源。

2.2 混沌理论

首先，量子力学中的不确定性原理表明，如果想同时知道一个微观粒子的动量和位置，是永远不可能做到的，并且波函数证明了在没有进行测量的时候，微观粒子在空间当中的位置是服从概率分布的。举个例子，就目前来看人们还不能精准的去预测地震和天气预报，因为天气预报只能大范围的，短期的预测不是每次都很准。如果想要精准的预测，比如这片云要下雨，能落到哪一条街、哪个人身上，这肯定是做不到的。这一切的背后有一套理论在做支撑，叫做混沌理论。混沌状态区别于随机状态，这两种状态差异化很大。随机状态就是纯概率的事件，如掷骰子一般。而混沌系统，它虽然有解，但要解开难度极大，并且混沌系统总是在变化之中，它的状态稍微有一丁点系统内的变化到最后都有可能引起巨大的改变。

总而言之，混沌理论表明一切看似没有关系离散的事件，在其内部都有一定的联系。人们肉眼能观察到的，可能都是一个混沌系统的局部，所以看不到其联系，可见混沌系统暗含了混沌系统是具有局部随机整体有序的特点。随着混沌理论的深入研究，人们可能会解释或预测出某些事件现象的发展趋势。

2.3 重构相空间

相空间理论

在数学和物理领域，定义一个动力系统所有可能的状态空间，并且系统中每一个可能的状态都与唯一一点相对应。这些点的组合空间称作相空间，系统的每个变量可以用相空间中的一个维度来表示。动力系统的单个状态被称作相空间点的状态向量。将相空间中的点连接起来，就得到了系统的相空间轨迹，该轨迹反映了动力系统的状态随时间演化的过程。

重构相空间方法

一般来说，相空间是高维的。肉眼可见的时间序列往往都是整个动力系统的一维时间序列，称为单变量混沌时间序列见式(1)。

={:=1,2,…,}

(1)

式中：为时间长度；为第时刻的序列值。

重构相空间的坐标延迟法和导数重构法是由时序序列进行相空间重构得来的。由于导数重构法是需要对数值进行微分，所以该方法对数据的噪声十分明显。因此在实际应用中常采用坐标延迟重构法。

假设单变量混沌时间序列为式(1)所示，坐标重构法需要2个重要参数，延迟时间和嵌入维数。将时刻之后每个时刻的序列值插入到当前向量中，直到组成一个维向量，该向量就为重构相空间的第时刻对应的状态向量。

=(,+,+2,…,+(-1)),=1,2,…,

(2)

式中：=-(-1)，为重构相空间的所有状态数目。最后得到了重构后的相空间。

=(,,…,)

(3)

(1)自相关法选取延迟时间()。在重构相空间的实际运用中，延迟时间不能过大也不能过小，如果太小，那么重构相空间中的+(-1)与+会十分相近，使得重构相空间中的相邻状态向量相关性较强，无法表现出系统的动力特征。同理，如果太大，那么重构相空间的响铃状态向量相关性会十分小，使得简单的轨道看上去也会十分复杂。

实验中选择了自相关法来选取延迟时间，对于混沌时间序列，其自相关函数定义：

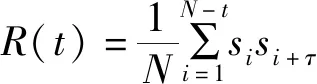
(4)

自相关法规定，当自相关函数的值()下降到初始值(0)的(1-1/e)倍时，所对应的的为合适的延迟时间值，但可以根据具体情形进行调节；

(2)Cao氏法选取嵌入维数()。Cao氏法是对虚假最近邻法的改进，其优点是只需要参数延迟时间。在重构相空间中，计算每两对状态点的欧氏距离，即：

,=|-|

(5)

将与扩展一维之后，再次计算其欧氏距离：

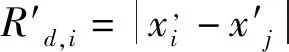
(6)

Cao氏法中，直接用′,与,的比值定义指标：

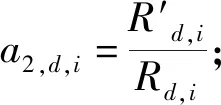
(7)

距离度量选择无穷范数，定义：

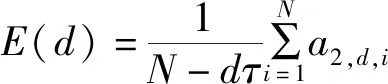
(8)

式中：()的值为总体的虚假近邻情况，当嵌入维数从变化到+1时，()的变化情况，定义：

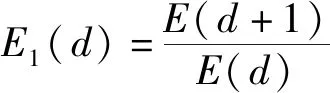
(9)

如果时间序列是具有混沌性的，那么()会在大于某个特定值后将趋于稳定，那么将该值作为嵌入维数是比较合适的。

2.4 BP神经网络预测模型

单步BP网络预测模型

单步BP网络预测模型，如图2所示。

图2 单步预测模型Fig.2 Single-step prediction model

由图2可以看出，依据状态序列的定义，相空间中最后一个状态向量为=(,+,+2,…,+(-1)),则对应的下一时刻的状态向量应为+1=(+1,+1+,…,+1+(-1))。因此，下一时刻的状态向量中只有最后一个分量+1+(-1)是未知的，这一分量也就是单步预测模型需要预测的下一时刻序列值。故单步预测模型需要在已有时序中预测出下一未来时刻的数据。

多步BP网络预测模型

多步BP网络预测模型，结果如图3所示。

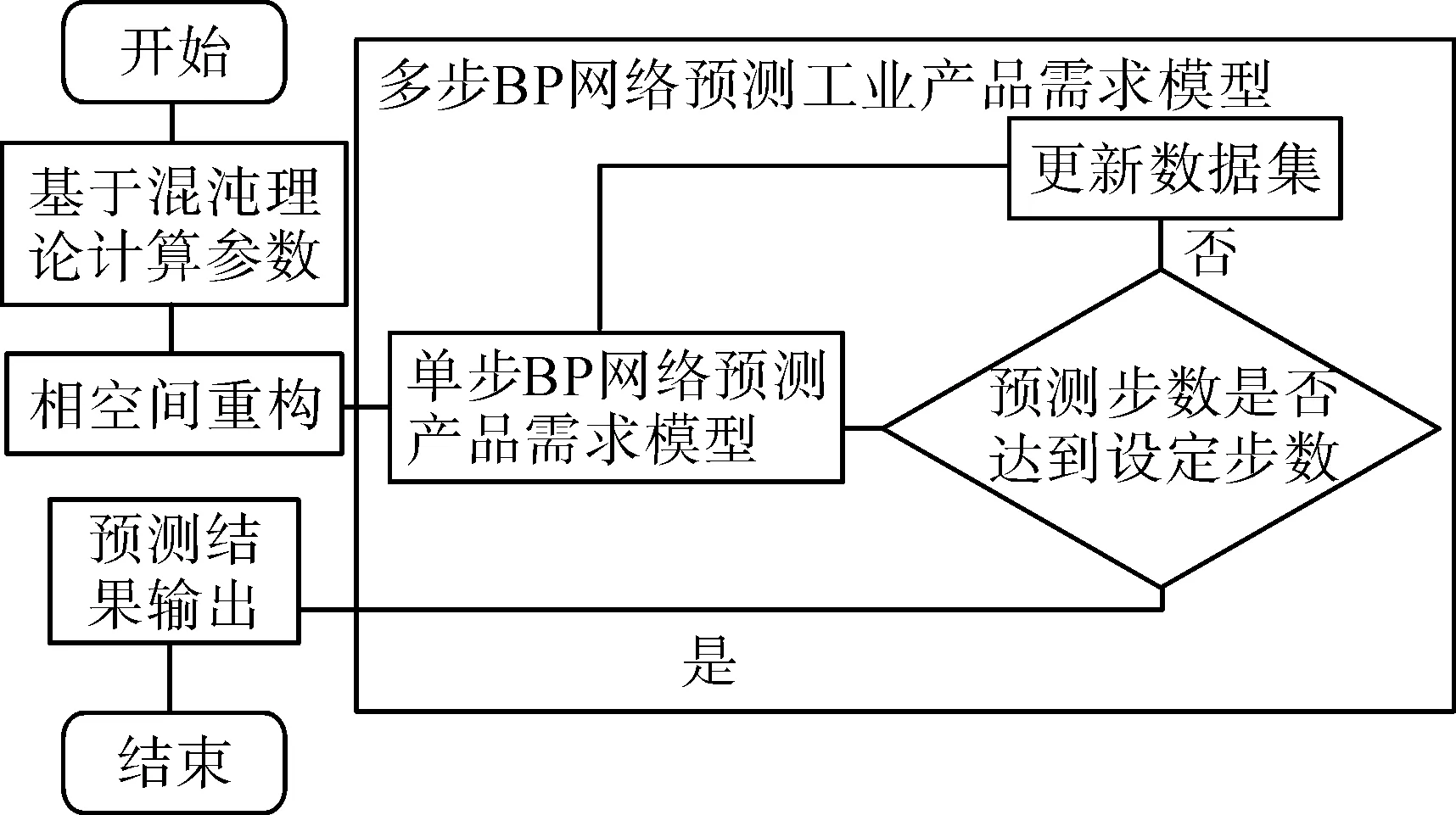
图3 多步预测模型Fig.3 Multi-step prediction model

由图3可以看出，多步预测模型是在单步的基础上，通过更新数据集的方法，实现多步预测的目的。多步预测方法是以预测值作为已知数据更新状态向量完成的，那么随着步数的扩大，理论上预测收益率误差会越来越大，所以该方法只能进行短期预测。

3 实验研究

3.1 实验工具

使用八爪鱼采集器收集数据，使用Python语言基于Tensorflow2.4.1构建模型。

3.2 数据集及处理

通过自相关法计算自相关函数()，选择其值约为(0)的(1-1/e)倍的值作为延迟时间，自相关函数随延迟时间变化情况如图4所示。

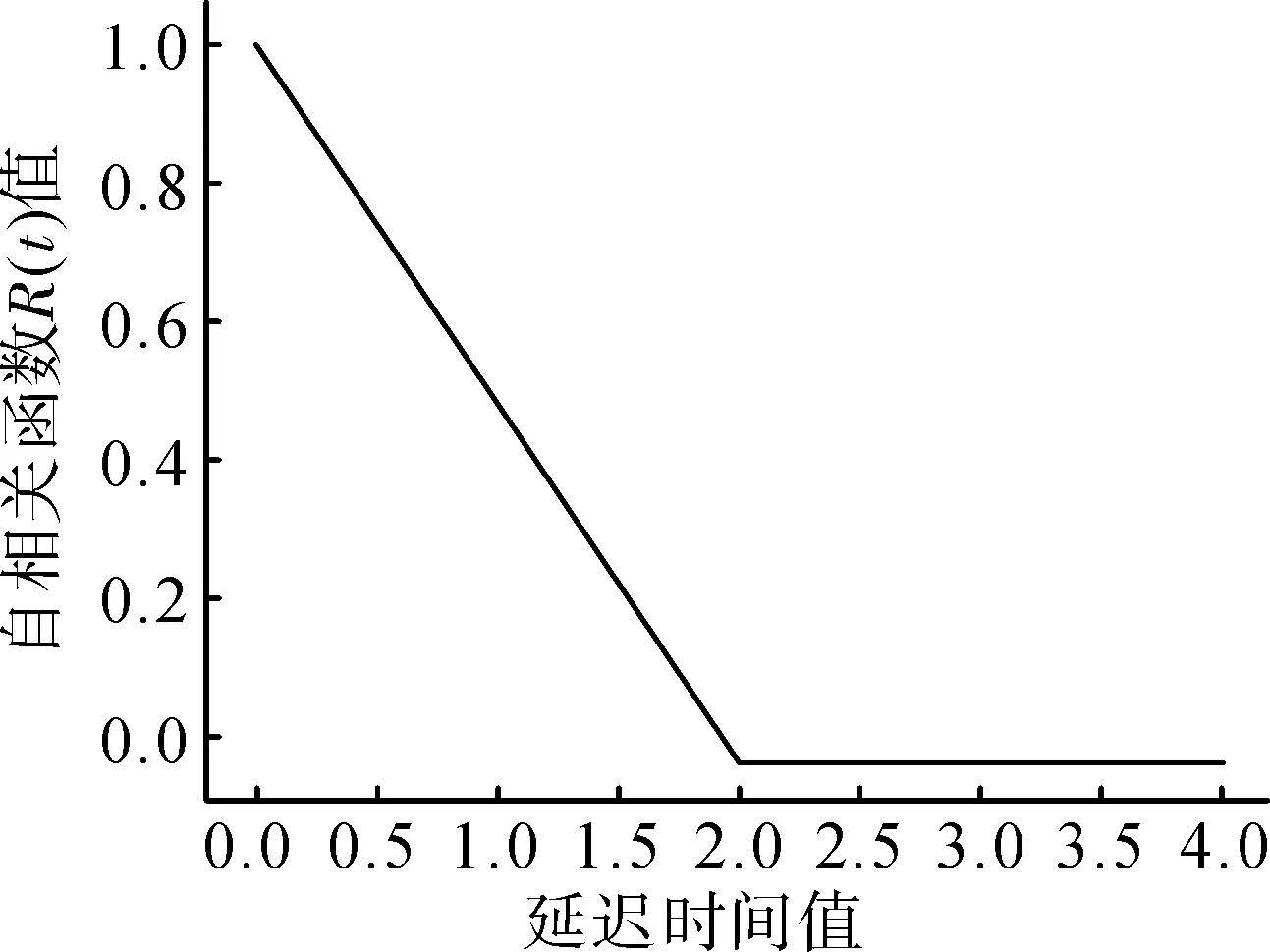
图4 自相关函数随延迟时间变化Fig.4 The varies of autocorrelation function with delay time

由图4可以发现，本次试验中为1是比较好的延迟时间。

使用Cao氏法计算时序的总体虚假邻近值()，再根据时序相邻点的邻近值比值()选择合适的嵌入维数；总体虚假邻近情况随嵌入维数变化情况，结果如图5所示。

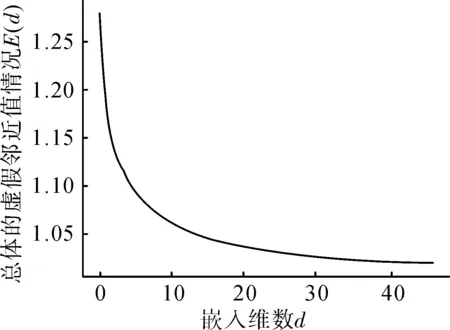
图5 总体虚假邻近情况随嵌入维数变化Fig.5 The varies of overall false proximity with embedding dimension

由图5可以看出，当延迟时间为1时，最佳嵌入维数为10。

3.3 化工产品需求预测实验

模型参数设置

数据集输入为时序序列构成的相空间，由“3.2”节得出，相空间的延迟时间为1，嵌入维数为10，状态向量一共有411个。选取某化工企业2018年1月到2019年9月的202 种具体产品的需求订单时序作为训练集，即选用相空间中前406个状态向量。BP神经网络模型学习率为0.01，激活函数选择tanh函数。通过实验对比，选择2层隐藏层每层选择15个神经元。反向损失函数选择均方误差，反向传播优化方法使用AdamOptimizer优化器。

模型训练与评估

根据“3.3.1”节的实验设计，评价指标有预测精度、相对误差和均方误差。实验结果表明，模型在未来两天的平均预测精度为90.87%，平均相对误差为9.13%，最小相对误差为1.19%，均方误差为0.001 5。虽然模型在未来两天后的预测精度不高，但依然具有预测趋势的价值。在预测实验中，预测模型平均预测精度大于90%，则说明模型预测效果良好。预测结果见图6。

图6 模型预测结果Fig.6 Results of model prediction

4 结语

本文基于混沌理论和4层BP神经网络进行化工产品需求预测。使用自相关法和Cao氏法来确定相空间参数，重构其相空间；通过实验确定BP神经网络隐藏层结点个数分别为15个时，预测精度较高。该预测模型在未来2 d的平均预测精度为90.87%，最高预测精度可达98.81%，平均相对误差为9.13%，最小相对误差为1.19%，均方误差为0.001 5，并且在第3 d和第4 d能够预测出其发展趋势。故该模型能够为工厂供需关系提供参考，具有现实使用意义。同时，该方法还有优化的空间，本方法只能预测短期时序，具有一定的局限性。未来可以在数据集上加入多个属性，使得重构后的相空间内容更加丰富，进而降低多步预测的误差，使得预测模型具有更高的可扩展性。