基于灰色关联法的膨胀岩崩解性影响因素分析

2020-08-06唐骁宇高文华张宗堂易梅辉

水资源与水工程学报 2020年3期

唐骁宇，高文华，张宗堂，易梅辉，邬俊

(湖南科技大学岩土工程稳定控制与健康监测湖南省重点实验室，湖南湘潭 411201)

1 研究背景

膨胀岩是一种特殊类型的软岩，且与水关系紧密，亲水性强烈[1]。膨胀岩中所含有的大量亲水矿物使其在干湿循环作用下发生不均匀的体积变化，进而产生崩解。膨胀岩在我国广泛分布，修建在膨胀岩地区的交通、水利、矿山等领域的工程遇水崩解的问题也日益突显，所以，研究分析膨胀岩的崩解特性具有重要意义。对于已有的膨胀岩的崩解性研究，国内外学者通过岩石崩解试验，证明岩石崩解现象的必要条件是湿度变化，即水分迁移[2-4]。同时，膨胀岩在多次干湿循环造成的水分迁移作用下，其崩解反应随干湿循环次数的增加而逐渐累积[4-5]。在膨胀岩的崩解过程中，由于其崩解产物的粒径分布具有良好的分形特征，使得膨胀岩的崩解性可以用分形维数来表示。

膨胀岩的崩解特性是多种因素造成的，为探究其各因素之间的关联程度，结合数据样本量稀少和影响因素信息贫乏的特点，本文采用灰色关联分析法。灰色关联分析法来自于由邓聚龙[6]创立的灰色系统理论，该方法对比因素间的动态发展趋势的异同程度，并衡量因素之间的关联度，可以有效地处理分析数据“样本量稀少和影响因素信息贫乏”的问题[7]。关于膨胀岩崩解反应中灰色关联法的应用，申培武等[8]通过灰色关联法分析圆形度的变化特征能更好地反映膨胀岩崩解的状态，刘晓明等[9]利用灰色关联法分析膨胀岩矿物成分与其崩解之间的关系，但是关于膨胀岩在崩解过程中各外界因素对膨胀岩崩解性影响的相关程度的研究鲜有报道。因此，本文基于灰色关联分析法，对膨胀岩崩解的分形特征受不同干燥温度、不同外界扰动、干湿循环次数等因素的影响程度展开研究。

2 膨胀岩崩解特性试验

对膨胀岩进行静态崩解试验，该崩解试验的步骤为：(1)对试样进行前期加工至一定质量，烘箱设置如表1所示的固定温度，使用烘箱将试样干燥至恒重，烘干时间在24 h以上，随即取出试样，使试样冷却至室温；(2)将试样放置在合适容器中，完全浸入自来水中，持续浸泡24 h以上，同时容器中自来水的水量保持相同；(3)烘箱设置如表1所示的固定温度，使用烘箱将试样干燥至恒重，烘干时间在24 h以上，随即取出试样，使试样冷却至室温，然后对试样进行筛分试验，该环节中标准筛的筛孔径为60、40、20、10、5、2、1、0.5、0.25、0.075 mm，分别称量并做好记录，其中粒径小于0.075 mm的部分通过质量守恒求得。上述(2)、(3)步骤作为一次干湿循环，由于本试验需要20次干湿循环，所以将每次干湿循环后的崩解物残留样重复上述步骤(2)、(3)，直至完成试验。

根据不同干燥温度情况下的静态崩解和动态崩解试验以及初始单块质量不同情况下的静态崩解试验，分析温度变化、初始扰动程度和干湿循环次数等影响因素对膨胀岩崩解性的关联度，其中根据相关试验测定[10]，TN01、TN02、TN03、GN01、GN02、GN03为强膨胀岩，TL01、TL02、TL03、GL01、GL02、GL03为中强膨胀岩，各试验方案分别见表1和2。

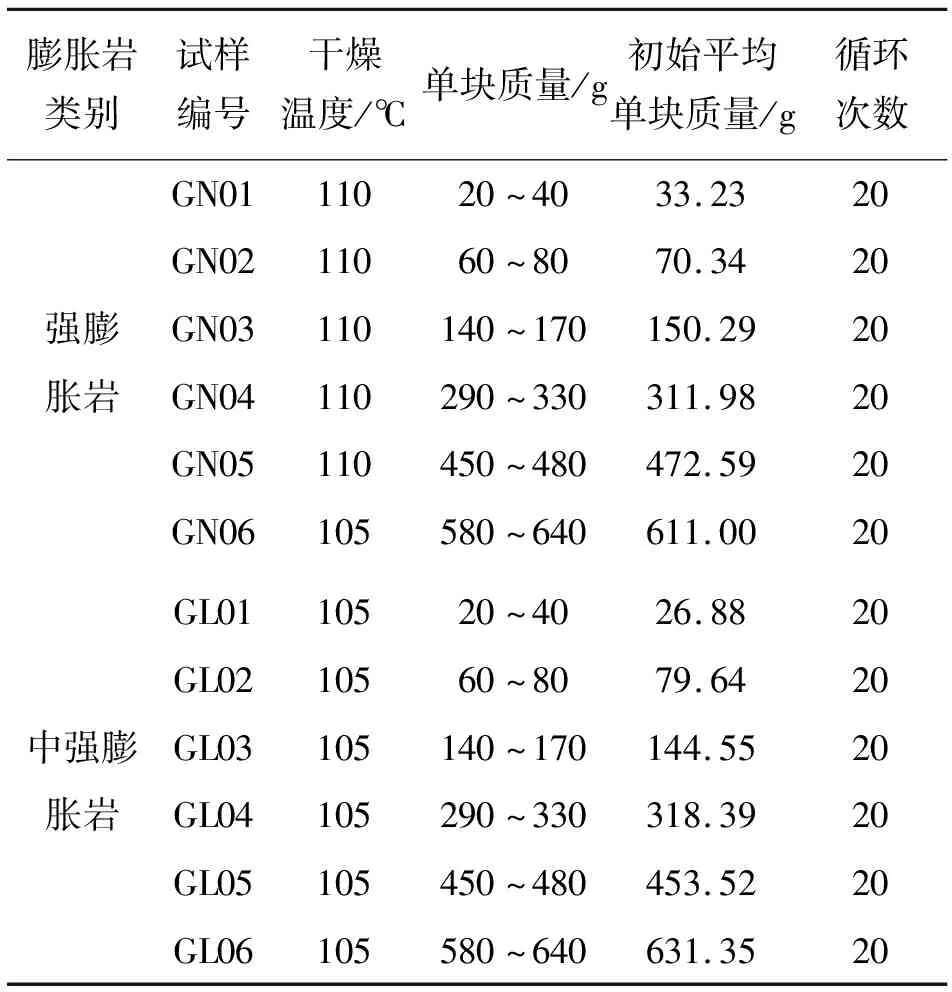
表2 不同初始单块质量试验方案表

3 膨胀岩崩解的分形特征

3.1 质量与粒径关联的分形维数计算方法

分形几何是常用来描述自然界杂乱不规则现象的手段[11]，目前多采用自相似性分形。而膨胀岩是亲水矿物颗粒胶结而成的几何体，水的作用下其崩解现象反应活跃，且膨胀岩的崩解现象是由大量微小破碎集聚成的小破碎组成。相关研究发现，膨胀岩具有从内部损伤到外部破碎的自相似性行为[12]，所以分形理论适用于分析膨胀岩的崩解反应。

由于膨胀岩的室内浸水崩解试验可以方便可靠地得到崩解后膨胀岩的各粒组颗粒分布情况，且自相似性一般是分形维数的基础，因此，本文采用关联分形维数[13]，对膨胀岩崩解分形进行描述。

结合韩培锋等[14]对堆石料崩解分形特征的描述，并基于分形理论，可将试样总质量设为M，对崩解物进行筛分，试样总质量包括该筛网下的崩解物总质量以及剩余的崩解物总质量，即：

M=Ma(d)+Mb(d)

(1)

式中：M、Ma(d)、Mb(d)分别为试样总质量、筛网下的崩解物总质量、剩余的崩解物总质量，g；d为筛孔径，mm。

定义质量和粒径的关联函数N(d)为：

(2)

膨胀岩崩解后的崩解产物是具有开放性的自组织系统，其物质构成的空间结构由粒度分布表示。设超过某粒径di的崩解产物颗粒在三维空间中占有的体积为V，则V可表述为：

V=ηV-ηV(di/λV)3-D

(3)

式中：ηV与λV分别为描述崩解产物大小、形状的系数；D为分形维数；V为体积，mm3。

根据Tyler等的假定[15-16],膨胀岩崩解产物的不同颗粒应有相同密度，所以超过某粒径的崩解产物颗粒质量有：

Mb(di)=ρηV-ρηV(di/λV)3-D

(4)

式中：Mb(di)为超过某粒径的崩解产物颗粒质量，g。

考虑di=0和di=dmax的情况，以确定公式(4)中的参数。其中，当di=0时，公式(4)中Mb(di)为崩解产物总质量M；假定崩解产物中最大颗粒粒径为dmax，即当di=dmax时，Mb(di)=0。分别代入公式(4)，则有：

M=ρηV

(5)

λV=dmax

(6)

对公式(2)～(6)进行推导，得出膨胀岩崩解物颗粒质量及粒径之间的关系式为：

(7)

两边取对数有：

(8)

D=3-k

(9)

3.2 分形维数求解

由上述分形维数D的计算方法，可求得膨胀岩崩解的分形维数，考虑同时列举各因素影响下崩解产物的分形维数求解过程所占篇幅过大，此处仅列举TL01、TL02和TL03试样在干湿循环次数为20次时，k值的线性拟合结果如图1所示，其中横坐标为粒径比对数lg(di/dmax)，纵坐标为质量比对数lg[Ma(di)/M]。

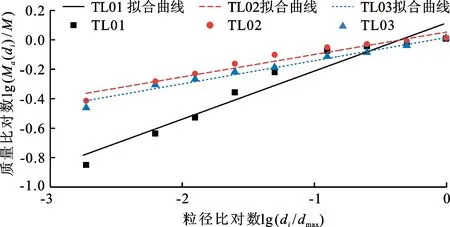
图1 TL01、TL02及TL03试样干湿循环20次k值拟合

由图1可以得出，TL01、TL02和TL03试样在干湿循环次数为20次时的相关系数R2分别为0.930、0.940、0.975，故膨胀岩崩解产物的粒径分布数据具有很好的线性拟合关系。试验数据的曲线拟合也表明，膨胀岩崩解产物的粒径分布具有分形特征。

3.3 各因素对分形维数的影响

分形维数D是膨胀岩崩解产物分形特征的量化指标，不同因素影响下，崩解产物每次经过干湿循环崩解前后的粒度分布变化的程度，表示膨胀岩颗粒发生崩解的程度。根据拟合的k值，基于影响因素为不同干燥温度和不同初始单块质量，分别得出每一次干湿循环后崩解产物的分形维数D值，并通过分形维数D值与干湿循环次数N之间的关系图给出。

图2为不同干燥温度下强膨胀岩和中强膨胀岩试样的D-N关系曲线。由图2可知，分形维数在逐次干湿循环后不断增加，其增速逐渐降低，直至平缓。根据第3.1节分形维数D的计算方式，分形维数越高，在同一粒径比对数值为横坐标的质量比对数值越小，即崩解产物中大颗粒占比相对减少、细颗粒占比相对增大。

造成上述现象的原因归结为：干湿循环造成的水分置换会定量地对膨胀岩崩解产生影响，膨胀岩在水的作用下不断在前一次干湿循环的基础上崩解，干湿循环次数越多，水分置换次数越多，膨胀岩中的亲水矿物在水分置换中不断膨胀收缩导致岩体裂隙发展，从而加剧崩解反应，导致膨胀岩岩体逐渐崩解破碎；且第2次干湿循环后，膨胀岩岩体在具有一定量初始裂隙的基础上，亲水矿物发生膨胀再收缩反应，导致较大粒径岩体颗粒迅速崩解，而随着干湿循环次数增加，小粒径崩解物颗粒质量占比不断增大，每个岩体颗粒中的裂隙影响相对降低，从而分形维数D的变化速率减小。

由图2(a)可以看出，强膨胀岩3个试样在第2次干湿循环崩解前，TN02试样的分形维数低于TN01和TN03，而在随后的崩解试验中TN02试样的分形维数增长幅度最大，而TN01试样的增长幅度最小，从而在第20次循环后，分形维数排序由小到大变为TN01、TN03、TN02。同时，从图2(b)也可看出，TL02试样的分形维数在干湿循环过程中始终高于TL01和TL03试样，TL01试样的分形维数最低。对比图2(a)与2(b)可知，强膨胀岩TN01～TN03试样崩解产物的分形维数基本高于中强膨胀岩TL01～TL03试样。

图2 强膨胀岩和中强膨胀岩试样在不同干燥温度下D-N关系图

产生以上现象的原因归结为：考虑到干燥温度是影响膨胀岩内外水分置换的重要因素之一，干燥温度作为变量的时，干燥温度为60℃的TN02、TL02试样中的含水量在每次干湿循环作用下置换时间最长，水对膨胀岩的作用效果最为明显，亲水矿物从吸水膨胀到失水收缩的体积变化程度最大，导致TN02、TL02试样崩解反应更为明显，且在每一次干湿循环后持续崩解；TN03、TL03试样相较于TN01、TL01试样在干燥过程中水分置换更彻底、水分作用时间更短，所以，相对于水分在膨胀岩内部停留的时间，亲水矿物的吸水量和失水量导致的矿物体积变化幅度能更有效地促进膨胀岩的崩解。同时，由于不同类别的膨胀岩矿物含量和组成的不同，导致强膨胀岩(TN01～TN03)的崩解反应较中强膨胀岩(TL01～TL03)更加剧烈。

良渚是现今浙江余杭县的一个地名，1936年原浙江省西湖博物馆的施昕更在这一带进行考古，发现十余处遗址，随后出版了《良渚(余杭县第二区黑陶文化遗址初步报告)》。其后，又在这一带发现同一文化类型的遗址100多处，1960年，夏鼐在《长江流域考古》一文(《考古》1960年第2期)中，正式提出“良渚文化”这一概念。

初始单块质量不仅衡量膨胀岩的初始块度大小，同时也反映了膨胀岩试样在崩解反应之前的受扰动程度。图3为不同初始单块质量的强膨胀岩和中强膨胀岩试样的D-N关系曲线。

图3 强膨胀岩和中强膨胀岩试样不同初始单块质量的D-N关系图

根据图3，在初始单块质量不同时，干湿循环次数N和分形维数D的关系曲线基本表现为：分形维数D随着干湿循环次数N的增加而不断增大，且增长速率不断减缓。膨胀岩分类为强膨胀岩时，第1次循环后，膨胀岩崩解产物的初始分形维数D按由小到大排序为GN03、GN02、GN04、GN05、GN01、GN06；第20次循环后，其分形维数D由小到大的排序为GN02、GN03、GN01、GN04、GN05、GN06。其中GN02、GN03试样分形维数D的增长幅度最大，GN01试样的增长幅度最小；GN05、GN06试样分形维数D在数值上始终较大。比较图3(a)与3(b)可知，强膨胀岩GN01～06试样崩解产物的分形维数基本高于中强膨胀岩GL01～06试样。

产生以上现象的原因归结为：在初始单块质量作为单一变量的条件下，单块质量更高的膨胀岩内部由外部作用影响导致的裂隙发展等缺陷程度更高，而质量太小的膨胀岩在加工制作土样时存在更大程度的扰动，也会在一定程度上加深对内部结构的破坏，从而导致20次循环后，初始单块质量越大分形维数越高，且单块质量低于某一值时分形维数未到达最小值；从分型维数增长幅度的方向分析，GL01、GL05、GL06试样的分形维数增长幅度低于GL02、GL03试样，是因为初始扰动比较大的试样在第1次干湿循环崩解后，其较易破碎的裂隙已经发展完毕，随后的崩解中成熟裂隙对膨胀岩崩解的影响降低所致。同样地，由于不同类别的膨胀岩矿物含量和组成不同，导致强膨胀岩崩解反应较强烈的现象，这一现象也出现在初始单块质量为单一影响因素的情况下。

4 基于灰色关联理论的膨胀岩崩解性影响因素分析

4.1 灰色关联分析法

在膨胀岩的崩解试验中，由于试验成本的限制，进行影响因素分析的试验样本数有限，而灰色关联分析法注重各种因素之间的宏观分析和基本态势等，不需要大量的数据和丰富的信息。该方法实质是分析各影响因素对被影响对象的影响程度，从中找出主要因素与次要因素。针对膨胀岩的崩解反应，不同因素对膨胀岩崩解性的影响程度各异。因此，采用灰色关联法分析膨胀岩崩解试验并进行数据分析，可以求出各因素关联度，即对膨胀岩崩解性的影响程度，从而对实际工程提出指导性意见。

灰色关联分析法在进行数据处理时，采用的是灰色关联度为特征因子对主行为序列的影响程度，该数据处理方法归纳如下[17]：

设存在一系统特征数列为参考数列(主行为)，记作Y0，其表达式为：

Y0={Y0(l)|l=1,2,…,n}

(10)

另存在一系统因素数列，记作Yi，i=1,2,…，m(m为比较数列因子个数，即点数)：

Yi={Yi(l)|l=1,2,…,n}

(11)

在膨胀岩崩解试验中，影响因素的意义各不相同，为方便对比分析，按公式(12)对参考数列(主行为)和因素数列进行无量纲化的数据变换：

(12)

i∈{0,1,2,…,m}

(13)

ΔYimax=max{|Yi(k)-Yi(l)|k,l=1,2,…,n}

(14)

(15)

式中：ξi(l)为关联系数，对应l样品在Yi对Y0中的数据；ρ为对比系数，一般为ρ∈[0,1]，本文采用0.5；Δmax为因素数列(Yi，i=1,2,…，m)在数据中各点与对应的参考数列(Y0)各点差值的最大绝对值;Δmin为因素数列(Yi，i=1,2,…，m)在数据中各点与对应的参考数列(Y0)各点差值的最小绝对值。分别按公式(16)及(17)计算：

(16)

(17)

Δi(k)为k点与参考数列对应点差值的绝对值，按公式(18)计算：

(18)

由于关联系数ξi(l)只能表示不同样品数据间的关联程度，灰色关联分析法为解决关联系数存在不易于集中对比的这一问题，将关联系数集中处理，最终结果以关联系数的平均值来表示因素间的关联程度，即灰色关联度。关联度计算公式为：

(19)

关联度ri表示因子Yi对主行为Y0的影响程度，对于l,j∈(1,2,…,n)，当Yl>Yk时，那么认为系统因素数列Yl相较于Yk与主行为数列的相关性更高。

4.2 试验结果分析

试验设置的控制影响因素包括干燥温度(30℃、60℃、105℃)、初始单块质量、干湿循环次数。对该3种影响因素进行灰色关联分析，定义膨胀岩崩解产物的分形维数D为主序列。其中干燥温度反映膨胀岩的干湿循环过程中膨胀岩含水率变化的速度和含水量变化率的大小，初始单块质量反映膨胀岩在崩解反应之前初始扰动的程度。定义序列1(Y1)为干燥温度，序列2(Y2)为初始单块质量，序列3(Y3)为干湿循环次数。

根据4.1中所述的灰色关联分析计算步骤计算得到干燥温度、初始单块质量、干湿循环循环次数与崩解产物分形维数的关联度，计算结果见表3。

表3 各影响因素对崩解产物分型维数的关联度

由灰色关联度理论得知，参考数列和各影响因素数列的关联度能反映各因素数列对参考数列的影响程度，且关联度和影响程度呈正相关。由表3可知，3个影响因素与膨胀岩崩解产物的分形维数D均有一定的关联度，关联度排序为Y3>Y1>Y2，即干湿循环次数对膨胀岩崩解产物的分形维数的影响程度最大，然后依次是干燥温度、初始单块质量。从膨胀岩崩解的机理出发，红砂岩崩解反应的关键是其矿物含量及组成情况，由于红砂岩富有大量的亲水性、可溶性和膨胀性矿物，这些矿物具有连接力弱、比表面积大等特点，使膨胀岩在干湿循环中导致岩体内含水量变化时，发生膨胀收缩的崩解现象。因干湿循环次数反映的是膨胀岩崩解过程中水分置换的定量情况，所以对于膨胀岩崩解反应的影响因素中，水分置换次数的影响最高，岩体内含水量变化程度和速度对膨胀岩体崩解的作用次之，崩解反应前膨胀岩的受扰动情况作用相对较弱。

由于膨胀岩具有遇水崩解的现象，需要膨胀岩的分形维数达到一个稳定值，而膨胀岩在自然环境中崩解的时间超出工期限制，就要对膨胀岩进行人为促进的预处理。实际操作具体为，将爆破开采的膨胀岩先进行若干次人为的干湿循环处理，使较大岩块中的初始裂隙快速发展，然后进行人工破碎，在增大岩块表面积的同时，加剧新裂隙的形成和发展；尽量在高温季节对膨胀岩作多次干湿循环的崩解处理。通过这种人为的控制使膨胀岩快速软化崩解，从而达到工程指标。