相干态辐射场的Husimi分布函数在非对易相空间中的表示

王兴忠

（宁波财经学院，浙江宁波315175）

任何算符（可展开成位置或动量算符乘方之和）的期望值，都可以利用分布函数进行计算。其中Husimi分布函数的结构较为简单，对物理意义的诠释比其他分布函数更具优势[1]。用一个压缩的高斯波包（最小不确定波包）对Wigner分布函数进行滤波可产生Husimi分布函数，此时，Wigner分布函数中的精细结构被消除，但物理上有意义的信息不会缺失[2-4]。Husimi分布函数的这种特性在研究复杂系统的量子动力学时具有特殊重要性[5-6]。

在一般混合态中，物理量算符的平均值须考虑量子力学平均和统计物理平均[7]，即

其中，ρ称为混合态的密度算符，

如取pi=δiα，即得纯态

另一方面，又可利用分布函数F(q,p,t)来计算物理量算符的平均值[8]：

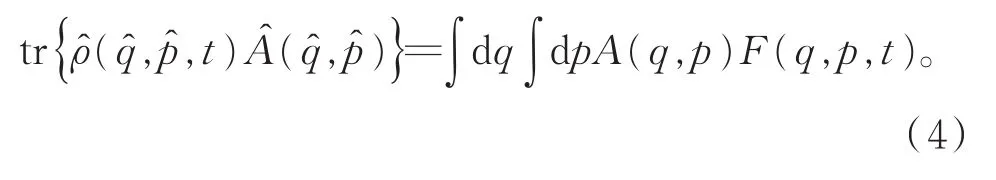
1 Husimi分布函数

真实的概率分布是非负的。用一个高斯波包对Wigner分布函数进行滤波，可得到一个非负分布，此分布通常指的就是Husimi分布函数，因此，Husimi分布函数可定义为[7]

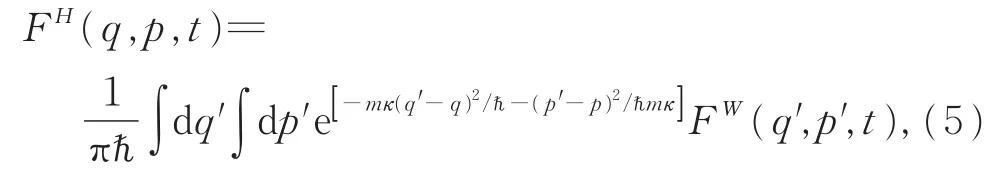
其中κ为任意正常数。若令κ等于频率ω，则Husimi分布函数转化为反常顺序的Q函数，用来描述谐振子或辐射场。当然，从基本关系式（4）出发，也可以定义Husimi分布函数。

Husimi分布函数是密度算符在压缩态表象的表现形式[9]，

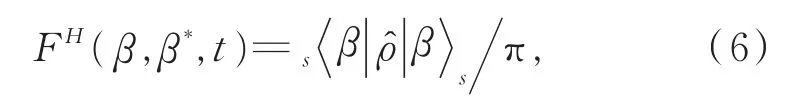
其中，

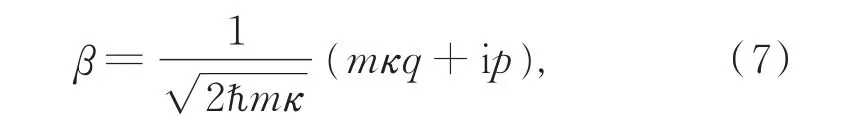
与β对应的算符

算符的本征态就是最小不确定压缩态。当κ=ω，压缩态就变成通常的相干态。

在(q,p)相空间，式（6）可表示为

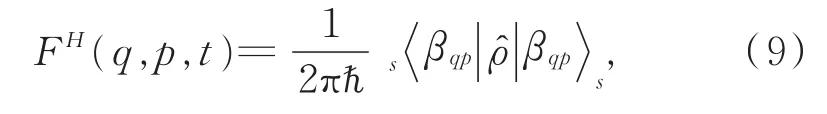
对于纯态，式（9）变为

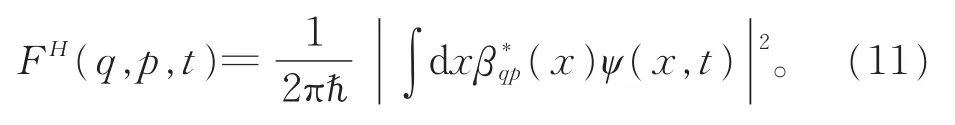
2 非对易相空间中物理量的表述

在非对易相空间中，函数的自变量是算子，可将算子作为希尔伯特空间的算符。对于由Heisenberg-Weyl代数描述的非对易相空间，有关系式[10]：

物理量在非对易相空间中可用2种方法来表述：（1）将非对易相空间中的函数看作普通函数，即其中的坐标和动量可交换，将函数之间的乘法改为Moyal星乘法。（2）将坐标和动量作为算子，即非对易相空间中的函数自变量是算子，函数本身就成了一个算子，此时，函数之间的乘积为普通乘积。

在非对易相空间中，物理量和物理方程都将发生变化[11]。利用Bopp变换[12-13]，可将非对易相空间中的算符参量用普通空间中的参量来表示，从而将普通空间中的力学量变换到非对易相空间中，使非对易相空间中的星乘法转换为普通乘法。

3 普通空间中的辐射场

相干态、真空态和压缩态均满足Heisenberg不等式的下限，为最小不确定态。区别在于相干态与真空态各向不确定性均相等，其中真空态平均强度为零，相干态平均强度不为零。而压缩态各向不确定性不同，被压缩的方向不确定性减小，与其正交的方向不确定性放大[14-15]。

在相干态中的辐射场等效于最小不确定高斯波包，此波包的中心点在q0，宽度Δq=并随平均动量p0在简谐势中运动。其波函数为

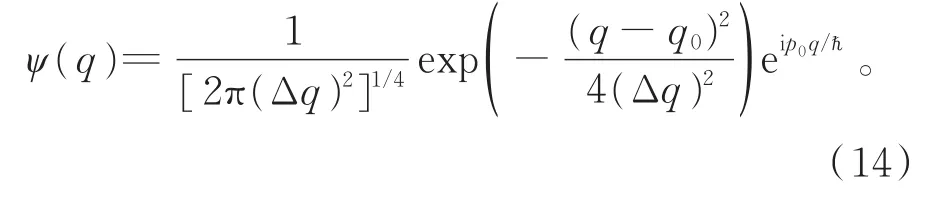
其Wigner分布函数为[16]

由式（5）对式（15）进行高斯滤波，即得到高斯波包的Husimi分布函数[17]

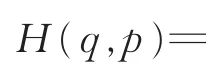
对于辐射场，取m=1，κ=ω，有

在相干态中的辐射场，满足最小不确定条件:

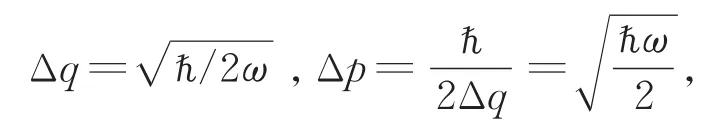
得

将式（16）或（18）与式（15）进行比较，可知一个高斯分布的高斯滤波在q和p空间产生了都变宽的高斯分布。

对式（18）进行进一步推广，得到三维普通空间中相干态辐射场的Husimi分布函数

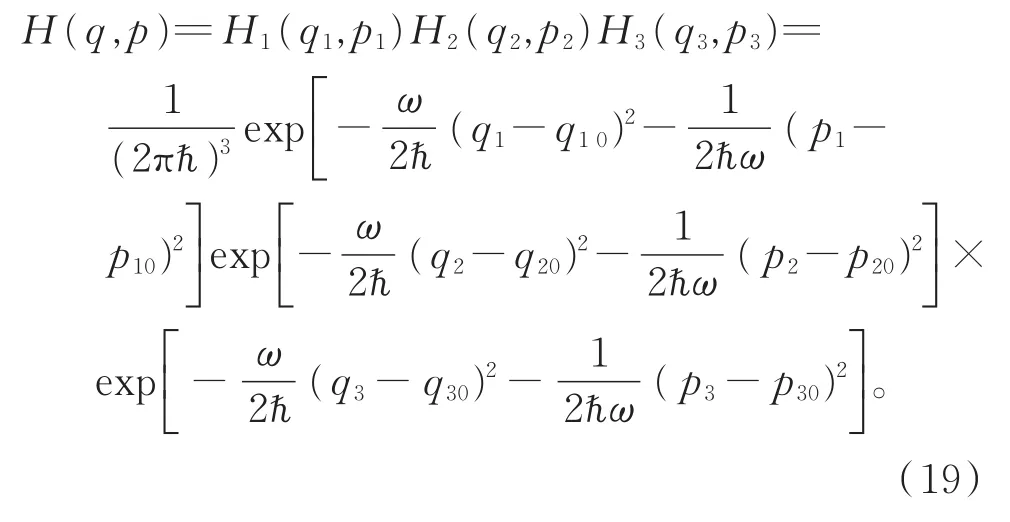
4 非对易相空间中的相干态辐射场的Husimi分布函数

将普通对易空间中的三维相干态辐射场Husimi分布函数式（19）进一步推广到三维非对易相空间。以非对易相空间中的自变量为算子，即作代换

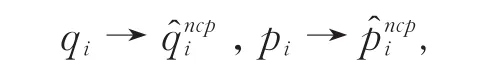
有

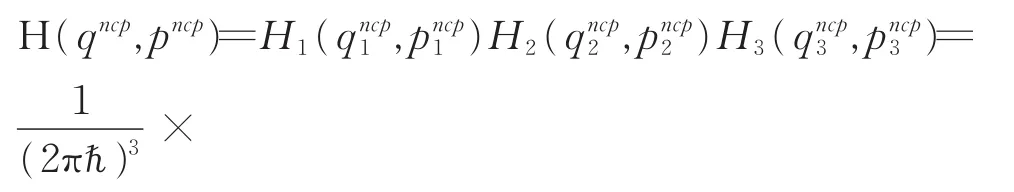
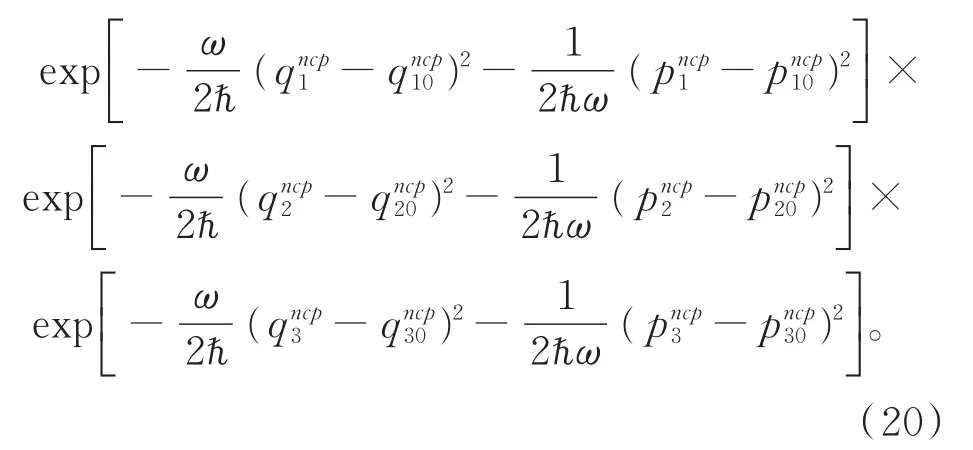
利用Bopp变换:

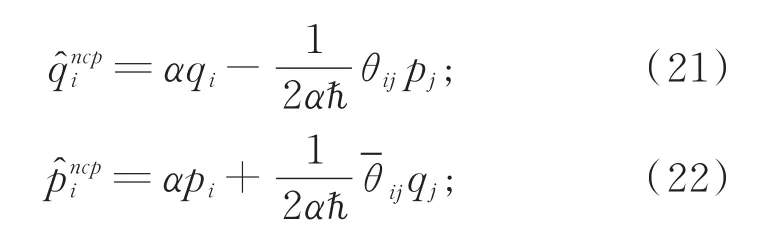
其中，θij和ij为完全反对称矩阵，α为对称矩阵。

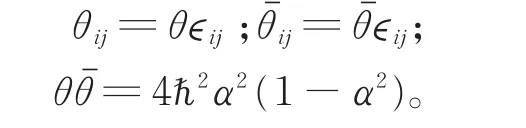
取完全反对称矩阵∈为

最后就得到非对易相空间中的三维相干态辐射场的Husimi分布函数用对易空间中的参数来表示时的表达式：

5 讨 论

对照式（19）与（24）可以发现，在经典的对易空间中，由于坐标与坐标、动量与动量之间是对易的，所以三维相干态辐射场的Husimi分布函数的各个维度是独立的，没有出现各维度参数互相影响的情况。而在非对易相空间中，由于坐标与坐标、动量与动量之间不再对易，此时，各个维度的参数就有了联系，而联系的强度取决于辐射场的能量（θ值的大小），每个维度的情况与其他2个维度的参数有关，为3个维度参数的函数。

Husimi分布函数是Q函数的一般形式，具有非负性，适合描述系统的概率分布。此函数通过对Wigner分布函数进行高斯滤波得到。通过高斯滤波，可除去原函数中的精细部分，不影响对物理性质的描述。所以在复杂系统的表述中，Husimi分布函数具有一定优势。相干态辐射场是物理系统的基本组成单元，是研究复杂系统的基本出发点，所以，在研究非对易相空间中的物理现象时，对辐射场的研究至关重要的，而Husimi分布函数是其最基本的表述之一。因此，对非对易相空间中的相干态辐射场的Husimi分布函数进行研究具有基础性意义。