基于改进灰色模型的石河子市需水量预测

吴 凡，陈伏龙，张志君，龙爱华,2，何新林

(1.石河子大学 水利建筑工程学院，新疆 石河子 832000；2.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038)

1 研究背景

西北内陆区水资源短缺，伴随着城市经济社会的不断发展，新型工业化、信息化、城镇化和农业现代化的快速推进，用水量急剧上升，水资源供需矛盾日趋尖锐，对水资源进行优化配置是解决供需矛盾的关键[1]，而需水量的科学预测是优化配置的基础环节之一，也是城市水资源规划与管理的重要内容之一。

居民生活、第一产业、第二产业、第三产业和生态环境用水构成了需水预测的主要部分[2]。现有需水预测方法依其对数据处理方式的不同可分为人工神经网络、随机森林模型、灰色预测方法以及系统动力学方法等[3-6]。灰色预测模型适合处理诸如需水量预测的贫信息系统，并且简单实用，原理容易理解且预测结果较精确[7]，因而得到了广泛的采用。汪妮等[8]通过建立新陈代谢灰色预测模型，对宝鸡市工业需水量进行预测。赵桂生等[9]基于我国2005-2014年间的农业用水数据，构建了新陈代谢灰色模型，并与原始模型进行对比，发现改进后模型精确性提高。王有娟等[10]针对传统灰色预测模型存在的不足，建立了二次修正后的灰色组合模型，对浙江省工业用水进行了预测。苗志刚等[11]建立了灰色支持向量机的城市需水量预测模型，得到的结果表明预测误差小于单一的支持向量机和灰色模型。城市需水量受到经济发展、人口变化、三产业占比、居民生活品质等条件的影响，原始序列呈现出一定的波动性，导致预测的准确性失真。为解决此问题，刘思峰等[12]提出了缓冲算子理论，其作用是强化原始数据的大致趋势，能有效地降低外界因素对预测模型的影响。刘松等[13]通过将同性缓冲算子进行组合，得出一种新的缓冲算子，实例证明其能提高模型的预测精度和扩大算子的适用范围。程欢等[14]在原有灰色GM(1,1)模型的基础上引入二阶弱化缓冲算子，对成都市未来15年的需水量进行了预测研究。杜懿等[15]对传统灰色GM(1,1)模型进行了不同程度的改进，并以广西省为例对需水量进行了预测，结果表明经两阶段弱化算子处理后生成的原始序列，代入模型后较其他模型预测精度高。

虽然引入缓冲算子能够有效地提高原始序列的光滑度及模型的精度，但同时也存在一些问题：在面对一些实际问题时，一阶弱化缓冲算子有时会表现出作用强度不够，而二阶弱化缓冲算子的作用强度又太大[16]，会对后续的预测精度造成一定影响，因此，弱化缓冲算子作用强度的控制决策成为了原始序列预处理的关键。为解决以上问题，本文在建模过程中引入变权弱化缓冲算子，结合实际情况融入预测人员的定性分析，确定带权重的缓冲算子，实现对弱化缓冲算子作用强度的控制，建立含有变权弱化缓冲算子的新陈代谢GM(1,1)模型，以期提高预测模型的精度。

本文基于石河子市用水资料，采用改进的灰色预测模型和定额法(指标分析法)预测石河子市需水量。并将两种方法预测成果进行比对分析，其结论可为区域水资源优化配置提供科学的理论依据。

2 研究区概况

新疆维吾尔自治区石河子市位于北疆地区石河子垦区中部，天山北麓中段，准噶尔盆地南部，面积约460 km2，东距自治区首府乌鲁木齐155 km，西距边陲重镇霍尔果斯口岸460 km。由南向北依次为天山山区、山前丘陵区、山前倾斜平原、洪水冲积平原、风成沙漠区，平均海拔高度450.8 m。研究区地表水资源主要为泉水、河水。过境共有宁家河、玛纳斯河等5条河流，区域内河流多年平均径流量为12.23×108m3，垦区多年地下水平均资源量为5.87×108m3，地下水可开采量为3.92×108m3。2018年石河子市经济社会用水总量占水资源总量的78%，远远超过了国际上公认的任何一个区域“水资源开发利用率都不应超过40%”的标准。

3 预测方法

3.1 新陈代谢灰色预测模型的建立

3.1.1 原始GM(1,1)模型建立 1982年，灰色系统理论由著名专家学者邓聚龙[17]首创。建模过程如下：

(1)GM(1,1)灰色模型建立。假设X(0)为初始序列，X(0)=((X(0)(1),X(0)(2),…,X(0)(n))，记X(1)=AGOX(0)为一次累加序列，则有X(1)=((X(1)(1),X(1)(2),…，X(1)(n))。

对X(1)建立单变量的一阶微分方程GM(1,1)模型：

(1)

式中:a、b为待辨识参数。

对方程式(1)做离散化处理,得到新生成的白化方程式：

x(0)(m)-az(m)=b(m=2,3,…,n)

(2)

应用最小二乘法，从方程式(2)可求得辨识参数a、b的估值为：

(3)

(4)

式中：Z=(z(2),z(3)，…，z(n))为X(1)的一次均值生成。

公式(4)与下式等价：

B=(ATA)-1ATYn

(5)

其中：

式中：AT为矩阵A的转置，(ATA)通常情况下为满秩矩阵，因此其逆(ATA)-1存在。

对X(1)实行累减还原，得到x(0)(m+1)的预测值为：

(6)

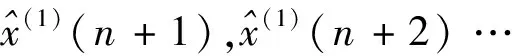
(2)模型的检验。建立的GM(1,1)模型预测结果与实际序列将存在一定偏差，模型必须满足精度要求才有较强的可信度。评价模型精度的主要方法分为相对误差检验法和后验差比检验法。精度检验参照表见表1。

表1 模型精度检验参照表

3.1.2 新陈代谢GM(1,1)预测模型 由于灰色模型短期预测精度高，随着时间的增长精度将逐渐降低。为了规避这个缺点，将递推法引入灰色模型。根据等维递补原理，将通过模型预测所得的新数据加入初始数据序列X(0)=(X(0)(1)，X(0)(2)，…，X(0)(n))中，并同时将最久远数据X(0)(1)、X(0)(2)剔除。初始序列变为X(0)=(X(0)(3),X(0)(4),X(0)(5),…,X(0)(n+1),X(0)(n+2))，反复操作，根据数列顺序依次递补，从而建立新陈代谢GM(1,1)模型，直到预测结果达到所需年份，预测完成。

3.2 含有变权缓冲算子的新陈代谢GM(1,1)预测模型

X(0)D1=(X(0)(1)d1，X(0)(2)d1，…,X(0)(n)d1)

(7)

其中X(0)(k)d1=λX(0)(n)+(1-λ)X(0)(k)

式中：λ为可变权重，0<λ<1，k=1,2,3,…,n；当初始序列X(0)呈单调增长趋势、单调递减趋势或震荡趋势时，D1称为弱化缓冲算子，并称D1为变权弱化缓冲算子。

3.2.2 变权弱化缓冲算子的作用强度 设X(0)=(X(0)(1)，X(0)(2)，…,X(0)(n))为非负的初始用水数据序列，初始数据序列X(0)中X(0)(k)到X(0)(n)的平均变化速率称作r(k);D1为作用于X(0)的变权弱化缓冲算子，X(0)经变权弱化缓冲算子D1作用后所得到新的数据序列为X(0)D1=(X(0)(1)d1,X(0)(2)d1,…,X(0)(n)d1)，则将

(8)

称作变权弱化缓冲算子D1在k点的调节度。

调节度可定义为变权弱化缓冲算子对原始用水数据序列的作用强度，而变权弱化缓冲算子可通过改变其权重λ的取值，从而对原始序列施加不同程度的影响。

由于

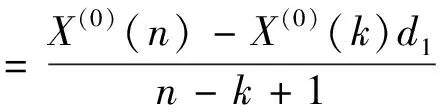
在枪声定位系统中，传感器节点的主要工作包括声信号的采集与分析、无线数据通信、数据融合等，节点需要实现的功能复杂且任务繁重。系统中采用FPGA作为核心逻辑处理器，实现节点的多任务并行处理[8]，为系统的实时性要求提供硬件支持。节点的硬件可以分为声信号传感模块、逻辑控制模块、无线通信模块、OLED显示模块、GPS定位模块、姿态传感器和电源模块等主要模块，如图5所示。

=(1-λ)r(k)

(9)

所以

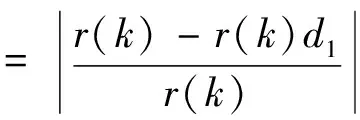
(10)

式中：λ为可变权重，0<λ<1；k=1,2,…,n。变权弱化缓冲算子D1在各点的调节度取值范围为0<δ1(k)<1。

3.2.3 可变权重的确定 变权弱化缓冲算子对原始序列作用强度δ可用具体数学表达式描述，可变权重λ为连接预测模型与作用强度δ之间的桥梁。因此，精准地确定可变权重λ对于原始序列的预处理及提高模型精度是尤为重要的。研究人员可通过专家打分法或试算法估计出多个可变权重λ。将各个可变权重依次代入模型中，得出预测结果，并与实际值对比，取相对误差最小的λ作为该原始序列对应的变权缓冲算子的权重。

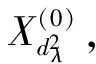
3.3 指标分析法

指标分析法又称定额法，定额的制定来源于历年研究区域用水数据，主要依据常住居民人口(或国民生产总值)，对未来需水量进行预测[18]。本文所用的各项用水定额来自于石河子市城市总体规划、新疆维吾尔自治区用水定额等报告。指标分析法从居民生活用水、第一产业用水、第二产业用水、建筑业及第三产业用水、生态用水5个方面进行需水预测。

4 实例分析

4.1 模型验证

4.1.1 数据来源 本文选取新疆石河子市作为研究区域，用水资料来源于《石河子市水资源公报(2011-2018年)》[19]《石河子统计年鉴(2011-2018年))》[20]等统计资料。具体数据见表2。

表2 2011-2018年石河子市年用水量 108 m3

4.1.2 模型精度比较 基于石河子市2011-2016年用水数据，拟用传统的GM(1,1)模型直接进行用水量预测；一阶弱化缓冲算子、二阶弱化缓冲算子、变权弱化缓冲算子分别作用后再进行预测，从而得出2017-2018年的石河子市的用水量预测值，并与实际值进行对比分析，从而体现变权弱化缓冲算子较一、二阶弱化缓冲算子的优越性。

(1)传统GM(1,1)模型预测结果。未经数据预处理过程，将原始序列直接代入传统GM(1, 1)模型进行预测，结果见表3。

表3 2017-2018年石河子市用水量传统 GM(1,1)模型预测结果

(2)通过文献[12]中提出的构建一、二阶弱化缓冲算子的方法对原始序列进行预处理。

令：

其中：

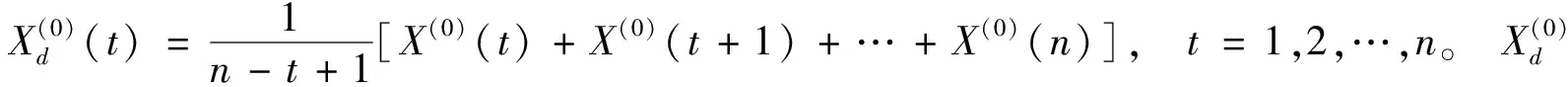
令：

其中：

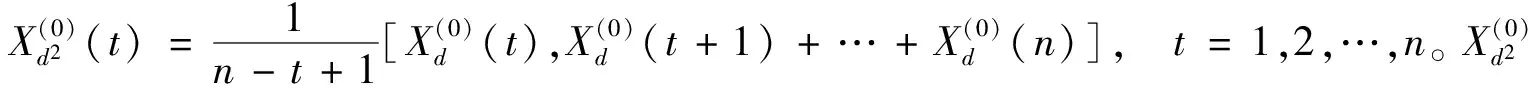
对原始序列一阶缓冲算子后，则有：

对原始序列二阶缓冲算子后，则有:

将经过一、二阶缓冲算子处理后的序列代入模型进行预测，结果见表4。

由表4可知，原始序列分别经过一、二阶弱化缓冲算子处理后得出的预测值与实际值的平均相对误差为-5.14%和5.76%，较平均相对误差为7.38%的传统GM(1,1)模型预测精度略有提升。但对照表1给出的模型精度值，均未满足一级精度标准。由此可见，无论是一阶弱化缓冲算子还是二阶弱化缓冲算子，所得到的预测结果仍存在误差稍大的情况。原因在于，以上两种弱化缓冲算子均不能实现对原始数列进行适当的调整，从而导致弱化作用效果或强或弱。

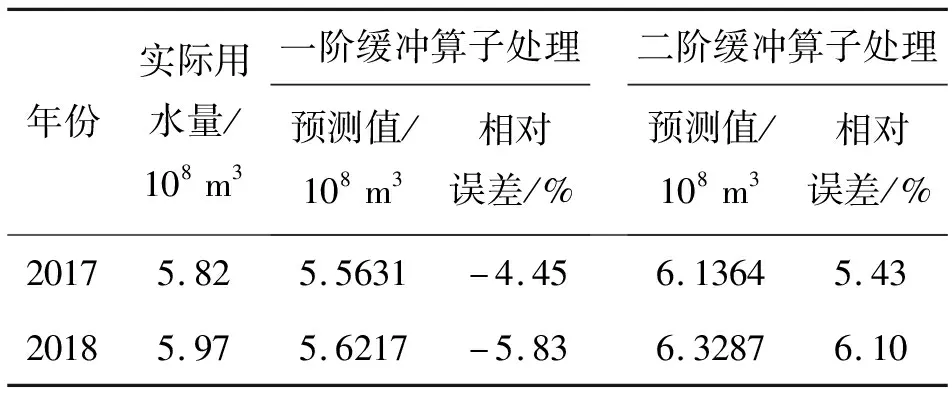
表4 2017-2018年石河子市用水量经一、二阶缓冲算子作用后预测结果

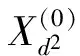
当λ=0.7时：

当λ=0.8时：

当λ=0.9时：

将3种λ取值得出的新序列代入模型进行预测，结果见表5。

由表5可知，原始序列经过变权弱化缓冲算子处理后，模型预测精度进一步提高。序列经3种不同取值下的λ处理后预测得出的结果相对误差均小于3%，满足一级精度标准。其中当λ=0.8时，预测值与实际值的平均相对误差仅为1.20%，效果最佳。实现了将预测人员的定性分析引入预测过程，从而确定最佳的权重取值。

表5 2017-2018年石河子市用水量可变权重不同取值下的预测结果

4.2 基于改进灰色模型的需水量预测

为了进一步检验模型的改进对长期预测结果准确性的影响，以及模型运行过程随时间推移对预测稳定性的影响，表6给出了石河子市2011-2018、2013-2020、2015-2022和2017-2024年经变权弱化缓冲算子处理后的用水量值、经新陈代谢GM(1,1)模型预测得出的结果及后验差比值。

根据表6可知，后验差比平均值为0.0575，最大值为0.08417，最小值为0.03511。结合表1给出的后验差比值检验模型的精度，后验差比均小于0.35，改进后模型级别为一级，证明经变权弱化缓冲算子处理后的序列代入模型运行后预测精度高。各年份时段后验差比之间浮动不大，模型稳定性较好。为了更直观地展示改进模型的预测可靠性，将算子处理后的用水量值与预测需水曲线进行拟合，石河子市不同年份时段拟合结果如图1所示。

表6 石河子市不同年份时段检验改进模型准确性及稳定性结果

由图1(a)～1(d)可知，经算子处理后的用水量呈逐年增加趋势，预测需水量点据均匀地分布在经算子处理后的用水量曲线的周围，用水量曲线与需水量曲线拟合度高，说明模型预测效果较好。可以用来进一步预测石河子市2025及2030年的需水量，预测结果见表7。

图1 石河子市不同年份时段经算子处理后的用水量及预测需水量拟合结果

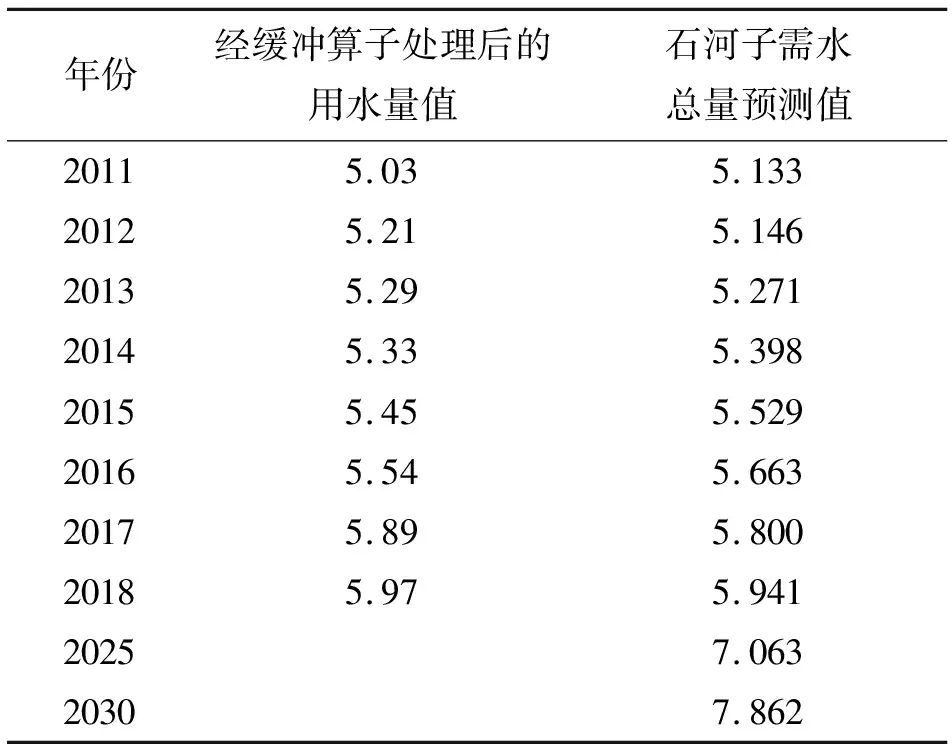
表7 石河子市不同年份改进灰色模型需水量预测结果 108 m3

从用水资料来看，2011-2018年石河子市实际用水量总体呈现快速上涨态势，但上涨过程中也有下降，原始序列呈现一定的波动性，为了弥补预测模型对波动性数据预测的缺陷，引入缓冲算子，通过其减弱序列波动性、极端值对预测模型精度的影响，强化序列的大致趋势，将原始序列尽可能处理成符合指数变化规律的新序列，从而提高预测过程的准确性。本文通过变权弱化缓冲算子处理，将原始序列重新生成为光滑、趋势明显的新序列，由新序列进行预测得出的结果上升趋势亦明显。

4.3 指标分析法

居民生活、第一产业、第二产业、第三产业和生态环境用水构成了需水预测的主要部分。生活需水量主要包括城镇居民和农村生活用水；第一产业中主要包括农业、渔业和牲畜用水；第二产业用水主要包括工业用水；第三产业用水主要是建筑业、交通运输业、服务业、批发零售、金融业和社会组织教育等；生态环境用水主要体现在河道外生态环境用水。2025和2030年石河子市生活、三产、生态环境需水量预测总表见表8。

表8 2025和2030年石河子市生活、三产、生态环境需水量及需水总量预测表 104 m3

由表8可知2025年至2030年间，第二产业用水量增加迅速，原因是在新疆生产建设兵团“十四五”规划下，石河子市在此期间大力发展工业，使得工业用水量大幅度上升，将导致水量供需缺口增大。建议石河子市在未来采用以供定需的水资源分配模式，以目标效益最优倒逼产业进行转型升级，同时大力研发引进工业节水设施技术，从而达到合理抑制用水需求的目的。

4.4 预测结果对比分析

将石河子市2025和2030年通过改进灰色模型预测所得的需水总量与指标分析法预测结果进行对比，见表9。

表9 模型预测结果对比分析表

指标分析法所用的各项经济社会发展指标及其相关用水定额均来自于已有的相关研究成果：《石河子市城市总体规划》、《新疆维吾尔自治区用水定额》等，其预测过程可信度较高，结果符合实际；由上表可知，改进灰色模型与指标分析法预测结果相近，平均相对误差仅为0.7%，佐证了改进的灰色预测模型随着时间推移仍能保持其稳定性和准确性。

5 结 论

(1)本文通过建立含有变权弱化缓冲算子的GM(1,1)模型与传统GM(1,1)模型、经一阶弱化缓冲算子、二阶弱化缓冲算子作用后的模型进行预测，并将结果进行比对分析。结果表明变权弱化缓冲算子实现了将预测人员的定性分析引入预测过程，从而确定原始序列所对应的最佳权重。将算子作用后生成的新序列代入新陈代谢GM(1,1)模型，预测结果显示后验差比值均较小，通过改进灰色模型与指标法分析法预测结果进行对比，印证了随着时间的推移模型依然能维持其稳定性和预测精度。

(2)由改进灰色模型需水预测结果可知，区域需水量变化趋势为逐年增加。石河子市的社会经济发展状况决定了未来较长时间内需水量仍将呈上升趋势。因此，优化产业结构、挖掘节水空间、提高用水效率势在必行，故下一步的工作是基于本次预测结果对石河子水资源提出区域水资源系统协调优化配置的最佳供水用水方案及适应性对策。