具有一般奇异项的Kirchhoff型方程解的研究

王佳钰， 郑晓霞， 韩 伟， 姚江燕

(中北大学 理学院， 山西 太原 030051)

0 引言及结论

本文考虑如下Kirchhoff型方程

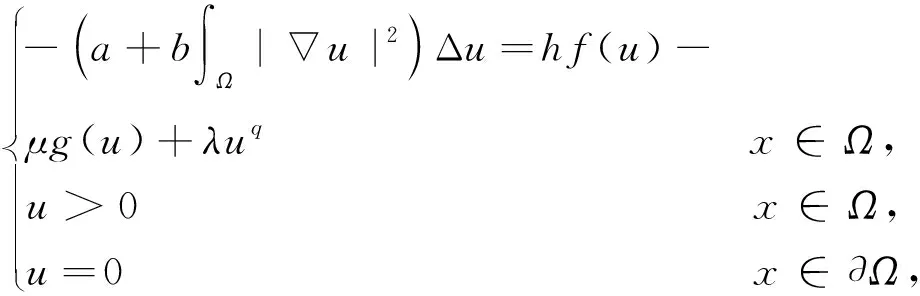
(1)

式中：Ω⊂RN(N≥3)为一个具有光滑边界∂Ω的有界区域，a,b≥0且a+b>0,λ,μ∈[0,+∞],q∈(0,3).g(u),h(x)与f(u)满足如下假设条件：

(h)h∈L2*/(2*-1-γ)， 满足h(x)>0，a.e.x∈Ω；

(g)g∈C(R+,R+)并且存在c>0， 使得g(s)≤c(s+s2*-1)，s∈R+.

(2)

(3)

c4(‖u‖2+‖u‖2*),

(4)

接下来定义问题(1)所对应的能量泛函

(5)

(6)

近年来， 许多学者针对基尔霍夫问题解的性态进行了研究[1-9].

文献[6]研究了奇异基尔霍夫型问题， 通过极大极小值方法， 得到了解的存在性与唯一性结果. 文献[5]研究了如下的Kirchhoff方程

并采用极大极小值方法， 得到了正解的存在性. 文献[10]通过变分方法得到了具有一般奇异项的Kirchhoff-Schrodinger泊松系统正解的存在性和唯一性.

受到上述文献的启发， 本文考虑问题(1)解的性态， 文献[5]只考虑了三维的情形， 而本文的结果推广到了N≥3的情形.

本文的结论如下：

定理1若a,b≥0，a+b>0,q∈(0,3)， 并且假设条件(f), (h)和(g)成立， 那么对任意的λ,μ∈R+， 问题(1)有一个正解且该解为I的一个全局极小值.

1 引 理

为了证明本文的主要结果， 需要如下引理.

‖h‖2*/(2*-1-γ)-c1‖h‖1-c5‖u‖1+q.

(7)

因为1-α∈(0,1),q∈(0,3)且h(x)>0,a.e.x∈Ω， 从而当t>0且足够小时， 可得I(tφ)<0， 也就是说m<0.

由h∈L2*/(2*-1-γ)(Ω)， 可知

(9)

根据Fatou引理， 可得

(10)

因此， 由范数的弱下半连续性和式(8)～式(10)， 可得

I(u0)≥m,

即I(u0)=m.

2 定理1的证明

令t→0+， 可得

因此， 由Fatou引理和引理2， 可得

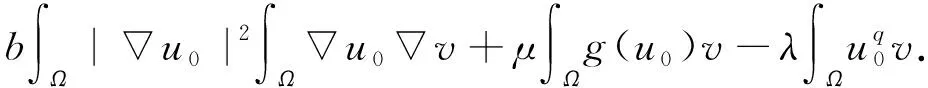
(11)

接下来证明u0确为问题(1)的一个解， 即u0满足式(6)，

(12)

定义函数Ψ∶R→R，Ψ(t)=I(u0+tu0), 即

由上面的讨论可知，Ψ(t)在t=0时达到极小值. 根据引理3， 可知Ψ(t)在t=0处可微， 且ψ(0)=0， 即

(13)

Ω+={x∈Ω∶u0+εv>0},

Ω-={x∈Ω∶u0+εv<0}，

上式表明

(14)

(15)