图的电阻距离和基尔霍夫指标综述
2021-12-23葛春雨刘家保
葛春雨,刘家保
(1.兰州交通大学 数理学院,甘肃 兰州 730070;2.安徽建筑大学 数理学院,安徽 合肥 230601)
0 引言
设图G=(V(G),E(G))为n(n≥2)个顶点m条边的连通图, 顶点度序列Δ=d1≥d2≥…≥dn=δ>0, 其中di=dvi.图G的拉普拉斯矩阵L(G)=D(G)-A(G), 其特征值μ1≥μ2≥…≥μn-1>μn=0, 其中D(G)和A(G)分别是图G的对角矩阵和邻接矩阵. 若图G中每个顶点的度相等, 则称G是正则图;若图G中所有顶点的度均为r, 则称G为r-正则图, 记作Γr.
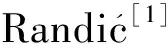
基尔霍夫指标, 记作Kf(G), 也被称为全有效电阻[2]或有效图电阻[3]. 它定义为图G中所有顶点对的电阻距离之和, 即
图的基尔霍夫指标是一个与图的拉普拉斯特征值密切相关的图的拓扑不变量. 1996年, Gutman等[4]和Klein等[5]证明了连通图G的基尔霍夫指标也可以表示为:
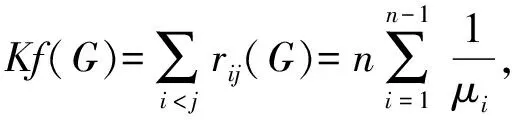
其中μ1≥μ2≥…≥μn-1>μn=0为图G的拉普拉斯矩阵的特征值.
近几十年来, 对更多图形的电阻距离和基尔霍夫指标的研究越来越多, 如距离正则图、 Fullerene图、 树图、 加权图、 轮图和扇形图、 Cayley图等. 特别地, 杨玉军和Klein[6]在2013年给出了电阻距离的递推公式以及该公式的应用.
随着研究的深入, 结合顶点的度, 又进一步衍生出度-基尔霍夫指标. 2007年, 陈海燕和张福基[7]定义了乘法度-基尔霍夫指标:

其中di(dj)表示第i(j)个顶点的度.
2012年, Gutman等[8]定义了加法度-基尔霍夫指标:
2011年, 文献[9]定义了图G的超-基尔霍夫指标:
图G的线图记作l(G), 是指以图G的边集为顶点集,l(G)的两个顶点相邻当且仅当对应的G的两条边在G中相邻. 图G的三角剖分记作T(G), 是将G的每条边uv变换成一个三角形uwv, 其中w是与uv相关联的新顶点.
下面给出图的一些运算的定义.
定义1设图G为n(n≥2)个顶点和m条边的连通图, 则S(G),Q(G),R(G),t(G)定义分别如下:
1)剖分图S(G)是将图G的每条边替换为一条长度为2的路所构成的图;
2)Q-图Q(G)是通过在图G的每条边上引入一个新的顶点, 然后通过G将相邻边上的新顶点对应连接起来而形成的图;
3)R-图R(G)是通过在图G的每条边上放置一个与之相关的新顶点, 然后将每个新顶点连接到相应边的末端顶点来构造的图;
4)全图t(G)是顶点对应于图G的顶点集和边集并集, 且t(G)的两个顶点相邻, 当且仅当对应的元素在G中相邻或关联.
定义2设G1和G2是两个图且V(G1)={u1,u2, …,u|V(G1)|},V(G2)={v1,v2, …,v|V(G2)|}, 则
1)图G1和G2的联图G1+G2:
V(G1+G2)=V(G1)∪V(G2);
E(G1+G2)=E(G1)∪E(G2)∪{(u1,u2)|u1∈V(G1),u2∈V(G2)}.
2)图G1和G2的冠图G1∘G2:取一个G1的拷贝和|V(G1)|个G2的拷贝, 然后将G1的第i个顶点和第i个G2的拷贝的所有顶点都相连,i=1, 2, …,|V(G1)|.
1 一些运算图的电阻距离和基尔霍夫指标
图运算已经被广泛地应用于分析从现实世界中抽象出来的具有拓扑性质的复杂网络. 其中字典积、 笛卡尔积、 联图、 冠图和星图等, 这些运算图的其他拓扑指标已有结果, 这里给出一些运算图的电阻距离和基尔霍夫指数.
2012年, 高兴等[10]给出了正则图的线图l(G)、 剖分图S(G)和全图t(G)的基尔霍夫指标的公式并刻画了下界成立的极图.
定理1.1[10]设G是一个连通的d-正则图, 具有n(n≥2)个顶点, 则
推论1.1[10]设G是一个连通的d-正则图, 具有n(n≥2)个顶点, 则
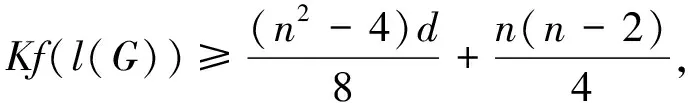
等式成立当且仅当G=Kn.
定理1.2[10]设G是一个连通的d-正则图, 具有n(n≥2)个顶点, 则
推论1.2[10]设G是一个连通的d-正则图, 具有n(n≥2)个顶点, 则
等式成立当且仅当G=Kn.
定理1.3[10]设G是一个连通的d-正则图, 具有n(n≥2)个顶点, 则
推论1.3[10]设G是一个连通的d-正则图, 具有n(n≥2)个顶点, 则

等式成立当且仅当G=Kn.
2013年, You等[11]修正了高兴等[10]在2012年求出的正则图的全图的基尔霍夫公式及其下界.
定理1.4[11]设G是一个连通的d-正则图, 具有n(n≥2)个顶点, 则
推论1.4[11]设G是一个连通的d-正则图, 具有n(n≥2)个顶点, 则
2013年, 王维忠等[12]刻画了正则图的Q(R)-图的基尔霍夫指标的公式和下界.
定理1.5[12]设G是一个n阶的连通r-正则图(r≠2), 则
推论1.5[12]设G是一个n阶的连通r-正则图(r≠2), 则

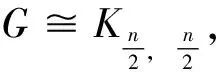
定理1.6[12]设G是一个n阶的连通r-正则图, 则
推论1.6[12]设G是一个n阶的连通r-正则图, 则
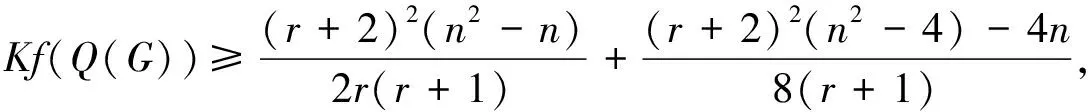
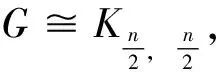
2014年, 杨玉军[13]计算了正则分子图的一些xyz变换的Kirchhoff指标, 其在文献[14]中证明了一般图的剖分图S(G)的基尔霍夫指标可以用图G的基尔霍夫指标、 乘法度-基尔霍夫指标、 加法度-基尔霍夫指标、 顶点数n、 边数m表示. 这个结果推广了高兴等[10]关于正则图的剖分图S(G)的基尔霍夫指标的结果.
2015年, Sun等[15]给出了一般图的剖分图的电阻距离和基尔霍夫指标的另一种计算公式.
定理1.7[13]设图G为n个顶点和m条边的r-正则图(r≥2), 则
定理1.8[13]设图G为n个顶点和m条边的r-正则图(r≥2), 则
定理1.9[13]设图G为n个顶点和m条边的r-正则图(r≥2), 则
定理1.10[13]设图G为n个顶点和m条边的r-正则图(r≥2), 则
定理1.11[13]设图G为n个顶点和m条边的r-正则图(r≥2), 则
定理1.12[14]设G是一个连通图, 具有n(n≥2)个顶点和m条边, 则
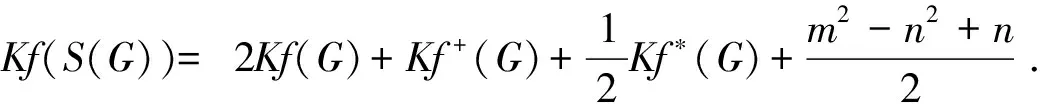
2015年, 杨玉军和Klein[16]得到了剖分和三角剖分图的加法度(乘法度)-基尔霍夫指标公式, 以及一个新的三角剖分基尔霍夫指标公式, 并给出了图的迭代剖分和三角剖分的(加法度-、 乘法度-)基尔霍夫指标公式.
定理1.13[16]设图G为n(n≥2)个顶点和m条边的连通图, 则剖分图S(G)的加法度-基尔霍夫指标为:
Kf+(S(G))=4Kf+(G)+4Kf*(G)+(m+n)(m-n+1)+2m(m-n).
定理1.14[16]设图G为n(n≥2)个顶点和m条边的连通图, 则剖分图S(G)的乘法度-基尔霍夫指标为:
Kf*(S(G))=8Kf*(G)+2m(2m-2n+1).
定理1.15[16]设图G为n(n≥2)个顶点和m条边的连通图, 则迭代剖分图Sk(G)的乘法度-基尔霍夫指标为:
定理1.16[16]设图G为n(n≥2)个顶点和m条边的连通图, 则迭代剖分图Sk(G)的加法度-基尔霍夫指标为:
定理1.17[16]设图G为n(n≥2)个顶点和m条边的连通图, 则迭代剖分图Sk(G)的基尔霍夫指标为:

(m-n+1).
定理1.18[16]设图G为n(n≥2)个顶点和m条边的连通图, 则三角剖分图T(G)的基尔霍夫指标为:
定理1.19[16]设图G为n(n≥2)个顶点和m条边的连通图, 则三角剖分图T(G)的加法度-基尔霍夫指标为:
定理1.20[16]设图G为n(n≥2)个顶点和m条边的连通图, 则三角剖分图T(G)的乘法度-基尔霍夫指标为:
Kf*(T(G))=6Kf+(G)+6m2-2mn.
定理1.21[16]设图G为n(n≥2)个顶点和m条边的连通图, 则迭代三角剖分图Tk(G)的乘法度-基尔霍夫指标为:
定理1.22[16]设图G为n(n≥2)个顶点和m条边的连通图, 则迭代三角剖分图Tk(G)的加法度-基尔霍夫指标为:
定理1.23[16]设图G为n(n≥2)个顶点和m条边的连通图, 则迭代三角剖分图Tk(G)的基尔霍夫指标为:
2016年, 刘晓刚等[17]给出了R-点联和R-边联的电阻距离和基尔霍夫指标的结果.
定理1.24[17]设图G1的顶点数为n1边数为m1, 图G2的顶点数为n2, 则

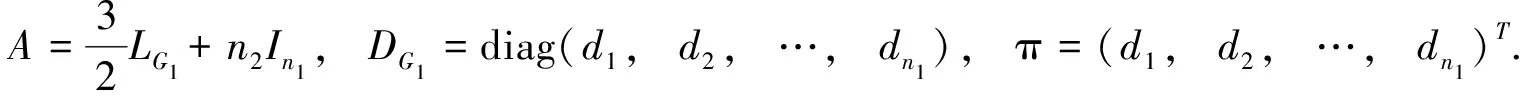
定理1.25[17]设图G1是n1个顶点和m1条边上的r-正则图(r>0), 图G2的顶点数为n2, 则
2016年, 卢鹏丽等[18]刻画了Q-图的电阻距离.刘群等[19]给出了R-点(边)冠图G1⊙G2(G1ΘG2)的基尔霍夫指标的公式和下界, 其中G1为正则图,G2为任意图.
定理1.26[19]设G1是一个具有n1个顶点和m1条边的r1-正则图,G2是一个具有n2个顶点的任意图, 则
定理1.27[19]设G1是一个具有n1个顶点和m1条边的r1-正则图,G2是一个具有n2个顶点的任意图, 则
此外, Xie等[20]还得到了简单连通图迭代剖分图的正规拉普拉斯谱, 作为应用的一个例子, 计算了它们的乘法度-基尔霍夫指标、 Kemeny常数和生成树数的精确值.
定理1.28[20]对于任意n>0,sn(G)和sn-1(G)的乘法度-基尔霍夫指标的关系如下:
Kf*(sn(G))=8Kf*(Sn-1(G))+2n(2r-1)E0,
因此,Kf*(sn(G))的一般表达式为:

其中r=E0-N0+1.
2021年, Sun等[21]刻画了Q-点(边)联图的电阻距离和基尔霍夫指标.
定理1.29[21]设G1和G2是两个图, 分别有n1(n2)个顶点m1(m2)条边, 如果G1是一个d-正则图, 那么G1
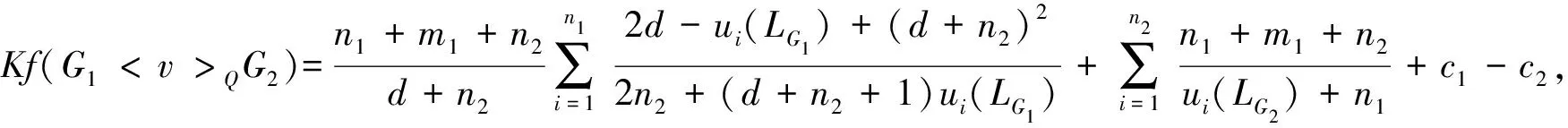
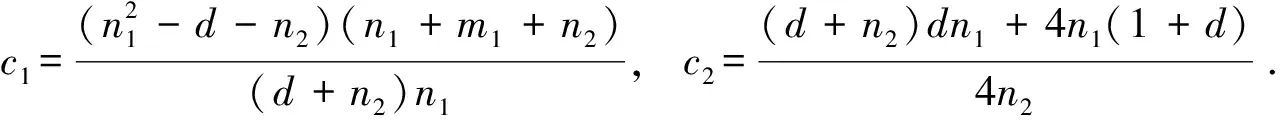
定理1.30[21]设G1和G2是两个图, 分别有n1(n2)个顶点m1(m2)条边, 如果G1是一个d-正则图, 那么G1
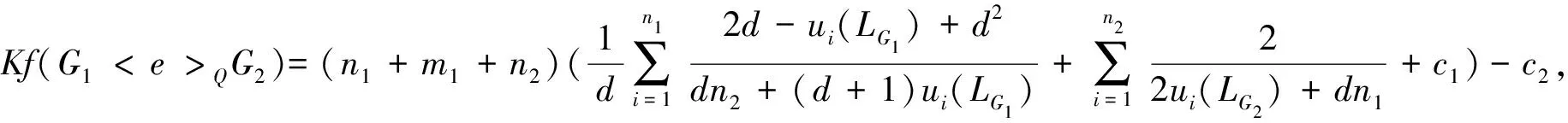
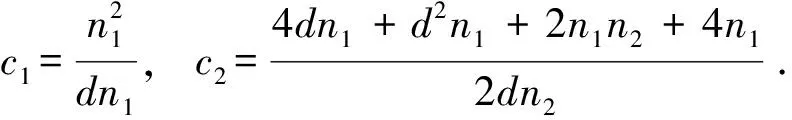
2 特殊图类的(乘法度-)基尔霍夫指标
因为对于一般图的基尔霍夫指标计算较困难, 所以只给出了一些特殊图类的结果, 如Nordhaus-Gaddum[22]结论、 单圈图的基尔霍夫指标、 双圈图的基尔霍夫指标.
2.1 基尔霍夫指标的Nordhaus-Gaddum类型结论
等式(在下界)成立当且仅当G是会议图时.
虽然上界几乎是最好的可能, 但它是不可达到的. 对于上界, 他们提出如下猜想:

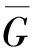
2016年, Das和杨玉军[25]考虑了3种基于电阻距离的图不变量, 即基尔霍夫指标、 加法度-基尔霍夫指标和乘法度-基尔霍夫指标, 给出了基于阻力距离的图不变量的Nordhaus-Gaddum型的一些结果, 并建立了这些基尔霍夫指标之间的关系.
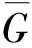
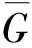
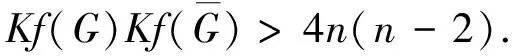
定理2.5[25]设G是一个n阶连通图, 有m条边, 最大度和最小度分别为Δ和δ, 则
2(n-1-δ)(2Δ+5-n)m.
定理2.6[25]设G是一个n阶连通图, 有m条边, 最大度Δ 定理2.7[25]设G是一个n阶连通图, 有m条边, 最大度和最小度分别为Δ和δ, 则 m(n-1-δ)2(2Δ+5-n). 定理2.8[25]设G是一个n阶连通图, 有m条边, 最大度Δ>1, 最小度δ>1, 则 2018年, 杨玉军等[26]利用电学和组合技术证明了文献[24]的猜想除5个顶点上的树图外, 对所有图都是正确的. 若图G只包含一个圈, 则称为单圈图. 为方便起见, 用G=U(Cl;T1,T2, …,Tl)表示, 其中Cl是G中唯一的圈. 设V(Cl)={v1,v2, …,vl}满足对1≤i≤l,vi和vi+1相邻, 对每个i, 令Ti为G中删掉圈上除vi以外的所有点后得到的图中包含vi的分支. 2008年, 杨玉军等[27]研究了单圈图的基尔霍夫指标的界, 并给出了一些特殊单圈图的基尔霍夫指标公式. 如: 定理2.10[27]在所有的n个顶点的单圈图中: 1)若n<8, 则Cn达到最小的基尔霍夫指标; 定理2.11[27]对顶点数为n的单圈图G: 2011年, 文献[9]首次给出超基尔霍夫指标的概念, 并给出了超Kirchhoff指标的下界和上界, 同时确定了当n≥5时具有最小、 次小和第三小超Kirchhoff指标和最大、 次大和第三大超Kirchhoff指标的n顶点单圈图. 此外, 还确定了圈长为s(3≤s≤n)的n阶单圈图的最小和最大的超基尔霍夫指标. 2012年, 文献[8]首次给出加法度-基尔霍夫指标的概念, 并刻画了具有最小和次小加法度-基尔霍夫指标的n个顶点的单圈图. 一个单圈图称为是满载单圈图, 如果它的圈上的每个顶点的度都不小于3. 2009年, Guo等[28]确定了满载单圈图的基尔霍夫指标的界并且刻画了达到界的极值图. 定理2.12[28]设G是顶点数n≥6的满载单圈图, 则 等式成立当且仅当n=8时G=U(C4;K2,K2,K2,K2);当n≠8时G=U(C3;K2,K2,Sn-4). 定理2.13[28]设G是顶点数n≥6的满载单圈图, 则 等式成立当且仅当G=U(C3;K2,K2,Pn-4). 2014年, Feng等[29]刻画了满载单圈图的最大和最小乘法度-基尔霍夫指标和仙人掌图的最小乘法度-基尔霍夫指标. 定理2.14[29]设G是n(≥6)阶的满载单圈图, 则 Kf*(U(C3;K2,K2,Sn-4))≤Kf*(G)≤Kf*(U(C3;K2,K2,Pn-4)), 左边等号成立当且仅当G≅U(C3;K2,K2,Sn-4), 右边等号成立当且仅当G≅U(C3;K2,K2,Pn-4). 2020年, Qi等[30]确定了n阶具有固定最大度的单圈图的极大乘法度-基尔霍夫指标, 以及n阶单圈图的前7个极大乘法度-基尔霍夫指标, 并得到了相应的极图. 定理2.15[30]设U(n,Δ)为n个顶点最大度为Δ的单圈图集合, 其中2≤Δ≤n-1, 设U′(n,Δ)是将C3的顶点与Δ顶点上的星中心连接, 路径长度为n-Δ-2得到的单圈图, 则 2020年, Chen等[31]得到了树和单圈图的补图的Kirchhoff指标的排序, 并给出了基尔霍夫指标的一个上界. 定理2.16[31]设G是一个有n个顶点m条边的连通图, 则 2021年, Chen等[32]用单圈图的剖分图的匹配数刻画了单圈图的Kirchhoff指标. 定理2.17[32]对于任意n阶连通单圈图G, 它有一个Ck(圈长为k), 其Kirchhoff指标Kf(G)可以表示为: 其中m(S(G),n-2)为单圈图的剖分图S(G)有n-2条边的匹配数,S(G)-C2k为S(G)中删除圈C2k的所有顶点而得到的无圈图. 2009年, 张和平等[33]给出了恰有两个圈的双圈图的基尔霍夫指标的界, 并刻画了达到界的极值图. 定理2.18[33]在所有顶点数为n的恰有两个圈的双圈图中: 定理2.19[33]对顶点数为n的恰有两个圈的双圈图G: 等式成立当且仅当G≅θ5(n-5, 0, 0, 0, 0). 2016年, 刘家保等[35]刻画了具有最小基尔霍夫指标的双圈图, 并确定了双圈图的基尔霍夫指标的界. 定理2.22[35]设G∈βn, 则 2018年, Fei等[36]刻画了n(≥6)阶的双圈图的最大乘法度-基尔霍夫指标和n(≥7)阶的双圈图的次大乘法度-基尔霍夫指标. 定理2.23[36]设G是一个n(n≥6)阶双圈图, 则 等式成立当且仅当G≅Bn. 定理2.24[36]设G是一个n(n≥7)阶双圈图且G不同构于Bn, 则 特别地, 2013年Deng等[37]得到了由G的剖分图的闭游动数表示的基尔霍夫指标的表达式, 并确定了树的补图的基尔霍夫指标的第一和第二最大值. 定理2.25[37]设G是一个具有n(n≥2)个顶点和m条边的二部图, 则 定理2.26[37]设T是一个有n(n≥2)个顶点的树, 则 左边等号成立当且仅当T是Sn时, 右边等号成立当且仅当T是Pn. 本节我们将确定一些图的基尔霍夫指标的界, 并且刻画达到界的极值图. 2010年, Palacios等[38]给出了n个顶点的d正则图的基尔霍夫指标上下界. 命题3.1[38]对任意n个顶点的k正则图, 有 如果图是二部图, 则下界可进一步改进为: 2011年, Palacios等[39]给出了当G是任意连通图时, 基尔霍夫指标的界为: 其中1=λ1(P)>λ2(P)≥…≥λn(P)≥-1是转移矩阵P=D-1A的特征值. 2013年, Das[40]得到Kf(G)的下界取决于顶点数n, 最大度Δ, 生成树数t: 等式成立当且仅当G≃Kn或G≅K1, n-1. 定理3.1[41]设G是一个具有n≥2个顶点和m条边的简单连通图. 如果G是d-正则图, 1≤d≤n-1, 则 定理3.2[42]设G是一个具有n≥3个顶点和m条边的简单连通图, 则 定理3.3[42]设G是一个具有n≥3个顶点和m条边的简单连通图, 则 等式成立当且仅当G≅Kn. 定理3.4[42]设G是一个具有n≥2个顶点和m条边的简单连通图, 则 等式成立当且仅当G≅Kn. 定理3.5[42]设G是一个具有n≥2个顶点和m条边的简单连通图, 对于任意具有性质un-1≥k>0的实数k, 有 等式成立当且仅当k=n和G≅Kn, 其中t为生成树的个数. 2012年, Yan等[43]刻画了正则图G的迭代线图Lk(G)和迭代抛物线图Ck(G)(或团插入图)的近似基尔霍夫指标. 定理3.6[43]设G是一个有n个顶点的连通的简单r-正则图, 则 定理3.7[43]设G是一个有n个顶点的连通的简单r-正则图, 则 2017年, 田贵贤[44]刻画了正则图的迭代全图的近似(乘法度-)基尔霍夫指标. 定理3.8[44]设G是一个有n个顶点m条边的连通r-正则图r≥2, 则 因此正则图的迭代全图的Kirchhoff指标的近似值与G的结构无关, 只与r和G的顶点数有关. 推论3.1[44]设G是一个有n个顶点m条边的连通r-正则图r≥2, 则 因此正则图的迭代全图的Kirchhoff指标的近似值与G的结构无关, 只与r和G的顶点数有关. G的边k-部图是删除使G成为k-部图的最小边数, 用lk(G)表示. 设m≤n-k,n,m,k是具有n个顶点且lk(G)≤m的图族, 即 ψn, m, k={G: |V(G)|=n,lk(G)≤m}, 如果k=2, 称为G的边二部图. 2017年, He等[45]给出了关于ψn, m, k的Kirchhoff指标最小化的第一个结果, 其中刻画了ψn, m, 2中的最优图. 2019年, Huang等[46]给出了给定边k-部图的最小基尔霍夫指标的理论和计算方法. 这里设n=pk+q, 其中p,q是非负整数, 且0≤q 在化学图论中, 一些化合物可以用化学图来表示, 其中顶点代表原子, 而边代表原子间的共价键. 此外, 预测化合物的物理化学性质一直是理论化学的研究热点, 因此下面列出一些线性链网络图的电阻距离和基尔霍夫指标的研究结果. 近年来, 相关学者已经计算了许多线性链的电阻距离、 基尔霍夫指标和加法度(乘法度-)基尔霍夫指标. 例如, 线性多边形链、 线性六角形链、 六角形链、 梯形图、 梯形链、 线性多项式链等. 2020年, Zhang等[47]刻画了随机聚苯乙烯链的舒尔茨指标、 古特曼指标、 乘法度-基尔霍夫指标和加法度-基尔霍夫指标的期望值. 定理4.1[47]设n≥1, 则随机聚苯乙烯链Gn的乘法度-基尔霍夫指标的期望值为: 定理4.2[47]设n≥1, 则随机聚苯乙烯链Gn的加法度-基尔霍夫指标的期望值为: 2021年, Zhang等[48]建立了方差的显式解析表达式, 以及随机聚苯乙烯链的古特曼指标、 舒尔茨指标、 可乘度基尔霍夫指标和可加度基尔霍夫指标, 并且证明了随机聚苯乙烯链的这4个指标是渐近正态分布. 李佳建和王维忠[49]通过求解差分方程, 建立了随机多边形链中基尔霍夫指标、 乘法度-基尔霍夫指标和加法度-基尔霍夫指标期望值的显式解析表达式. 定理4.3[49]设PCn是一个n长的(2k+1)-多边形链, 其中k≥1且n≥2, 则 定理4.4[49]设PCn是一个n长的(2k+1)-多边形链, 其中k≥1且n≥2, 则 定理4.5[49]设PCn是一个n长的(2k+1)-多边形链, 其中k≥1且n≥2, 则 定理4.6[49]设PCn是一个n长的2k-多边形链, 其中k≥2且n≥2, 则 定理4.7[49]设PCn是一个n长的2k-多边形链, 其中k≥2且n≥2, 则 定理4.8[49]设PCn是一个n长的2k-多边形链, 其中k≥2且n≥2, 则 2020年, 彭颖君[50]研究了线性六四角链、 线性八四对角链、 Möbius线性六四环链的(乘法度-)基尔霍夫指标. 近年来, 关于网络图的基尔霍夫指标的研究吸引了许多研究者的注意, 如:有线网络、 集群网络、 电晕或星团网络、 星形和锥形网络等. 特别地, 2020年, Huang等[51]得到了线性六边形(圆柱形)链的电阻距离和基尔霍夫指标公式, 并给出了线性六边形(圆柱形)链电阻距离的单调性和一些渐近性质;Sardar等[52]得到了链硅酸盐网络和环硅酸盐网络的电阻距离和基尔霍夫指标公式. 2021年, Palacios等[53]刻画了高对称图簇的Kemeny常数和基尔霍夫指标公式;Kook等[54]给出了单纯网络的基尔霍夫指标的计算公式, 利用此公式得到了代数连通性和基尔霍夫指标的高维类似物的一个不等式, 并提出这些量作为单纯复形鲁棒性的度量. 2006年, Gutman和周波[55]定义了图G的拉普拉斯能量: 2008年, 柳柏濂等[56]定义了图G的拟拉普拉斯能量: 2012年, Das等[57]比较了Kf(G)和LEL(G), 并建立了LEL(G) LEL(G) LEL(G) 2018年, Das和Gutman[58]得到了拟拉普拉斯能量LEL与基尔霍夫指标Kf、 拉普拉斯能量LE与基尔霍夫指标Kf的两个关系. 定理4.11[58]设G是一个有m条边的n(>2)阶连通图,Δ为顶点最大度, 则 等式成立当且仅当G≅Kn或G≅K1, n-1. 定理4.12[58]设G是一个有m条边的n(>2)阶连通图, 则 其中u1≥k≥Δ+1(Δ为顶点最大度). 定理4.13[58]设G是一个有m条边的n阶连通图, 则 定理4.14[58]设G是一个有m条边的n(>2)阶连通图, 则 Kf(G)(M1(G)+2m)≥nLEL2(G), 等式成立当且仅当G≅Kn. 定理4.15[59]设G是一个有m条边的n(≥2)阶连通图, 则 定理4.16[59]设G是一个有m条边的n(≥2)阶连通图, 则 nLEL4(G)≤8m3Kf(G), 等式成立当且仅当G≅Kn. 定理4.17[59]设G是一个有m条边的n(≥2)阶连通图, 则 等式成立当且仅当G≅Kn, 或G≅K1, n-1, 或G≅Γd. 定理4.18[59]设G是一个有m条边的n(≥2)阶连通图, 则 等式成立当且仅当G≅Kn, 或G≅K1, n-1, 或G≅Γd. 定理4.19[59]设G是一个有m条边的n(≥2)阶连通图, 则 8m3(Kf(G)+1)-n2(n-1)S2(G)≥4n2(n-1)m2, 等式成立当且仅当G≅Kn或G≅Γd. 定理4.20[59]设G是一个有m条边的n(≥2)阶连通图, 则 等式成立当且仅当G是正则图. 对于一些特殊图类, 如赋权图、 赋权轮图、 具有固定割顶点数的图、 完全多部图、 莫比乌斯阶梯(Mn=C2n(1,n))和棱镜图(Prn=Cn×P2)[60]的Kirchhoff指标也分别得到了刻画. 特别地, 2018年Mitsuhashi等[61]首次提出加权基尔霍夫指标, 并给出正则覆盖图的基尔霍夫指标;2021年, Lin等[62]给出了混合图的埃尔米特基尔霍夫指标与鲁棒性;2017年, 刘家保[63]在《电阻距离和基尔霍夫指标的研究》中刻画了双圈图、 仙人掌图、 超立方体网络等的基尔霍夫指标, 并得到了一些新的有意义的结果. 定理4.21[60]莫比乌斯阶梯(Mn=C2n(1,n))的基尔霍夫指标为: 定理4.22[60]棱镜图(Prn=Cn×P2)的基尔霍夫指标为: 1)2020年, 文献[46]研究了在n,m,k中求最小基尔霍夫指标的问题, 即求最小值给定k-分布性图的基尔霍夫指标. 该文章从理论上部分地解决了这个问题, 并提出了采用包括穷举搜索和3种计算策略在内的算法来解决问题. 然而, 在n,m,k中具有最小基尔霍夫指标的最优图的完全刻画问题尚有待进一步解决. 2)文献[50]的最后提出了一些尚待解决的问题: (a)可以进一步考虑对有一个割点的线性六四角链的分子图的拉普拉斯谱以及基尔霍夫指标和支撑数目的研究; (b)可以进一步考虑对Möbius线性八四对角链的拉普拉斯谱及基尔霍夫指标和支撑树数目, 以及正规拉普拉斯谱及度基尔霍夫指标与支撑数目的研究; (c)可以进一步对四边形、 六边形及八边形在一个线性链中同时出现或对非线性及其他边形的角链类型的相关问题进一步研究. 3)在第2节中, 就单圈图而言, 可以考虑加一些限制条件的单圈图, 如具有完美匹配的单圈图和确定悬挂点个数的单圈图. 对于双圈图, 可以继续考虑具有3个圈的双圈图的基尔霍夫指标. 4)2021年, 文献[54]中提出了一个开放的问题, 并给出下列恒等式的组合证明: 5)2020年,文献[64]中的定理6认为在所有具有任意固定直径的二部图中,基尔霍夫指标最小和最大的图可以用同样的方法确定.但是在所有直径大于3的二部图中刻画第二小、第三小以及第二大和第三大的基尔霍夫指标将是一个非常具有挑战性的问题.
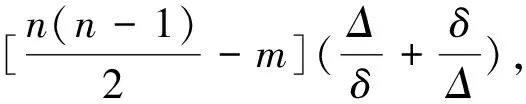
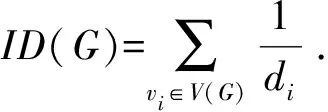
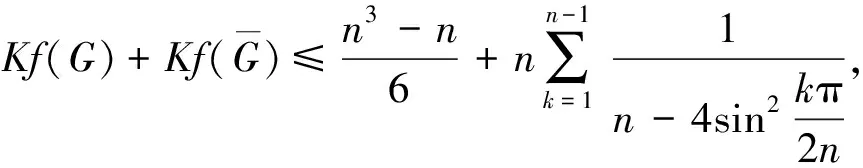
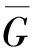
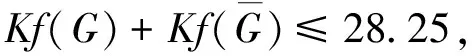
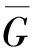
2.2 单圈图的基尔霍夫指标

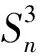



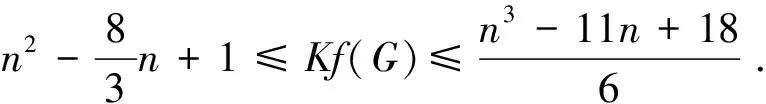
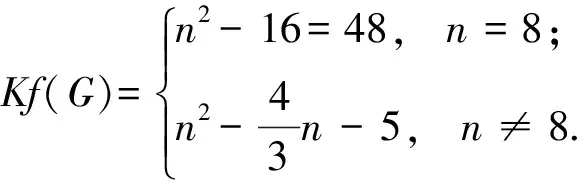
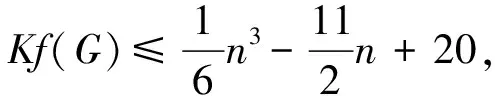
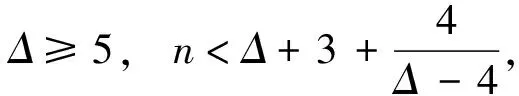
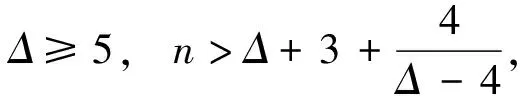
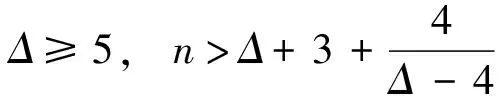
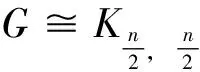
2.3 双圈图的基尔霍夫指标
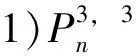


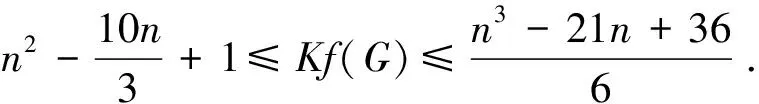
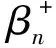

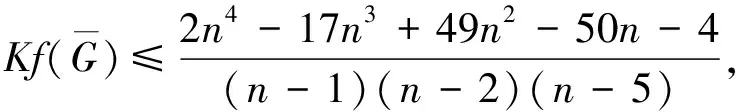
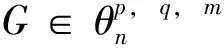

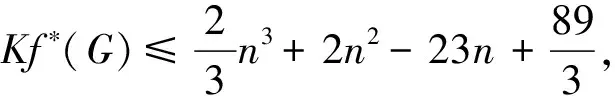
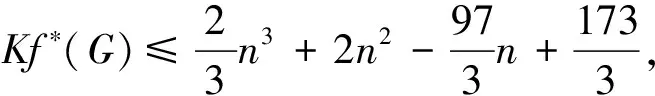



3 基尔霍夫指标的界
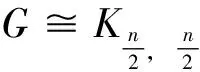


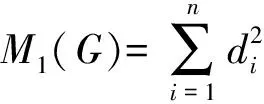
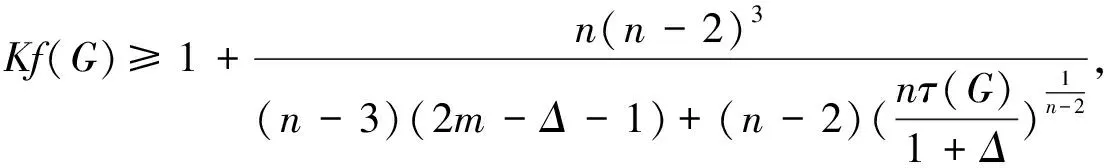
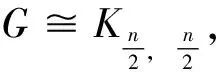
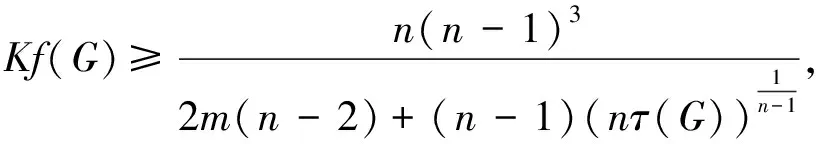
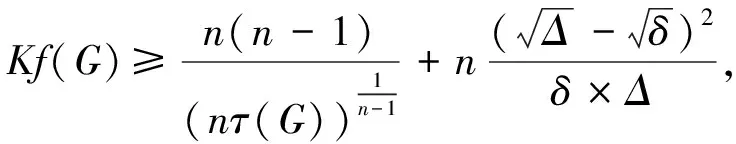


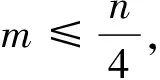

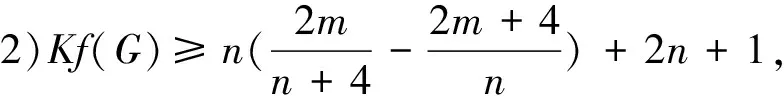
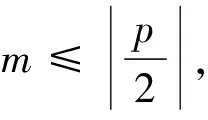

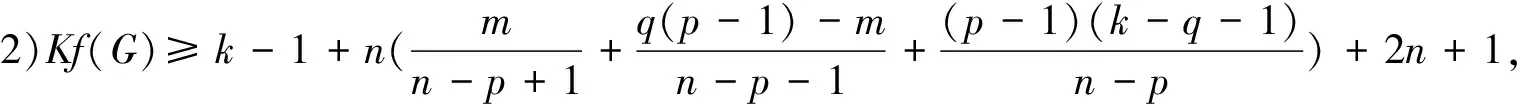
4 基尔霍夫指标的应用
4.1 线性链和网络图的基尔霍夫指标
4.2 基尔霍夫指标与其他指标的关系
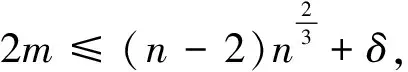
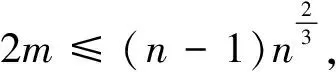
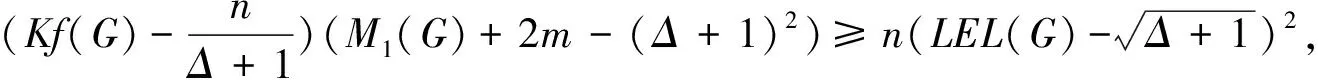
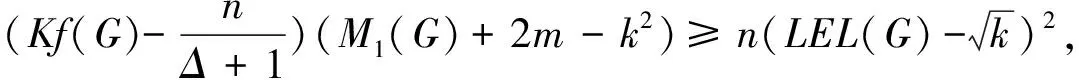
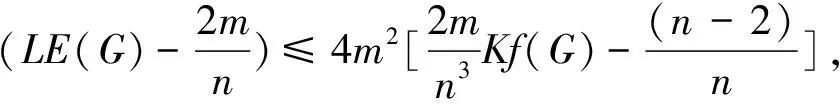
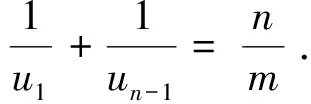




5 一些猜想和未解决的问题
