基于自适应遗传算法优化非对准误差补偿算法

杨宗林， 陈晓勇,2,3， 熊继军,2， 张晓明,2， 洪应平,2

(1. 中北大学 仪器科学与动态测试教育部重点实验室， 山西 太原 030051；2. 中北大学 电子测试技术重点实验室， 山西 太原 030051； 3. 中北大学 化学工程与技术学院， 山西 太原 030051)

0 引 言

随着现代科技的发展， 各国开始关注地震破坏、 高能爆破和强撞击等特殊危害的精准评估及极端冲击动力学研究. 三轴加速度计广泛应用于极端或常规冲击和振动信号监测、 撞击点定位、 波场重建以及目标损伤评估等方面的研究. 三轴加速度计用于敏感载体三轴比力， 其性能好坏对解算监测和定位信息的准确性有直接影响， 由于三轴加速度计在转台上确定的标度因数矩阵与零位输出电压会随时间发生变化， 因此在无大型转台情况下， 现场标定补偿方法的研究具有重要意义.

目前， 国内外学者已提出了诸多针对三轴加速度计不正交角、 主轴灵敏度与零偏等的补偿方法， 例如最大似然数标定补偿方法[1-2]， 支持向量机的加速度计参数估计[3]， 椭球拟合法[4-5]， 自适应系数求解法[6-7], 自适应滤波算法[8]， 遗传算法[9-10]， 粒子群算法[11-12]， 神经网络[13-14]等参数估计方法. 其中椭球拟合法由于现场标定快速简易稳定而应用较多， 但是由于存在旋转模糊性， 其精度还是不能满足日益增加的应用需求.

为了提升三轴加速度计现场快速标度的精度， 本文通过对三轴加速度计进行标定误差分析， 引入传统椭球拟合标度补偿方法， 将旋转模糊性考虑进来， 提出了基于自适应遗传算法优化非对准误差矩阵的方法. 在实际使用椭球拟合的补偿方法时， 都会采取预先假设标度因数矩阵的三角矩阵的方式来解决旋转模糊问题. 然而， 在标定补偿中， 通常标度因数矩阵的形式是不可预知的， 因而椭球拟合补偿存在非对准误差. 本文通过椭球拟合方法引入非对准误差， 将旋转模糊问题作为研究对象， 通过自适应遗传算法对非对准误差进行参数估计.

1 三轴加速度计标定模型

1.1 三轴加速度计输出补偿模型

在实际测量中， 三轴加速度计的安装误差、 刻度因子以及测量噪声等因素会导致测量误差. 因此， 三轴加速度计的输出模型为

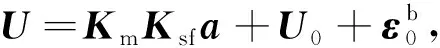
(1)

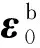
U=Ka+U0,

(2)

1.2 椭圆拟合标定模型

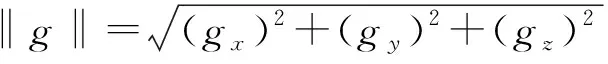
在室温下， 同一地点加速度恒定不变， 现假设现场的重力加速度的模为恒定g， 将式(2)输出模型转化为加速度校正模型，

a=K-1(U-U0)，

(3)

因此，

‖a‖=‖K-1(U-U0)‖=g.

(4)

对式(4)变换成标准二次型为

(U-U0)T(K-1)TK-1(U-U0)=g2.

(5)

令

M=(K-1)TK-1/g2，

(6)

联立式(5)和(6)， 得到广义的椭球面方程

(U-U0)TM(U-U0)=1.

(7)

将椭球方程表示为一般形式

2eUxUz+2fUyUz+2gUx+

2hUy+2iUz+2j=0,

(8)

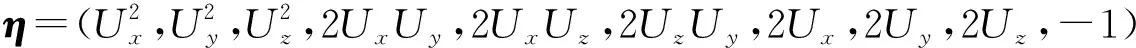
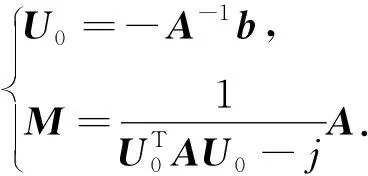
(9)

联立式(6)和(9)可得出标度因数矩阵的逆矩阵K-1.

1.3 三轴加速度计椭球拟合快速标定方法的不足

在1.2节中利用拟合的椭球面方程求解标度因数矩阵K时， (K-1)TK-1=Mg2需要做对称矩阵分解. 然而， 无论采用cholesky分解[16]、 特征值分解[17]或是其他方法， 都需要假设标度因数矩阵K为对角矩阵、 三角矩阵或对称矩阵的矩阵形式， 从而分解得到对角矩阵、 三角矩阵或对称矩阵的矩阵形式的标度因数矩阵的逆矩阵K-1. 一般情况下， 标度因数矩阵K没有确定的具体形式， 所以， 分解得到的标度因数矩阵的逆矩阵K-1是不准确的.

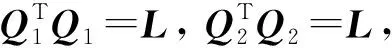
2 基于自适应遗传算法的非对准误差补偿方法

2.1 三轴加速度计输出椭球拟合补偿模型

从几何角度分析， 造成非对准误差的原因是存在一个正交矩阵R， 使得椭球拟合标定的三轴加速度计相对于载体坐标系旋转了某一个固定角造成的. 因此， 在椭球拟合的基础上， 假设三轴加速度计坐标分别绕z轴，y轴，x轴旋转固定的角度θ1,θ2,θ3变换到载体坐标系， 则非对准误差角为θ=(θ1,θ2,θ3)， 因此， 存在正交矩阵R(θ)为

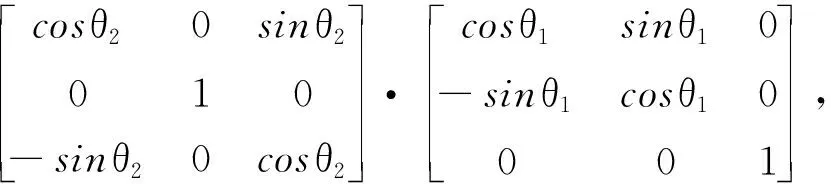
(10)

于是有

K′-1=R(θ)K-1.

(11)

利用式(3)将1.1节校正的三轴加速度计的输出电压转化为对应加速度g值， 记为a=[azi,ayi,azi]T,i=1,2,…,n， 则非对准误差补偿的加速度为

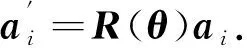
(12)

2.2 基于自适应遗传算法的非对准误差补偿方法

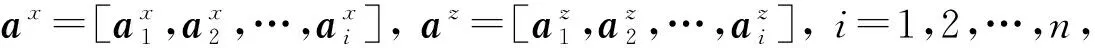
1) 编码. 将非对准误差矩阵R(θ)包含的3个未知数作为一条染色体上的9段基因， 用实数编码对种群中的全部基因进行初始化.

2) 计算适应值. 适应度函数的选区直接影响算法的收敛性能. 本文根据距离的平方和构造适度函

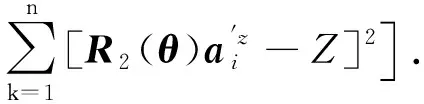
(13)

显然，L(θ)越趋近于零， 非对准误差角越接近实际值， 对测量值的补偿标定越准确， 所以， 目标函数为minL(θ).

3) 选择. 通过计算每一个适应度函数的适应度值得到每个个体的选择概率以及累加概率作为选择区间， 选择最优的个体复制到下一代种群中去.

4) 自适应交叉和变异. 交叉和变异是整个算法的核心， 传统算法中， 交叉概率过大会导致代沟大， 变成了随机算法， 而过小会导致停滞收敛太慢， 抑制早熟现象的能力就会较差； 变异概率过大也会使基因的遗传变得不稳定， 优良的基因容易被破坏， 变异概率过小导致个体稳定， 容易陷入局部收敛， 搜索不到全局最优. 因此提出自适应交叉和变异概率

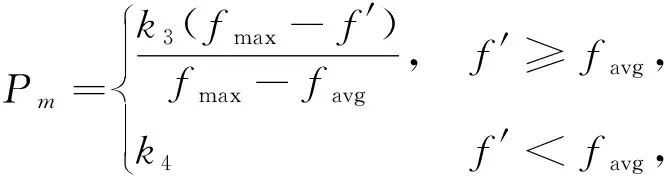
(14)

式中：fmax为种群中最大适应度值；favg为种群中平均适应度值；f为交叉个体中较大的适应度值；f′为变异个体的适应度值； 参数k1=k3=1,k2=k4=0.5.

5) 反复迭代3)、 4)步直至算法收敛， 适应度提升的空间很小， 计算出非对准误矩阵R(θ).

最后， 通过式(11)计算出准确的标定因数矩阵K和零位输出电压U0， 利用输出补偿模型对三轴加速度计进行现场快速标定.

3 算法性能分析

为了验证本文所提非对准误差参数估计方法的有效性和可行性， 在田晓春等[18]基于转台标定的标定因数矩阵K和零位输出电压U0基础上， 创建3组分别绕x轴，y轴，z轴旋转半径为1个g的标准球面数据， 如图 1 所示.

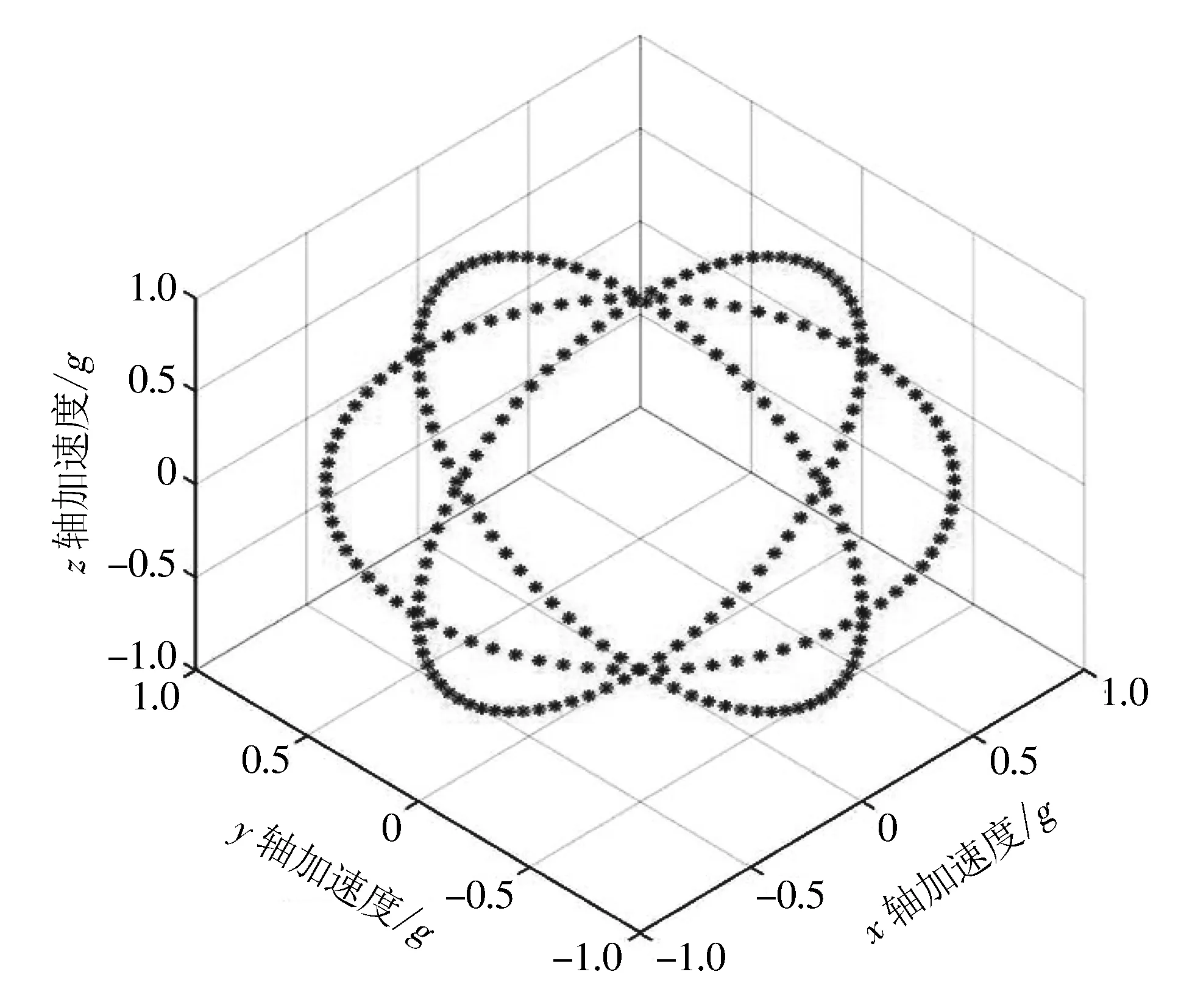
图 1 标准球形三轴加速度Fig.1 Standard spherical triaxial acceleration

将标定因数矩阵K和零位输出电压U0代入输出电压模型， 把标准的数据球面转化为椭球面的实测数据， 如图 2 所示. 从图中可以看出， 标准的球面数据转变成了球心不在原点的椭球面数据， 下面使用这些数据验证本文算法的可行性.

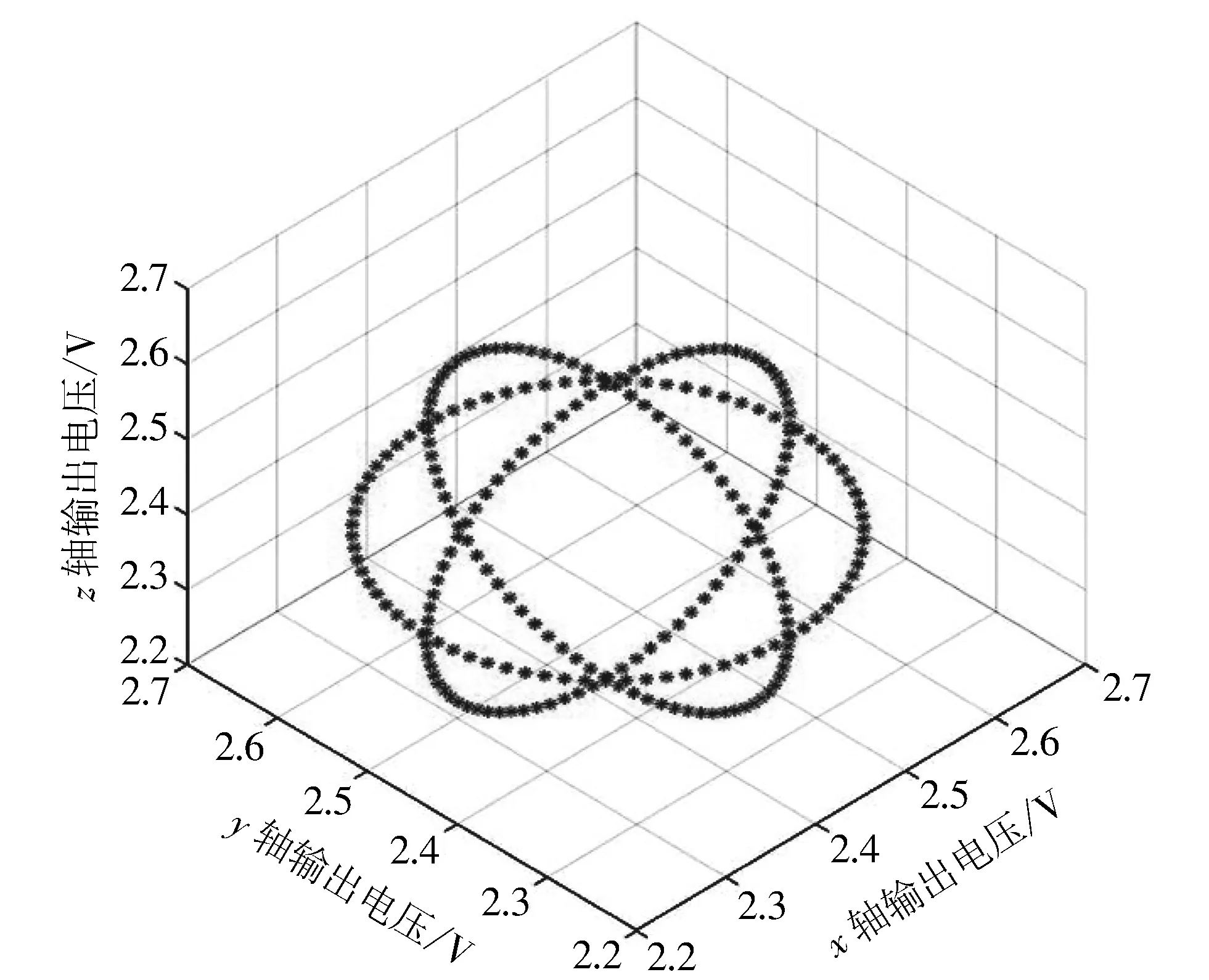
图 2 椭球面加速度计实际输出电压Fig.2 Actual output voltage of ellipsoidal accelerometer

创建测试数据后， 采用椭球拟合对三轴加速度计进行标定补偿结果与原始数据的比对图如图 3 所示.

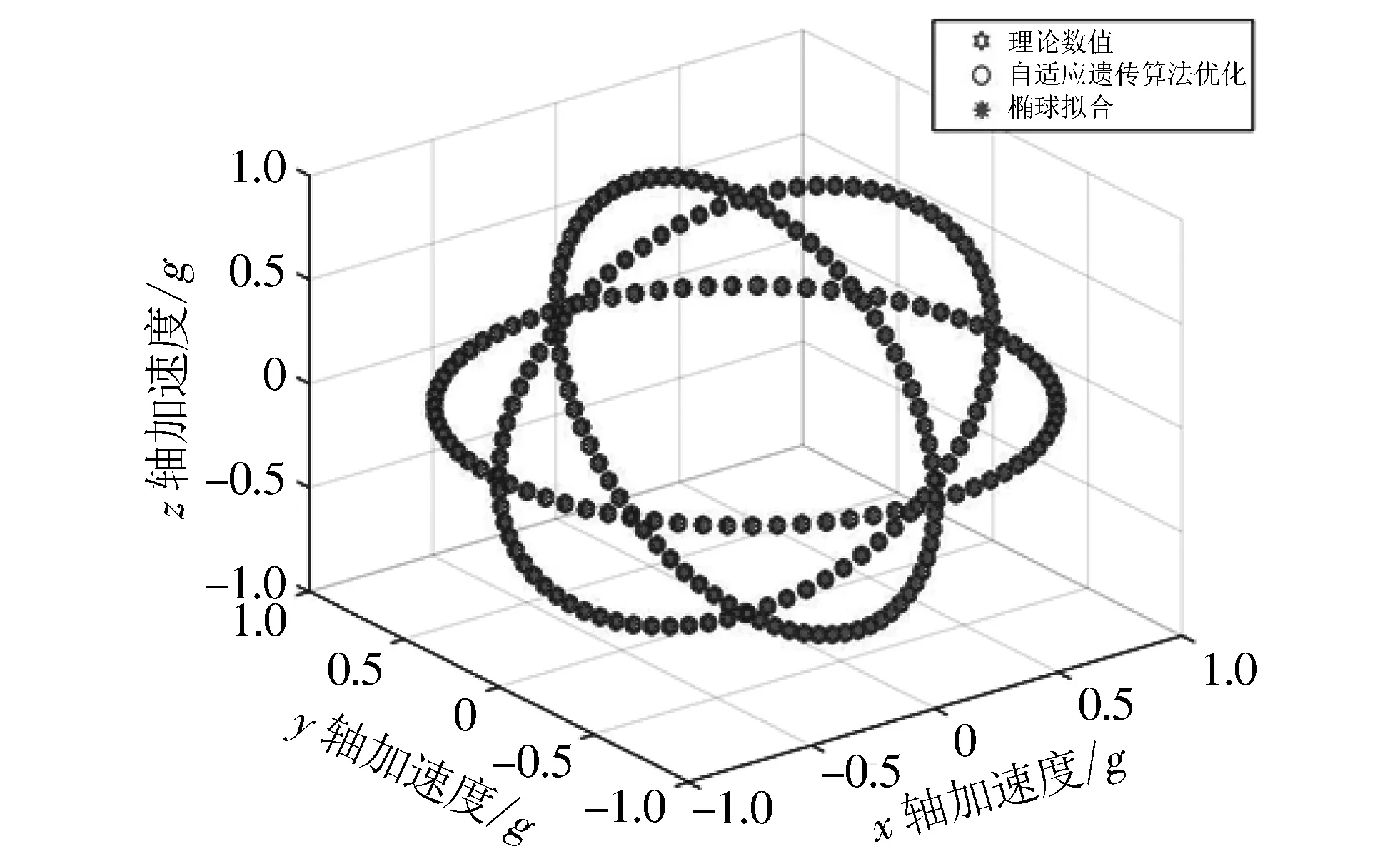
图 3 三轴加速度计标定补偿结果Fig.3 Calibration compensation results of triaxial accelerometer

通过自适应遗传算法搜索全局最优适应度值， 快速收敛到全局最优解， 非对准误差参数估计全部实现收敛， 椭球拟合补偿的3个轴的均方误差分别为1.412 3e-05， 1.424 3e-05， 6.774 6e-08； 本文所提方法补偿非对准误差后， 3个轴的均方误差分别为1.347 0e-11， 1.383 5e-11， 1.920 2e-11. 从各个轴向的精度来看， 精度最大提升了6个数量级， 因此自适应遗传算法可以很好地应用在三轴加速度计非对准误差参数估计中. 图 4 为最优适应度与平均适应度值随迭代次数变化情况， 最终结果趋近于零.

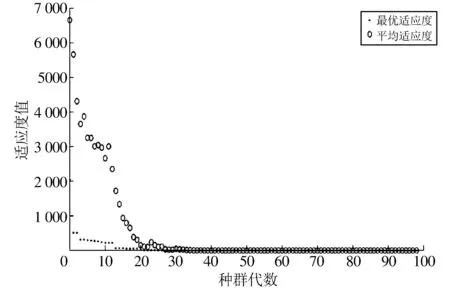
图 4 适应度收敛过程Fig.4 Convergence process of fitness

由于上述数据不正交角和零位输出电压都较小， 而且标定的环境干扰较少， 因此数据误差不大， 旋转模糊性导致的非对准误差显示不明显. 本文基于标准球面经过伸缩、 平移、 旋转以及测量噪声畸变成不标准椭球的原理， 创建出带有噪声的一般椭球面， 再利用本文所提方法进行标定补偿， 结果如图 5 所示. 在数据畸变较大的情况下， 椭球拟合补偿的非对准误差影响很明显， 椭球拟合补偿的3个轴的均方误差分别为0.056 0， 0.204 6， 0.164 3； 本文所提方法补偿非对准误差后， 3个轴的均方误差分别为0.001 1， 4.307 5e-04， 5.037 7e-04， 验证了基于椭球拟合的标定方法存在非对准误差的缺陷以及本文所提非对准误差估计方法的有效性， 并且在观测数据受到较大干扰时， 精度提升了2个数量级， 表现出良好的补偿精度.

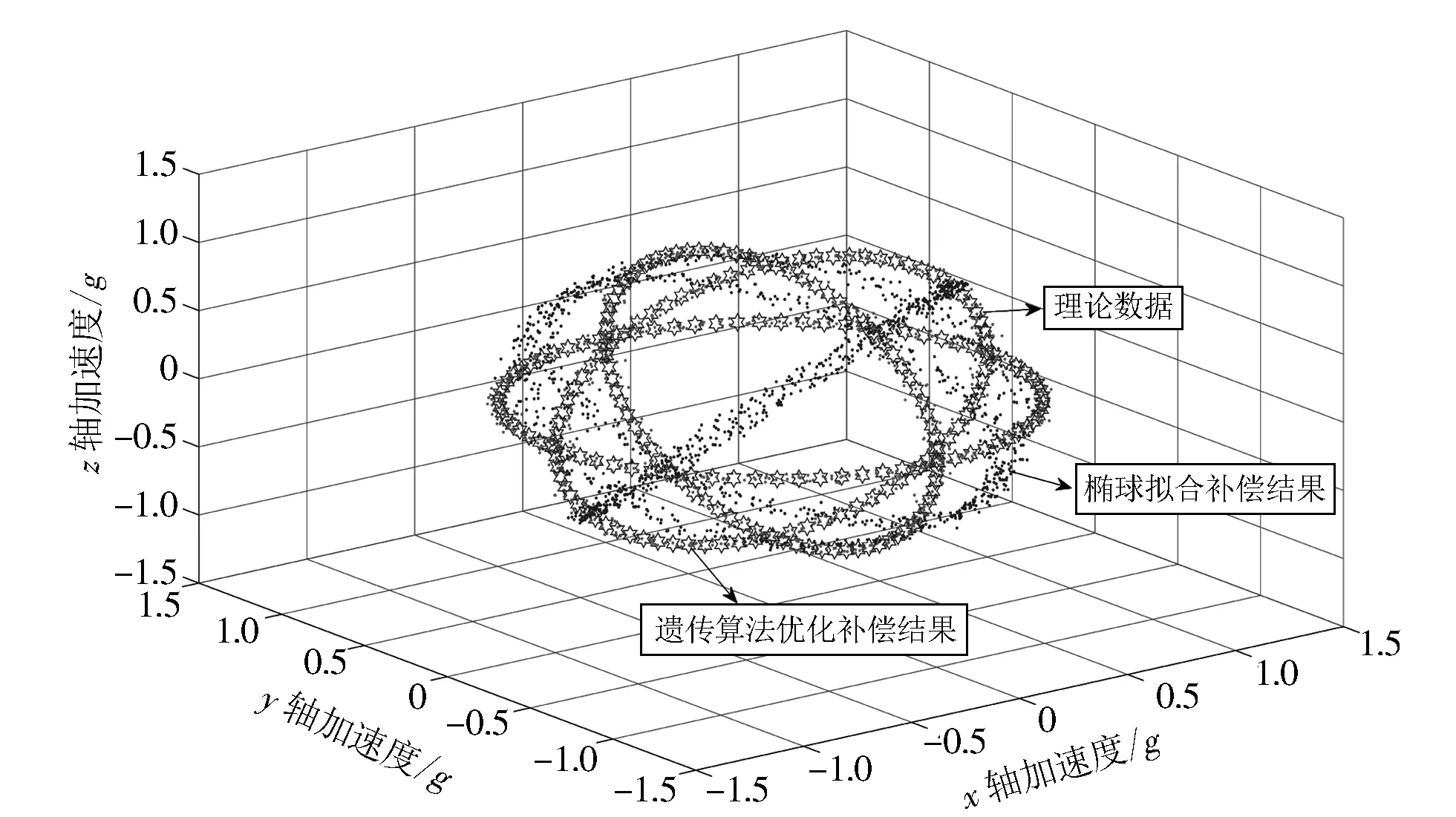
图 5 不良数据下三轴加速度计标定补偿结果Fig.5 Calibration compensation results of triaxial accelerometer in bad data

4 结 论

本文所提算法在传统椭球拟合的基础上引入自适应遗传算法非对准误差估计， 解决了旋转模糊问题. 仿真结果表明， 本文所提补偿算法对三轴加速度计补偿标定的精度均方误差达到了 0.001 的误差精度， 在数据良好时， 误差均方误差精度达到了10-11. 在数据干扰较大时， 该算法对非对准误差的补偿表现良好， 解决了传统椭球拟合旋转模糊的问题， 并且有良好的鲁棒性和精度.