基于ARM的SINS/GNSS紧组合导航系统设计

王树森， 张 鹏， 李孟委,2

(1. 中北大学 仪器与电子学院， 山西 太原 030051； 2. 中北大学 电子测试技术重点实验室， 山西 太原 030051)

0 引 言

目前应用最为广泛的导航系统是捷联惯性导航系统(Strapdown Inertial Navigation System, SINS)与全球卫星导航系统(Global Navigation Satellite System, GNSS). SINS具有可靠性高、 隐蔽性好、 体积小等优势[1-2]， 但是其定位误差会随时间而积累； GNSS具有全球性、 高精度、 全天候、 实时导航等优点， 但卫星信号容易被遮挡， 动态性能和可靠性较差， 不能输出载体的姿态信息[3]. SINS/GNSS组合系统可以利用SINS与GNSS的优势来弥补各自在导航性能上存在的缺陷， 不仅能够输出更加全面的参数信息， 而且可以提高系统精度与鲁棒性[4].

SINS/GNSS组合系统采用的松组合方式原理与结构相对简单， 算法与工程上也相对容易实现[5]. 然而， 当GNSS信号受到干扰失锁， 可见卫星数量少于4颗时， 没有GNSS系统稳定的输出对SINS系统输出进行修正， 松组合导航只能依靠纯捷联惯性导航解算， 导航精度难以满足实际应用需要. SINS/GNSS紧组合导航采用伪距和伪距率组合方式， GNSS卫星负责输出所得原始伪距、 伪距率信息和星历数据， 不用进行GNSS导航解算， 系统的鲁棒性好， 精度更高， 且当GNSS信号受到干扰失锁， 可见卫星数少于4颗时， 仍能够使用仅有的GNSS卫星数据辅助SINS进行数据融合完成导航定位. 超紧组合的导航精度虽然更高， 但GNSS卫星接收机需要矢量跟踪与反馈环路， 工程不容易实现[6]. 由于系统的状态与量测方程均为非线性的， 其线性化过程中的线性化误差会导致滤波精度降低， 而无迹卡尔曼滤波(Unscented Kalman Filter， UKF)算法能够避免非线性系统线性化的过程， 具有鲁棒性好、 精度高等优点[7]. 因此， 本文选用UKF算法对系统数据进行融合处理， 并设计了基于ARM的SINS/GNSS紧组合导航系统.

1 组合导航系统总体设计

基于ARM的紧组合系统， 采用三星Exynos4412微处理器作为原始数据采集、 捷联解算和数据融合的核心， 惯性测量单元(Inertial Measurement Unit， IMU)采用MPU9250， 陀螺噪声为0.06 °/s， 加速度计噪声为4 mg. GNSS接收机采用MH16-T1， 可以输出1 PPS秒脉冲及伪距、 伪距率与星历等原始观测信息， 时间精度(1 PPS)达到±20 ns， 原始数据的伪距观测精度可达到0.3 m， 系统的总体设计方案如图 1 所示.

图 1 系统总体设计方案Fig.1 Overall system design

硬件系统选用Exynos4412作为核心， Exynos4412微处理器利用SPI接口实时采集IMU模块产生的三轴加速度、 角速度与磁力计信息， 利用UART接口将GNSS接收机产生的星历数据与伪距、 伪距率信息以及1 PPS秒脉冲传输到Exynos4412微处理器. 对接收到的原始数据进行预处理和导航初始化， 根据初始的IMU信息进行初始对准， 得到初始速度、 位置和姿态信息， 然后再进行捷联解算. 当微处理器收到PPS秒脉冲和GNSS数据时， 进行SINS伪距、 伪距率计算并将计算结果转换至地心地固坐标系(Earth-Centered, Earth-Fixed, ECEF)， 用UKF算法对紧组合数据进行融合处理， 修正SINS解算的误差， 并在上位机上显示组合导航信息.

由于GNSS接收机与IMU模块是两个独立的模块， 其各自的数据更新频率不同， 为保证数据融合时的SINS和GNSS数据来自同一时刻， 每当GNSS接收机MH16-T1输出的1 PPS秒脉冲送入ARM微处理器时会引发中断， 定时器发生重置. 在无秒脉冲输入时， 定时器每隔10 ms向MPU-9250获取IMU数据， 在收到秒脉冲后定时器会进行重置， 从而完成GNSS和SINS数据的时间同步.

2 SINS/GNSS紧组合非线性模型

2.1 紧组合导航算法流程

图 2 为SINS/GNSS紧组合算法流程图. SINS/GNSS紧组合算法由捷联惯性导航SINS算法与UKF算法两种构成[8]. 其中， SINS采用自对准算法进行粗对准和精对准， 采用旋转矢量的三子样算法进行捷联姿态更新. SINS/GNSS紧组合采用伪距和伪距率组合方式， 其中GNSS模块只负责输出所测伪距和伪距率信息以及对应星历数据. SINS模块由IMU输出原始数据， 经过捷联解算后， 再根据星历数据进行SINS伪距和伪距率计算. 最后， 使用UKF算法对SINS模块与GNSS接收机模块的数据进行融合， 在误差补偿后输出组合导航信息[9-10].

图 2 GNSS/SINS紧组合算法流程图Fig.2 GNSS/SINS tight combination algorithm flow chart

2.2 紧组合系统状态方程

系统状态误差矢量为

X(t)=[φE,φN,φU,δνE,δνN,δνU,δL,δλ,δh,

εbx,εby,εbz,εrx,εry,εrz,x,y,z,δtu,δtru]T,

(1)

式中：φE,φN,φu为姿态误差角；δνE,δνN,δνU分别为东北天向速度误差；δL,δλ,δh分别为经度、 纬度和高度误差；εbx,εby,εbz为陀螺仪随机误差；εrx,εry,εrz为陀螺仪的一阶马尔科夫过程；x,y,z为加速度计零偏；δtu为GNSS时钟误差引起的距离误差；δtru为GNSS时钟频率误差引起的速度误差.

SINS/GNSS紧组合系统误差状态方程由SINS误差状态方程与GNSS误差状态方程构成

(2)

即

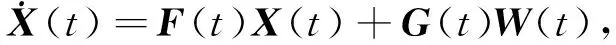
(3)

式中：

(4)

(5)

FN为9阶惯导误差方阵，

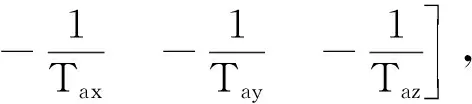
(6)

Tgi,Tai(i=x,y,z)分别为陀螺仪与加速度计所对应的一阶马尔可夫相关时间常数，

(7)

2.3 紧组合系统量测方程

选取SINS计算的伪距和伪距率与GNSS提供的伪距和伪距率分别作差作为紧组合系统的观测量.

(8)

式中：ρI为SINS计算所得载体和第j颗卫星间伪距；ρG为GNSS所得载体和第j颗卫星间伪距，

ρG=ρ+δtu+vρ,

(9)

式中：vρ为伪距的量测噪声.

理想伪距ρ与ρI可由下式计算得到

(10)

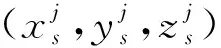
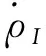
(11)

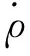
2.4 无迹卡尔曼滤波器

为了避免非线性系统的线性化误差， 获取更加精确的系统状态量均值与协方差估计[11]， 本文选用UKF算法对紧组合系统的数据进行融合处理. 通过采集的一组近似高斯分布的采样点对系统状态均值与误差协方差进行更新. 每次进行更新时， 采样点会随非线性状态方程进行传递并会随量测方程进行变换， 从而避免了非线性系统的线性化误差， 保证了状态估计精度， 具有较好的鲁棒性[12-14].

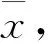
(13)

i=1,2,…,n,

(14)

i=n+1,n+2,…,L,

(15)

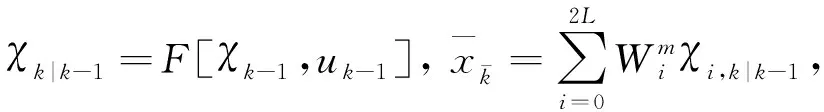
(16)

(17)

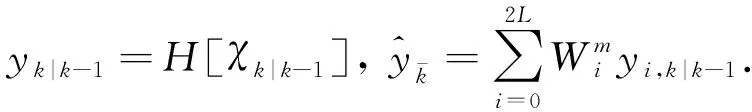
(18)

量测更新为

(19)

(20)

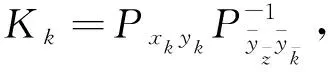
(21)

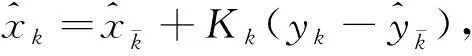
(22)

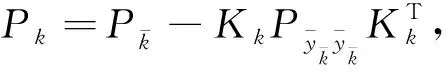
(23)

式中：Rv为系统噪声方差；Rn为观测噪声方差.

3 系统试验与分析

为了验证紧组合系统的总体性能， 对样机进行了车载试验. 图 3 为紧组合系统实物图.

图 3 紧组合系统实物图 Fig.3 Product photo of tight combinatio system

车载试验时， 将系统样机固定在一块金属板上置于汽车内， 将GNSS天线固定在样机上方的汽车顶部， 并忽略GNSS天线和样机之间的杆臂误差. 跑车试验于中北大学南门外新兰路进行， 跑车行驶路线为环形， 初始对准后， 行驶时间约为 450 s. 系统IMU模块的数据更新频率为100 Hz， GNSS的数据更新频率为 1 Hz， 实验过程中卫星信号良好， 可见星有7颗北斗与8颗GPS卫星， 最后对试验结果进行处理与分析， 得到紧组合与松组合导航系统的速度误差和位置误差对比.

ΔvE, ΔvN, ΔvU分别为车辆在东北天向速度误差， ΔPE, ΔPN, ΔPU分别为车辆在东北天向位置误差. 图 4 和图 5 分别表示GNSS卫星信号受到干扰失锁下紧组合和松组合算法的速度和位置误差的对比图.

图 4 卫星失锁下速度误差对比图Fig.4 Comparison of speed errors under satellite lock less

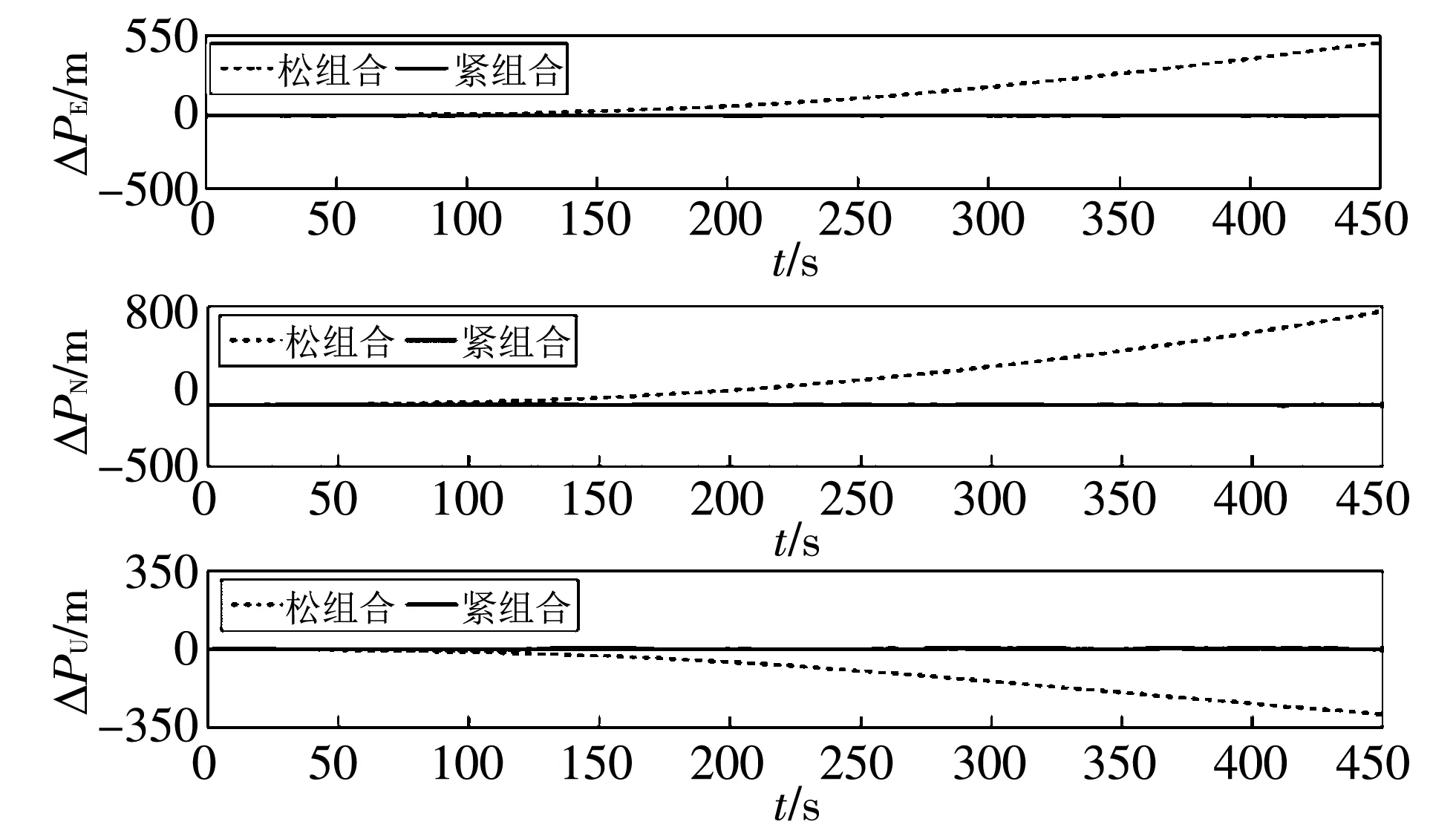
图 5 卫星失锁下位置误差对比图Fig.5 Comparison of position errors under satellite lock loss

对紧组合和松组合算法导航结果进行对比， 在0～100 s内， 可见卫星数大于4颗， 如图 4 和图 5 所示， 紧组合的速度误差和位置误差比松组合略小， 精度略高. 在100～300 s内， 选用3颗卫星进行数据融合， 此时可见卫星数小于4颗， SINS/GNSS松组合不能正常运行， 只能通过纯SINS解算进行定位. 松组合在GNSS信号受到干扰失锁200 s后， 东向、 北向和天向的速度误差分别达到了7.01， 6.71和4.90 m/s； 由于只能通过SINS解算进行定位， 在GNSS信号受到干扰失锁200 s后， 东向、 北向和天向的位置误差分别达到了196.4， 311.9和144.3 m. 由于捷联惯导导航误差会随时间进行累积， 因而发散速度特别快， 松组合系统的稳定性特别差. 而紧组合在可见卫星数目少于4颗时依然能够利用3颗卫星的数据进行数据融合， 并且速度误差和位置误差仍可以保持在一定的误差范围内.

图 6 和图 7 分别表示紧组合与松组合系统分别解算得到的东北天向速度与位置误差对比图.

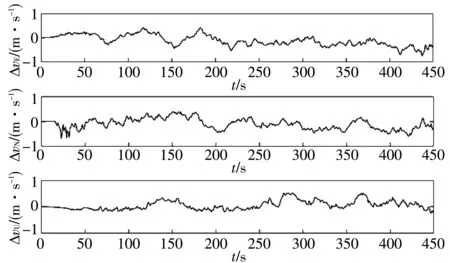
图 6 紧组合东北天向的速度误差图Fig.6 Velocity error diagram of tigh combination in east, north and sky directions

图 7 紧组合东北天向的位置误差图Fig.7 Position error diagram of tigh combination in east,north and sky directions

在0～100 s内， 可见卫星数大于4颗， 在100～300 s内， 选用3颗卫星信号进行数据融合. 如图 6 所示， 紧组合导航算法的速度误差小于1 m/s， 紧组合导航算法的东向、 北向和天向的速度误差的极值分别达到0.75， 0.69和0.52 m/s； 如图 7 所示， 紧组合算法的位置误差在5 m内， 紧组合算法的东向、 北向和天向的位置误差的极值分别达到3.11， 4.69和2.87 m.

试验结果表明， 所设计的基于ARM的SINS/GNSS紧组合导航系统， 与松组合算法相比具有更高的精度和稳定性， 在GNSS信号受到干扰失锁， 可见卫星数目少于4颗时仍能辅助SINS进行数据融合完成导航定位， 在一段时间里具有比较高的精度.

4 结 论

针对GNSS信号受到干扰失锁， 导致可见卫星数目少于4颗时SINS/GNSS松组合系统无法正常运行问题， 设计了基于ARM的SINS/GNSS紧组合导航系统， 建立了紧组合系统非线性模型， 并搭建了硬件系统， 采用UKF算法对紧组合数据进行融合. 测试结果表明， 设计的紧组合系统有着比松组合系统更高的导航精度与稳定性， 在GNSS信号受到干扰失锁时， 紧组合系统在短期内仍可保持较高的导航精度.