封装对高量程加速度计响应特性影响的分析

李 飞， 石云波， 赵永祺， 赵思晗， 张 婕， 米振国

(中北大学 电子测试技术重点实验室， 山西 太原 030051)

0 引 言

高量程加速度传感器主要应用在侵彻、 冲击、 爆炸等恶劣环境中， 因此保证传感器能在这些环境中正常工作至关重要[1-2]. 加速度传感器封装的主要作用是为芯片提供工作环境， 实现芯片对外的互连， 使传感器响应信号可以及时地输出， 同时保护器件， 提高其使用寿命， 因此封装对高量程微机械加速度计的应用具有重要意义[3]. Zarnik等[4]研究分析了贴片胶对传感器芯片热应力的影响， 蒋玉齐[5]研究了灌封胶弹性模量和密度对传感器输出性能的影响， Zhou等[6]研究了贴片胶对传感器零偏的影响. 现有研究主要集中在贴片胶和灌封胶的性能参数对高量程加速度传感器的输出响应特性的影响， 而对于封装管壳尺寸参数和灌封胶用量影响传感器响应特性的研究工作相对较少. 高量程加速度传感器应用环境特殊， 在其工作过程中， 冲击信号往往伴随着不同幅值以及频率加速度信号的叠加， 高频信号的输入难以避免. 传感器输出响应曲线中高频谐波的减少， 意味着传感器降低了对过载信号中耦合高频信号的响应和传感器动态线性度的改善[7]. 外加动态载荷中包含的与系统固有频率相近的频率信号， 会影响传感器输出特性甚至损坏器件结构. 以某口径火炮为例， 弹丸出膛时的加速度曲线中往往伴随着大量的高频谐波信号， 如果弹载传感器的固有频率过低， 实际的加速度信号会湮没在弹体振动的高频谐波中， 对后续加速度信号的处理以及测试加速度值的精度会造成很大的影响[8]. 为使传感器在这种情况下测得准确的加速度信号， 减少输出信号中的高频谐波， 有效的方法是提高传感器封装体的固有频率[9]， 因此如何提高传感器封装体固有频率， 减少响应曲线的高频谐波， 从而减小对传感器输出响应特性的影响， 对提高传感器的可靠性具有十分重要的意义.

1 理论模型建立

针对实验室自研的高量程加速度传感器[10]， 建立传感器封装体模型， 如图 1 所示.

模型中包括不锈钢壳体、 灌封胶、 贴片胶和玻璃-硅-玻璃三层键合传感器芯片， 传感器的敏感轴向为z轴方向. 封装完成的传感器在其频率响应曲线上存在多个谐振峰值， 其工作频带往往取决于封装体固有频率的下限. 提高封装体的固有频率能够减小传感器的测试误差， 在瞬态的冲击测试过程中可获得更高的测试精度[11]. 为研究封装体的固有频率与封装壳体盖板的关系， 根据传感器封装体模型建立了其封装盖板等效模型. 在封装体中， 盖板四边与管壳连接、 固定， 中间悬空， 因此可以将其看作一个四边固支的薄板模型. 针对薄板模型， 壳体内腔的宽度a作为薄板边长， 盖板厚度h作为薄板厚度， 等效模型如图 2 所示， 坐标原点位置在正方形薄板中心， 薄板的弯曲刚度D可以表示为

(1)

式中：E为薄板的弹性模量；μ为薄板的泊松比. 四边固支的正方形薄板边界条件为[12]

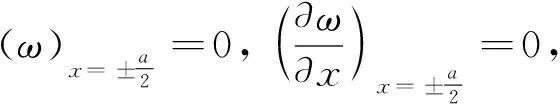
(2)

(3)

根据边界条件， 薄板的振型函数为

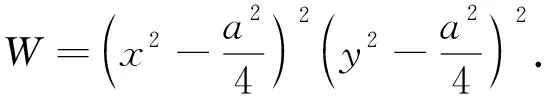
(4)

采用能量法可求解薄板的固有频率， 当薄板处于平衡位置最远处时， 动能为零[13]， 势能最大为

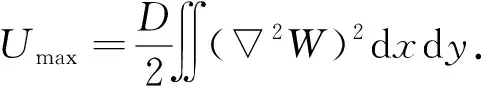
(5)

当薄板经过平衡位置处时， 势能为零， 动能最大为

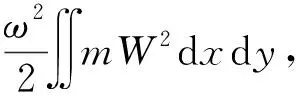
(6)

式中：m为薄板质量. 根据能量守恒定律可以得到

Umax=Kmax，

(7)

解得薄板结构的固有角频率为

(8)

从而求得其固有频率为

(9)

将式(1)代入式(9)中可以得到

(10)

式中：ρ为薄板材料密度. 由式(10)可以看出， 薄板的固有频率与其厚度成正比， 与薄板边长的三次方成反比.

图 2 封装盖板等效模型示意图Fig.2 Schematic of package cover equivalent model

2 有限元分析

为验证封装壳体内腔宽度、 管壳盖板尺寸对封装体和等效模型固有频率的影响， 通过有限元仿真分析不同宽度内腔和不同厚度盖板下封装体和其等效模型的固有频率.

2.1 封装壳体内腔宽度影响分析

根据传感芯片尺寸， 设计的封装壳体内腔高度为2.5 mm， 盖板厚度为0.5 mm， 内腔的最小尺寸设计为4 mm， 通过改变封装壳体内腔宽度， 保持其它结构参数不变， 得到仿真结果如图 3 所示.

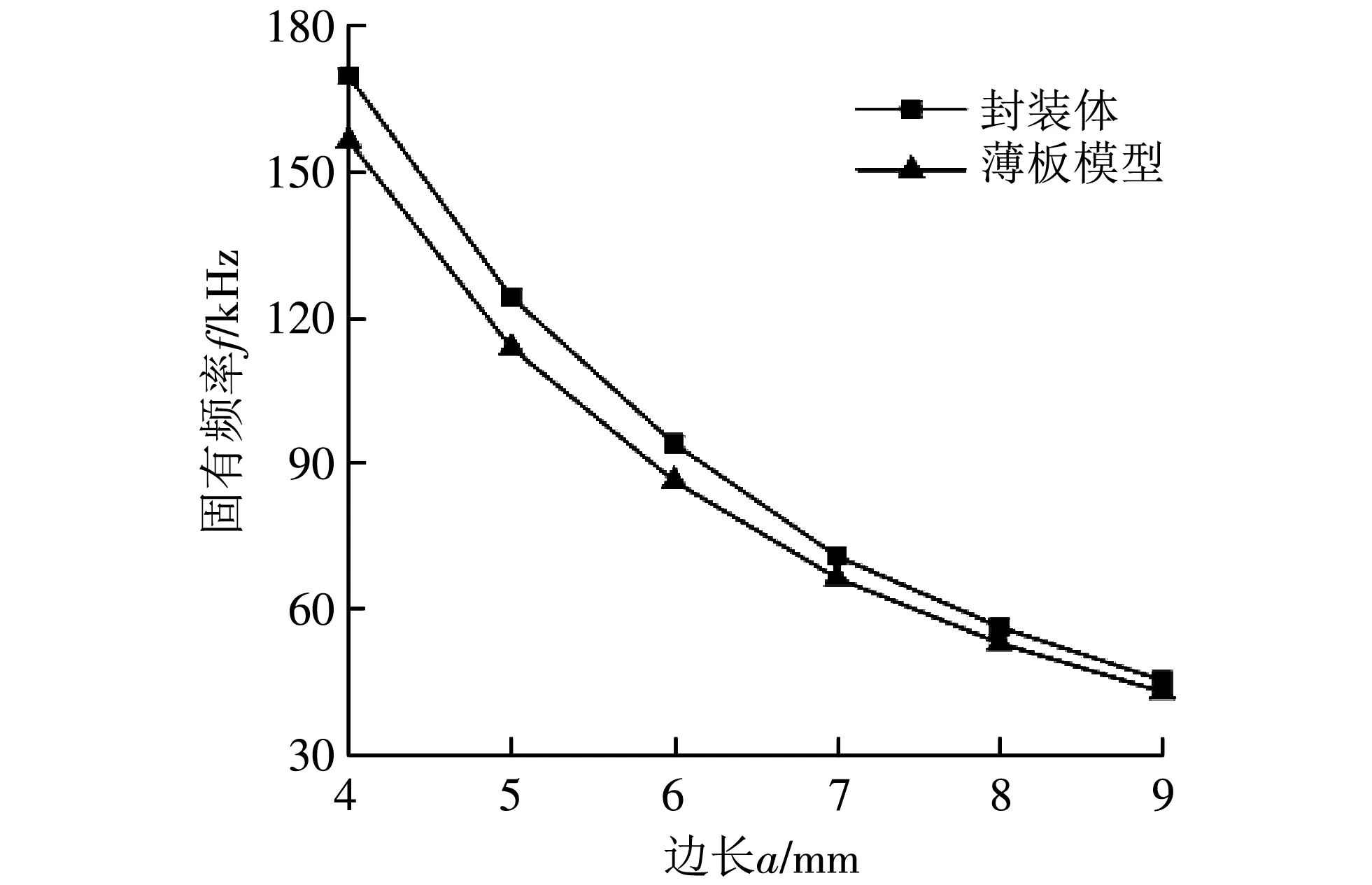
图 3 封装体与薄板模型固有频率随内腔尺寸变化规律Fig.3 Natural frequency of packaging body and cover plate model varies with cavity size of packaging shell

当封装壳体内腔长度和薄板边长相等时， 封装体与薄板模型的固有频率基本相等， 两者的固有频率随边长的减小而迅速增大， 有效地提高了整体一阶模态的固有频率， 满足式(10)中的函数关系. 同时可以观察到薄板模型的固有频率略低于封装体， 当内腔尺寸为4 mm时， 两者差异最大， 频率差值为3.33 kHz .

2.2 盖板厚度影响分析

不同盖板厚度的封装体及等效模型的一阶固有频率如图 4 所示. 随着盖板厚度的增加， 封装体和等效模型的固有频率逐渐增加. 盖板厚度在0.5～0.8 mm之间时， 封装体与等效模型的一阶模态固有频率的最大差值为2.326 kHz. 当盖板厚度大于0.8 mm时， 两者之间的差值逐渐增加. 通过模态振型分析可知， 造成这一现象的主要原因为随着盖板厚度增加至大于0.8 mm 时， 封装体的一阶模态振型由盖板的单一振动变成盖板和管壳壁的同时振动， 此时， 薄板模型的四边固支条件不再成立， 但增加盖板的厚度仍然可以有效增加封装体的固有频率.

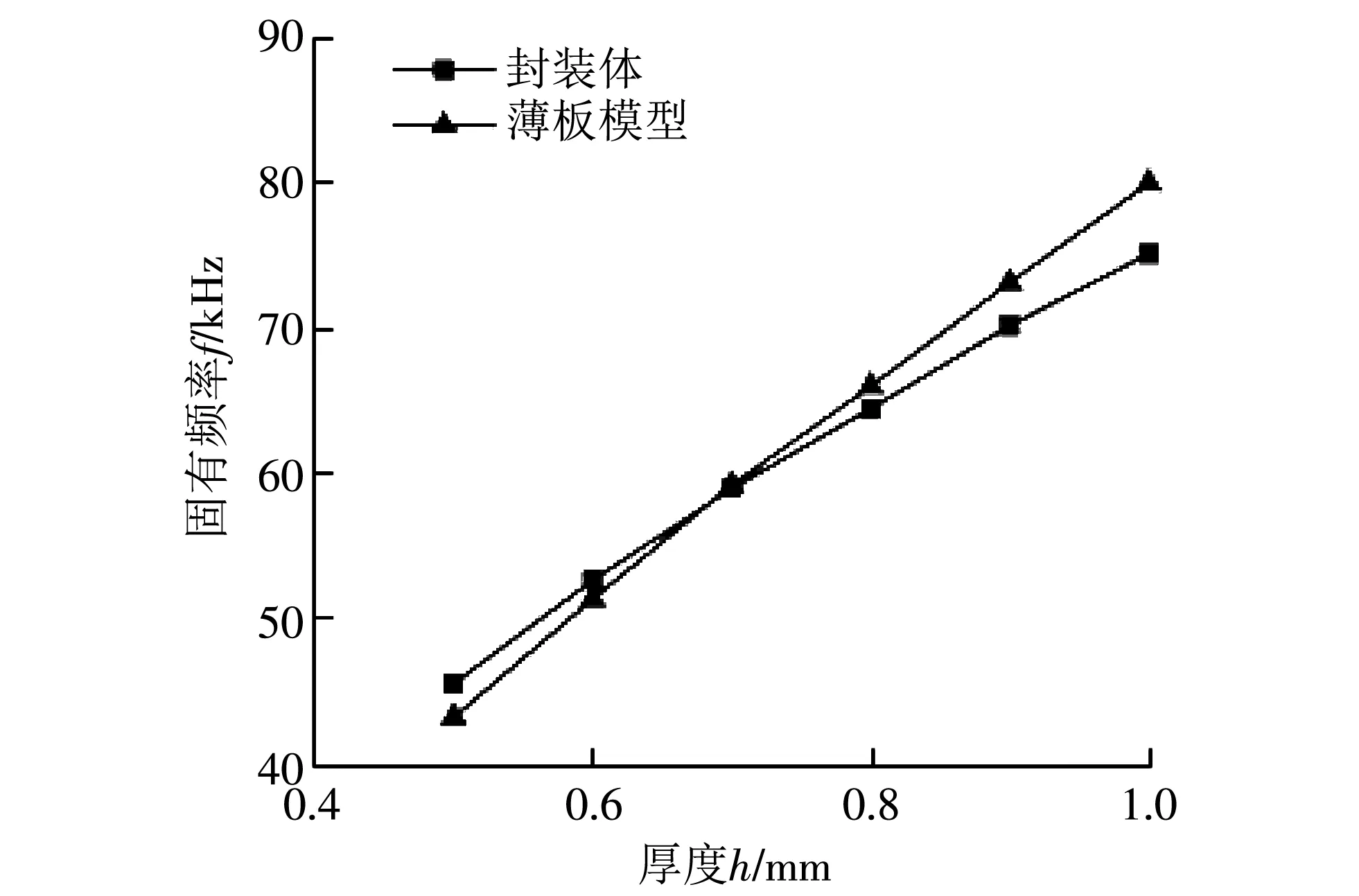
图 4 封装体与薄板模型固有频率随盖板厚度变化规律Fig.4 Natural frequency of packaging body and cover plate model varies with the thickness of cover plate

3 灌封对固有频率影响分析

3.1 封装体材料参数

通过灌封胶灌封可以实现对传感器器件的保护， 提高传感器封装体的固有频率. 为保护芯片， 选用的灌封胶弹性模量应大于4 GPa[14]. 灌封时不同用量的灌封胶会导致不同的封装效果. 因此， 分析灌封胶的用量对传感器封装体性能的影响， 有助于优化现有封装工艺. 使用有限元仿真软件， 对不同用胶量的封装体进行模态分析， 得出了不同用胶量对传感器封装体固有频率的影响. 在使用的封装壳体内腔尺寸和芯片结构尺寸一定时， 可以用灌封胶的厚度衡量灌封胶的用量. 封装体各材料的参数如表 1 所示.

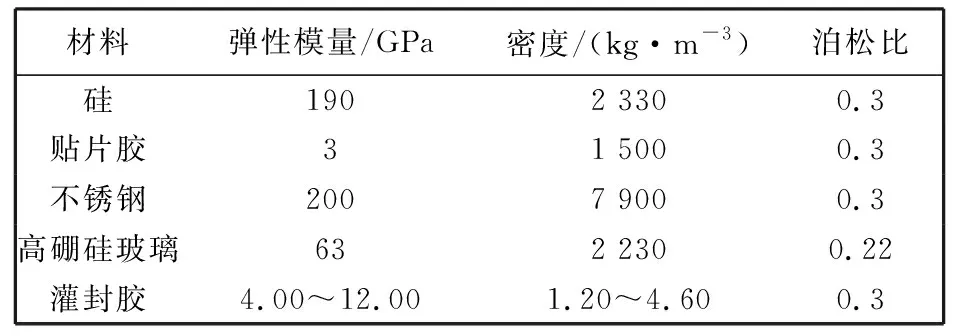
表 1 传感器封装体材料参数

3.2 仿真结果分析

传感器的封装体中贴片胶和芯片的总厚度约为0.8 mm， 为使灌封胶对芯片起到保护作用， 仿真中灌封胶厚度d设定在0.8～2.5 mm范围内. 仿真时对封装壳体底部进行固定约束， 通过改变模型中灌封胶的厚度， 对模型进行模态分析， 仿真中对芯片采取底面固定约束， 仿真结果如图 5 所示. 单独对芯片进行模态仿真得到的各阶模态频率值如表 2 所示. 通过对比发现， 封装体模态频率远小于芯片的模态频率， 因此封装体的模态频率决定了传感器的工作频率上限.

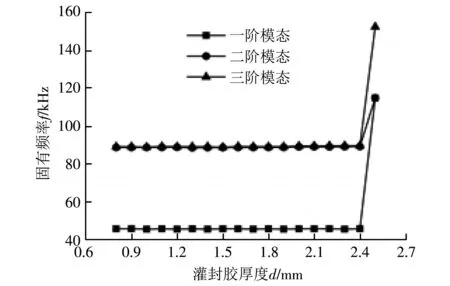
图 5 灌封胶用量对封装体固有频率的影响Fig.5 Effect of the amount of potting compound on the natural frequency of packaging body

表 2 芯片模态频率

Tab.2 Chip modal frequency

模态一阶模态二阶模态三阶模态频率/kHz332.9616.67618.77

从图 5 中可知， 在灌封胶未灌满封装壳体内腔时， 灌封胶的用量对传感器封装体的前三阶模态固有频率基本无影响， 其前六阶模态如图 6 所示， 其中一阶模态的振型表现为传感芯片敏感轴向(z方向)的振动.

灌封胶灌满封装壳体内腔时， 封装体前六阶模态如图 7 所示， 封装体的固有频率显著提高， 其中一阶模态的频率从45 kHz提高到114 kHz， 二阶模态的频率从89 kHz提高到115 kHz， 三阶模态的振型表现为传感芯片敏感轴向(z方向)的振动， 模态频率从未完全灌封的45 kHz提高到了150 kHz.

图 6 灌封胶未灌满封装壳体内腔时封装体模态Fig.6 The modal of the package body for the case of incompletely filled in the cavity of packaging by potting compound

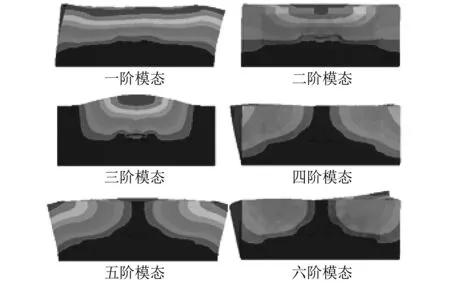
图 7 灌封胶灌满封装壳体内腔时封装体模态Fig.7 The modal of the package body for the case of completely filled in the cavity of packaging by potting compound

从图 6 和图 7 中可知， 灌封胶未灌满封装壳体内腔时， 封装体模态振型均表现为封装壳体盖板的振动； 而灌封胶灌满封装壳体内腔时， 盖板的振动被灌封胶制约， 传感器封装体的一阶模态振型发生了变化， 不再是盖板的弯曲振动， 而变成了封装体盖板、 灌封胶和管壳壁的整体振动. 相比于灌封胶未灌满封装壳体内腔的条件， 其固有频率明显提高. 因此， 对传感器管壳腔体进行完全灌封， 能有效提高传感器封装体的固有频率. 由于传感器封装体固有频率的下限决定了传感器工作频率的上限， 因此对传感器管壳腔体进行完全灌封， 可有效拓宽传感器的工作频带， 从而改善传感器的输出响应特性.

4 试验测试

为验证上述仿真结论， 对自研的压阻式高量程加速度传感器进行封装和性能测试， 封装后的传感器如图 8 所示. 测试所使用的马歇特落锤测试装置主要包括锤体、 电压放大器以及示波器. 对不同内径封装壳体的传感器、 不同厚度盖板的传感器和不同灌封量的传感器逐一进行测试.

图 8 封装后的传感器实物图Fig.8 The packaged sensor photograph

通过对管壳内径为6 mm和9 mm的传感器进行封装测试， 得到的传感器响应曲线如图 9 所示， 图 9(a)和图9(b)分别为管壳内径为9 mm和6 mm时传感器的输出响应曲线. 通过对比可知， 减小封装壳体内径可以有效减少传感器响应曲线的高频谐波. 同时， 本文对不同厚度封装盖板的传感器进行了冲击测试， 得到的响应曲线如图 10 所示， 图10(a)和图10(b)分别为盖板厚度为 0.5 mm 和 0.8 mm 时传感器的输出响应曲线. 可以观察到通过增加封装壳体的盖板厚度， 传感器输出曲线中的高频谐波可以得到有效抑制. 使用管壳内径为6 mm， 在灌封胶厚度为0.8 mm和完全灌封情况下， 对传感器进行冲击测试得到的响应曲线如图 11 所示. 试验结果表明， 在冲击测试过程中， 完全灌封的传感器与未完全灌封的传感器相比， 传感器响应曲线的高频谐波得到大幅衰减， 有效避免了共振现象. 通过测试验证了减小封装管壳内径、 增加盖板厚度和完全灌封封装管壳内腔这3种方法， 可以有效减小传感器响应曲线中的高频谐波， 从而改善传感器的输出响应特性.

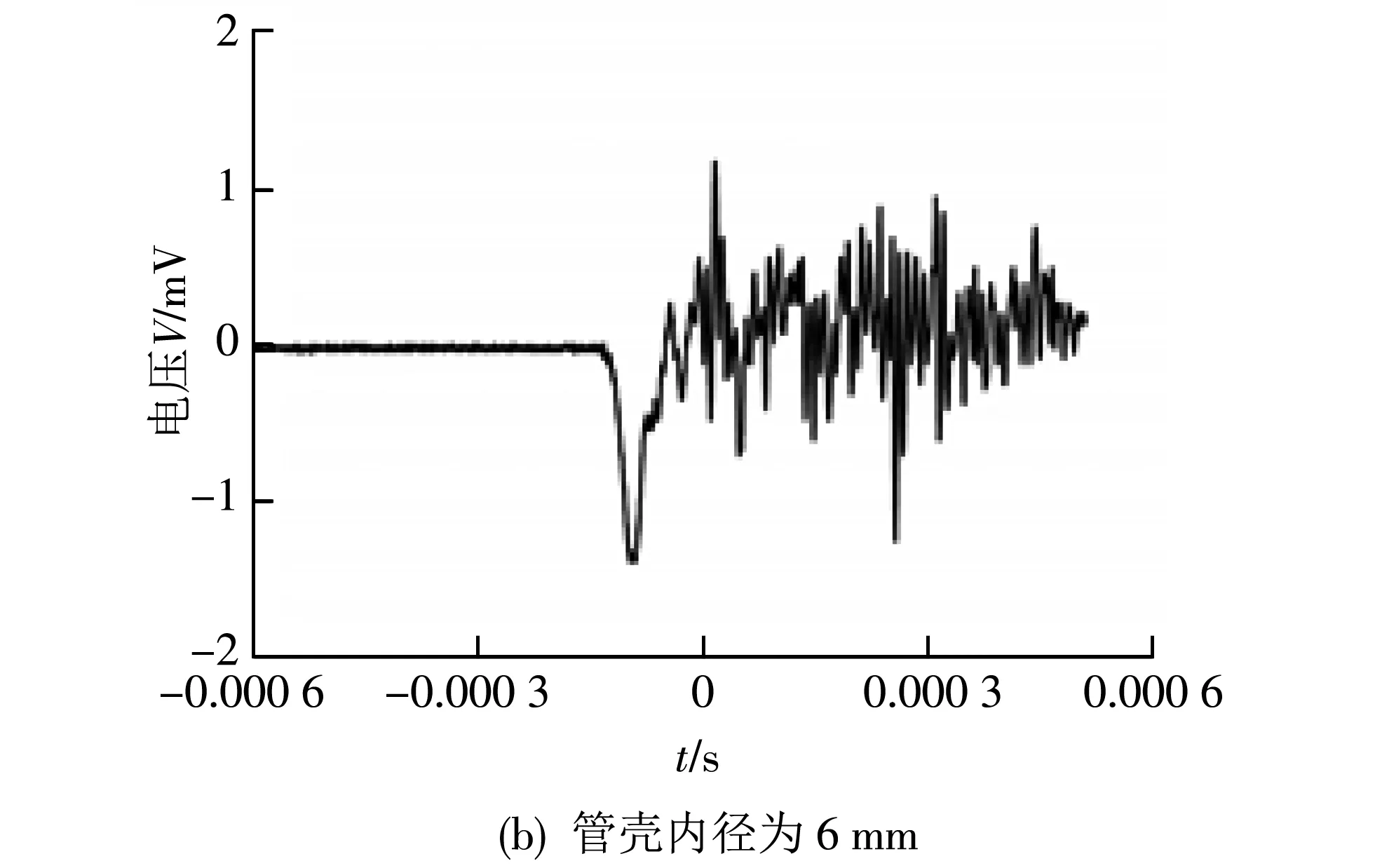
图 9 不同管壳内径的传感器输出响应曲线Fig.9 The output response curves of acceleration sensors with different inner diameters of packaging shell

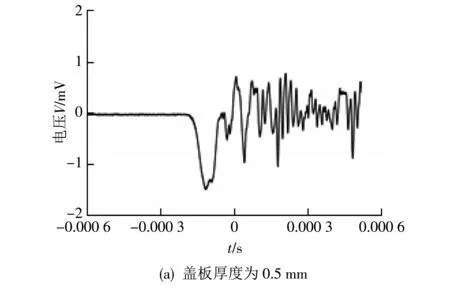
图 10 不同盖板厚度的传感器输出响应曲线Fig.10 The output response curves of acceleration sensors with different thickness of cover plate of packaging shell

图 11 不同灌封量的传感器输出响应曲线Fig.11 The output response curves of acceleration sensors with different dosage of potting compound

5 结 论

本文基于自研高量程加速度传感器， 通过理论计算和有限元分析方法， 研究了传感器封装管壳内径、 盖板厚度、 灌封胶用量对传感器封装体固有频率的影响， 并开展了试验验证. 结果表明减小管壳内径、 增加盖板厚度和完全灌封有利于提高传感器封装体固有频率， 从而改进传感器响应特性.