巧用单位圆求解三角函数问题

广东省中山市中山纪念中学

三角函数的定义来自于单位圆，利用单位圆的定义法来研究三角函数，以及单位圆中的三角函数线与单位圆的定义的联系，使我们能方便地采用数形结合的思想讨论三角函数的性质，如经典的不等式：当时，sinα＜α＜tanα以及两角差的余弦公式的证明都用到了单位圆.在三角函数中会经常遇到一些涉及已知三角函数值求角，求三角函数值，比较三角函数值的大小及其证明的问题，有时我们可以利用单位圆数形结合的思想去思考、分析和判断，往往能达到出奇制胜的效果，下面举例说明.

一、巧用单位圆求值

例1已知2 sinα+cosα=则tanα=___.

解点A(cosα,sinα)可看作直线与单位圆x2+y2=1的交点，由于原点O到直线l的距离为故直线l与圆相切.从而

变式若方程sinx+2 cosx=的两根为α,β，则tanα·tanβ=______.

解点A(cosx,sinx)可看作直线l:与单位圆x2+y2=1的交点，由于原点O到直线l的距离为故直线l与圆相交.由题意两交点分别为P(cosα,sinα),Q(cosβ,sinβ)，结合距离可知此时OP⊥OQ.于是tanα·tanβ=kOP·kOQ=-1.

图1

评注借助单位圆，我们还可以分别求出tanα,tanβ，如图1，作OM⊥l于点M，记直线OM的倾斜角为θ，则于是

例2 已知sinα+sinβ+sinγ=0，cosα+cosβ+cosγ=0，求cos2α+cos2β+cos2γ的值.

解点A(cosα,sinα)、B(cosβ,sinβ)、C(cosγ,sinγ)均在单位圆上，由条件可知ΔABC的重心坐标

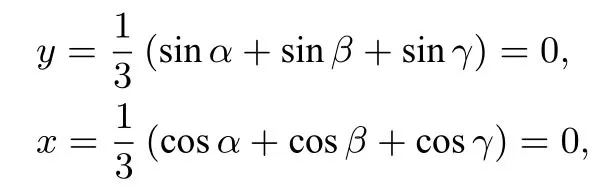
而其外心也为原点，即重心与外心重合，故ΔABC为正三角形.于是

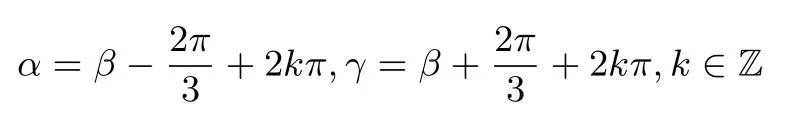
从而

二、巧用单位圆证明三角恒等式

例3 已知求证：

证明由已知条件可知点在x2+y2=1上，记则x0cosβ+y0sinβ=1，又单位圆x2+y2=1在点A处的切线l的方程为x0x+y0y=1，可见它过点B(cosβ,sinβ)，故A,B两点重合，于是因为cos2α=cos2β，且sin2α=sin2β，所以

例4已知锐角α,β为方程acosx+bsinx=c(a0,c0)的两不等实根，求证：

图2

证明由已知，点M(cosα,sinα)，N(cosβ,sinβ)(α＜β)可看作直线l:ax+by-c=0与单位圆x2+y2=1的两个交点，如图2，过原点O作OP⊥MN于点P，原点O到直线l的距离在RtΔOPN中，则于是

三、巧用单位圆求三角函数的最值

例5求函数的值域.

解令P(cosx,sinx),Q(2,0)，则如图3，当过Q点的直线与单位圆相切时的斜率便是函数的最值，由几何知识，易求得过Q的两切线的斜率分别为结合图形可知，函数的值域是

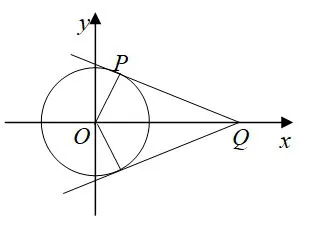
图3

例6(2018年高考全国I卷第16题)求函数f(x)=2 sinx+sin 2x的最值.

图4

解显然f(x)为奇函数，故只需求出f(x)的最大值即可.又f(x)=2 sinx+sin 2x=2 sinx(1+cosx)，记sinx=m,cosx=n，f(x)=t，则于是原题等价于在单位圆m2+n2=1条件下求目标函数的最大值，它是由反比例函数变换过来的，如图4，当它们的图像在第一象限相切时，t最大，设切点为(m0,n0)，则有消去n0和t得：化简得：因为m0＞0，从而此时即利用f(x)为奇函数知

点评此题作为2018年高考全国卷I的填空压轴题，一般是利用导数求最值.这里我们利用单位圆求解，此法很容易推广到如下的一般情形：求函数f(x)= sinx(a+cosx)的最大值t.

(1)当a≥0时，它由下面的方程组确定：化简得1-a2=0，此时m0=最大值为

(2)当a＜0时，它由下面的方程组确定：化简得a2=0，此时m0=最大值为

例7求函数的最大值.

解

记sinx=m,cosx=n，f(x)=t，则

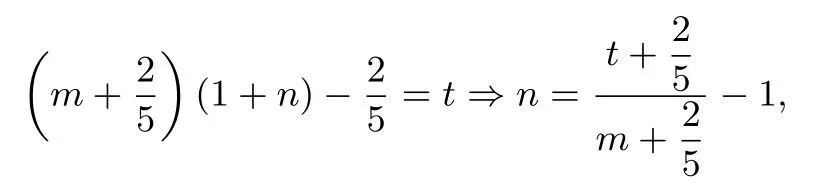
于是原题等价于在单位圆m2+n2=1下求目标函数的最大值，它是由反比例函数变换过来的，当它们的图像在第一象限相切时，t最大，设切点为(m0,n0)，则有消去n0和t得：化简得：100m30+40m20-71m0-20=0，即(5m0-4)20m20+24m0+5=0，因为0＜m0≤1，从而此时即

评注利用单位圆思想，此法很容易推广到下面的一般情形：函数的最大值为t，这里只讨论a≥0,b≥0的情形.它由下面的方程组确定：化简得此时

从以上问题我们看到，利用单位圆求解三角函数问题有时会给我们带来意想不到的效果，在平时的教学中，我们要引领学生从不同的角度去观察问题，这样不仅能拓展学生的思维，还能取得很好的教学效果.