关于三角函数线性组合最值问题的解析

陕西省西安市第三中学

数学源于生活，而生活中的实际问题又可以体现数学的价值，数学的价值在于对问题的探究和进一步研究，本文是从一道模考试题谈起，经过解法研究、推广、变式一系列的活动使问题的价值逐步提升，将“一题多变”发挥极致，只有不断研究试题，才能实现由“必然王国”向“自由王国”的转变，才会更精彩，这正好也是数学的价值所在.

题目(2019年江苏无锡模拟考试第14题)已知在锐角三角形ΔABC中，2sin2A+sin2B=2sin2C，则的最小值为____.就变成了C′:x2+y2=1，即椭圆C上的点

解法1因为2sin2A+sin2B=2sin2C，所以2a2+b2=2c2，即b2=2(c2-a2).又因为c2=a2+b2-2abcosC，所以b2=2(b2-2abcosC)，即b=4acosC.由正弦定理得sinB=4 sinAcosC，所以sin(A+C)= 4 sinAcosC.化简得tanC=3 tanA，又因为A+B+C=π，所以

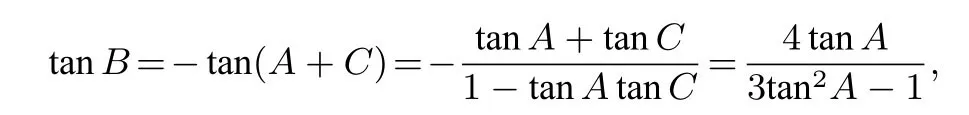
故

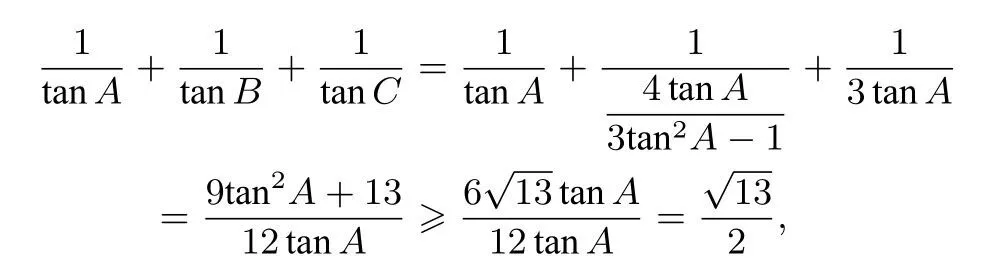
解法2作BD⊥AC于点D，设BD=h，则c2=h2+AD2,a2=h2+CD2，所以

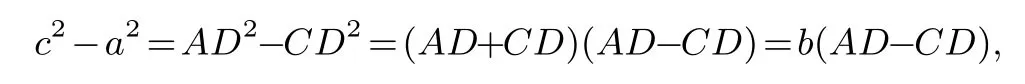
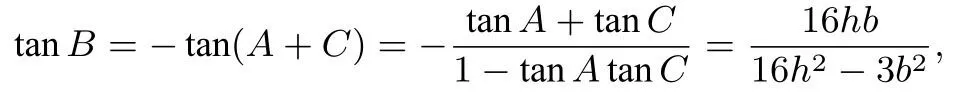
所以

推广1已知在ΔABC中，ksin2A+sin2B=ksin2C,(k0)，则的最小值为

证明作BD⊥AC于点D，设BD=h，则c2=h2+AD2,a2=h2+CD2,所以c2-a2=AD2-CD2=(AD+CD)(AD-CD)=b(AD-CD),所以又因为AD+CD=b，所以又因为ksin2A+sin2B=ksin2C，所以ka2+b2=kc2，即c2-a2=所以

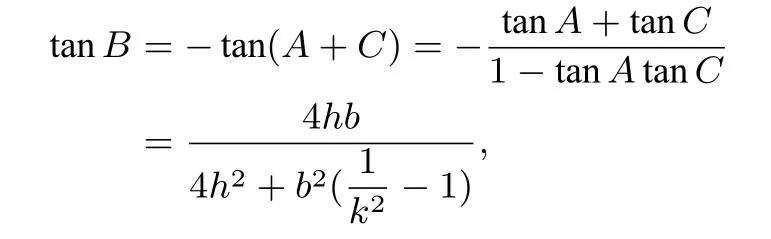
所以

当且仅当h=时，等号成立，故的最小值

推广2已知在ΔABC中ksin2A+sin2B=ksin2C,则的最小值为

证明作BD⊥AC于点D，设BD=h，则c2=h2+AD2,a2=h2+CD2，所以c2-a2=AD2-CD2=(AD+CD)(AD-CD)=b(AD-CD)所以又因为AD+CD=b，所以又因为ksin2A+sin2B=ksin2C，所以ka2+b2=kc2，即c2-a2=所以

所以

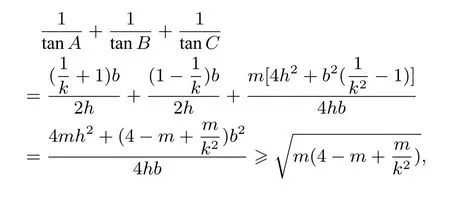
变式1在锐角三角形ΔABC中，角A,B,C的对边分别是a,b,c，若sin2A+sin2C=则

证明因为所以又因为A+B+C=π，所以

推广3在三角形ΔABC中，角A,B,C的对边分别是a,b,c，若sin2A+sin2C=λsin2B(其中(λ+1)sin2B,2sin2C(λ+1)sin2B)，则

证明因为sin2A+sin2C=λsin2B，所以a2+c2=λb2，又因为A+B+C=π，所以

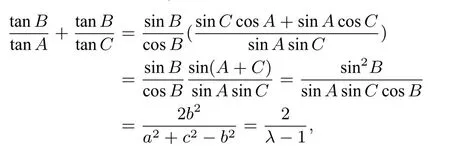
推广4设点B是圆x2+y2=r2(r＞0)上一点，若(其中m＞0,m1).若ΔABC为斜三角形，则

证明设当x＞0,y＞0时，有所以

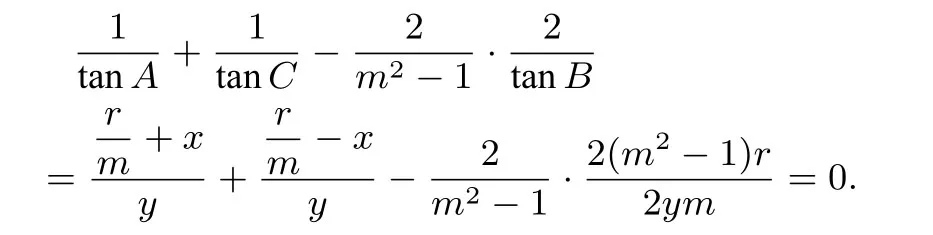
其它情形同理可证.

变式2已知在三角形ΔABC中，2 sinA+sinB=2 sinC，求的最小值.

解法1因为2 sinA+sinB=2 sinC，所以2 sinA+sinB=2 sin(A+B)，所以2 sinA(cosB-1)= sinB(1-2 cosA)，即所以即所以所以

解法2因为2 sinA+sinB=2 sinC，所以b=2(c-a)，设b=4，则c-a=2，即|AB|-|BC|=2＜4，所以，点B的轨迹为双曲线在第一象限的部分，由焦半径公式得

推广5已知在三角形ΔABC中，ksinA+sinB=ksinC,(k＞1)，则的最小值为

解因为ksinA+sinB=ksinC，所以b=k(c-a)，设b=4，则因为k＞1，所以所以，点B的轨迹为双曲线在第一象限的部分，由焦半径公式得

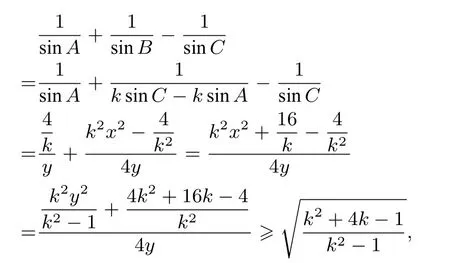
推广6已知在三角形ΔABC中，ksinA+sinB=ksinC,(k＞1,m＞0)，则的最小值为

解因为ksinA+sinB=ksinC，所以b=k(c-a)，设b=4，则因为k＞1，所以所以，点B的轨迹为双曲线在第一象限的部分，由焦半径公式得

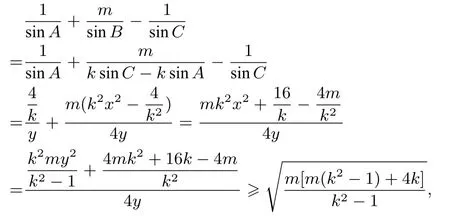
通过以上的思考过程，笔者感悟到对于任何试题的研究，需要平时的积累，通过用抽象、类比、和变式去研究数学问题，在平时教学中要多思、多想，多问为什么，这样数学会因思考而更加精彩，一道优秀的试题是要经过多思善想，这样才会有惊喜和收获，只有在学习中才可以提升数学品质和数学素养，既需要大胆的猜想和细心的求证，还需要坚定的意志和灵通的变通，所以说，只有多思、多想、多变，才会有创新，发现和收获.