高观点下透析“图形特殊化”的源与流*

西南大学附属中学校

一、缘起

在解决有的几何题目时，如果我们将图形做适当的变形，将其变得更为特殊和熟悉的图形，在不改变图形中的关键要素的前提下，会发现变形后题目的结果不会发生变化或者与原来的结果有显而易见的联系，进而，惊喜地发现原本“较为陌生、较为复杂、难以描述”的图形关系变得“较为熟悉、容易刻画、便于表达”起来，题目也就迎刃而解了，我们把这样的解题方法叫做“图形特殊化”.图形为什么可以特殊化?背后的原理又是什么?什么情况下可以特殊化?接下来，带着这样的问题，我们不妨从一道竞赛试题的妙解说起，然后站在高观点下从仿射变换的视角透析其背后的高等几何背景，同时基于通透的前提下结合笔者的教学经验，举例说明这种方法在初等几何解题中经常遇到的几种情形.

二、从解一道竞赛试题看“图形特殊化”的巧与妙

下面这道题是北京市中学生数学竞赛预赛的最后一个题目，主要考查学生认识图形、分析图形，综合运用所学知识解决图形中线段比例、三角形面积等相关问题的能力，考虑到是最后一个题，命题者故意做了一定的伪装，穿了几件衣服，显得较为新颖，有一定的难度.

例1(2019年北京市中学生数学竞赛预赛试题(高一)第二大题第8题)如图1，在ΔABC的边AB，BC上分别取点K，M，使得在线段KM上取点O，使得N为射线BO与AC的交点，AC=a，由点O到AC边的距离OD=d，则ΔKMN的面积为___

题目分析与解如图2，通过细致分析不难发现题目中图形关系的关键在于“点O分BN成的比和点N分AC成的比是确定的”，考虑到这是一道填空题，而“点O分BN成的比和点N分AC成的比”不会因为三角形形状的改变而改变，也就保证了图形中的三角形面积比例不会发生改变，只要保证“AC=a，OD=d”这个条件，就可以把三角形特殊化.

图1

图2

不妨让AB⊥AC，以AB,AC分别为x,y轴建立平面直角坐标系，则C(a,0)，设B(0,b)，由易得由易得再结合可求得这就求出了于是直线令y=0可得：这就求出了由于于是

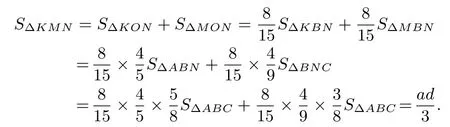
解法点评解法的精髓在于巧妙地利用了图形特殊化后“线段比例”不会改变、面积比也不改变这两个事实，将图形特殊化，变成直角三角形后更有利于坐标系的建立，从而将复杂的图形关系变为容易用坐标计算的图形关系，实现了小题小解、小题巧解.

三、透析“图形特殊化”背后的高等几何背景

我们在感叹“变得巧、解得妙”的同时，自然而然地会思考这样的问题：图形为什么可以特殊化?其背后的原理又是什么?什么情况下可以特殊化?其实，根据高等教育出版社出版的《高等几何》[1]，我们不妨先依次弄清下列问题.

(一)什么是透视仿射对应

定义1.1共线三点P1，P2，P的单比表示为(P1P2P)，定义其中P1P、P2P是有向线段的数量，称P1，P2为基点，P为分点.

定义1.2在一平面上设有直线a和a′，l为此平面上与a,a′均不平行的另一直线，通过直线a上各点A,B,C,···，分别作与l平行的直线，顺次交a′于A′,B′,C′,···，这样便得到直线a上点到a′上点的一个一一对应，称为透视仿射对应，如图3所示.

图3

类似地可以定义空间两平面间的透视仿射对应.显然，透视仿射对应有以下性质：

性质1.1透视仿射对应保持同素性.即透视仿射对应使点对应点，直线对应直线.

性质1.2透视仿射对应保持结合性，如图3所示，点A,B,C,···,在a上，通过透视仿射对应后，其对应点A′,B′,C′,···,在a′上.

性质1.3透视仿射对应保持共线三点的单比不变.如图3，由平行切割对应成比例容易知道，单比(ABC)=(A′B′C′).

性质1.4透视仿射对应保持两直线的平行性.

(二)什么是仿射对应与仿射变换

定义2.1设同一平面内有n条直线a1,a2,···,an.φ1,φ2,···,φn-1顺次表示a1到a2，a2到a3，···，an-1到an的透视仿射对应，经过这一串透视仿射对应，使a1上的点与an上的点建立了一一对应，这个对应称为a1到an的仿射对应φ(也叫仿射变换)，于是有：φ=φn-1°···°φ2°φ1.

类似地可以定义空间两平面之间的仿射变换.不难证明仿射对应(变换)满足以下性质：

性质1.1仿射对应保持同素性与结合性.

性质1.2仿射对应保持共线三点的单比不变.

性质1.3仿射对应保持两直线的平行性.

(三)什么是仿射坐标

如图4，设O-xy为平面内一笛卡尔坐标系(直角或斜角)，E(1,1)为单位点，平面内任一点P(x,y)都可以表示为其中Ex,Ey,Px,Py分别为过E,P所作y轴和x轴的平行线与x轴和y轴的交点.

图4

经过一个仿射变换(对应)，坐标系O-xy在同一平面(另一平面)内的对应图形为O′-x′y′，E,Ex,Ey,P,Px,Py的对应点顺次为E′,E′x,E′y,P′,P′x,P′y，在新坐标系O′-x′y′中，取E′(1,1)为单位点，对于这个坐标系中的点P′(x′,y′)，就有由于仿射变换保持单比不变，所以有x=x′，y=y′.

定义3.1笛卡尔坐标系在仿射变换(对应)下的像叫做仿射坐标系.(x′,y′)叫做点P′的仿射坐标，记为P′(x′,y′).

由此可见仿射坐标系是笛卡尔坐标系的推广，两坐标轴上的测量单位|O′E′|和|OE|不一定相等，而笛卡尔坐标系是仿射坐标系当两轴上的测量单位相等时的特殊情况.

(四)什么是仿射变换的代数表示

如图5，设仿射变换将坐标系O-e1e2变为O′-e′1e′2，点P变为P′.记P(x,y)，P′(x′,y′)，O′(x0,y0)，e1=(x1,y1)，e2=(x2,y2)，那么如何求点P′(x′,y′)在新坐标系中的坐标呢?

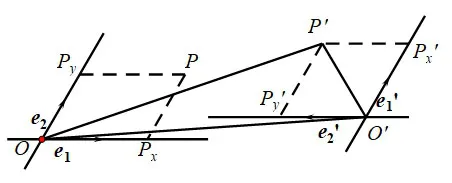
图5

考虑到仿射变换保持平行性和单比不变，故点P′在坐标系O′-e′1e′2下的坐标仍然为(x,y)，故只需在O-e1e2中找到P(x,y)与P′(x′,y′)的关系即可，由于所以

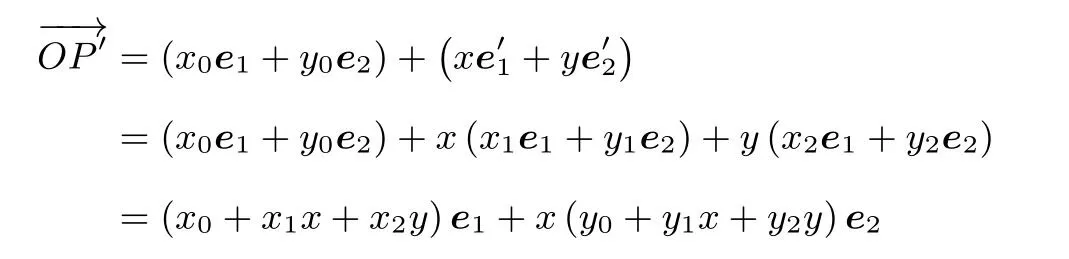
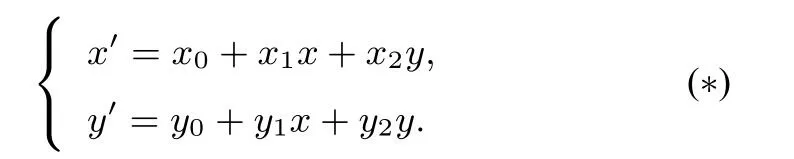
由于e′1与e′2不平行，所以有

由于式中有六个未知数，所以只要有不共线的三对点便可唯一确定一个仿射变换.

定义4.1平面上点之间的一个线性变换(∗)叫做仿射变换，其中

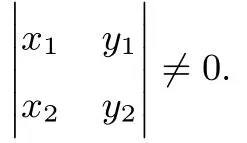
这就是仿射变换的代数表示，我们有必要了解以下几个特殊仿射变换的代数表示：

(1)正交变换如果(∗)式满足时，则称该仿射变换为正交变换.正交变换保任意两点之间的距离不变.

(2)位似变换如果(∗)式满足其中k0，则称该仿射变换为位似变换.位似变换中，唯一的不动点叫位似中心，k为位似比，位似变换保夹角不变和对应线段的比值不变.

(3)伸缩变换如果(∗)式满足其中λµ0，则称该仿射变换为伸缩变换.

(五)什么是仿射不变量

定义5.1图形经过任何仿射变换后都不变的性质(量)，称为图形的仿射不变量.

性质5.1经过仿射变换的直线，平行性不改变，相交性不改变，对曲线的切性不改变.

性质5.2两条平行线段之比是仿射不变量.

性质5.3两个三角形面积之比是仿射不变量，两个多变形面积之比是仿射不变量.

性质5.4在伸缩变换(其中λµ0)下，变换前后直线斜率比为

性质5.5在伸缩变换(其中λµ0)下，变换前后多边形面积比为

由前面概念产生过程看，性质5.1和5.2是显然成立的，由(∗)式大家不难证明性质5.3、5.4和5.5也是成立的，大家可以参考书[1].

(六)什么是“图形特殊化”的高等几何背景

结合前面的叙述可知，“图形特殊化”的本质是作了一个恰当的仿射变换，图形为什么可以特殊化呢?是因为仿射变换下存在仿射不变量.就像例1 那样，由于“两条平行线段之比”和“两个三角形面积之比”是仿射不变量，故将“图形特殊化”后答案不会发生变化!

四、例说“图形特殊化”的几何应用

下面回答最后一个问题，哪些情形适用“图形特殊化”，笔者结合实例，谈谈自己在平时教学中积累的几种情形.

(一)利用“图形特殊化”巧解斜率相关问题

结论1如图6，设椭圆斜率为kAB的直线l交椭圆C于A、B两点，AB中点为M，直线OM(O为坐标原点)的斜率为kOM，则有

图6

证明作伸缩变换φ:则椭圆C:就变成了C′:x2+y2=1，即椭圆C上的点A,B,M就变成了圆C′上的点A′,B′,M′，M是弦AB的中点，由于两条平行线段之比是仿射不变量，故M′也是A′B′的中点，若该变换将直线l(斜率为k)变换成直线l′(斜率为k′)，由性质必有又因为圆C′中k′AB·k′OM=-1，于是即证得

类似地，很容易得到以下两个结论；

结论2斜率为kl的直线l与椭圆1(a＞b＞0)相切于点A，点A与坐标原点O连线OA的斜率为kOA，则有

结论3设椭圆A、B两点关于坐标原点O对称，点P为椭圆上不同于A、B的任意一点，直线PA和PB的斜率存在且分别为kPA和kPB，则有

(二)利用“图形特殊化”巧解线段长度相关问题

例2(2017年沈阳四中期中考试题)如图7，在ΔABC中，点P是AB上一点，且Q是BC的中点，AQ与CP的交点为M，又则实数t的值为___.

图7

图8

解如图8，由于仿射变换保线段比例不变，不妨让BC⊥BA，且以BC,BA分别为x,y轴建立平面直角坐标系，同时设A(0,3)，设C(2,0)，由易得P(0,2)，又Q是BC的中点，Q(1,0)，易求得直线与直线的交点故

例3(2013年湖北数学竞赛预赛试题)设P(x0,y0)是椭圆内一定点(不在坐标轴上)，过点P的两条直线分别交椭圆于A,C和B,D，若AB//CD，过点P作与AB平行的直线交椭圆于E,F，求证：点P平分EF.

简证如图9，做仿射变换φ:由于仿射变换保持直线的平行性，四边形A′B′C′D′为等腰梯形，且A′B′中垂线过点P′和原点，由A′B′//E′F′，故点P′平分E′F′.

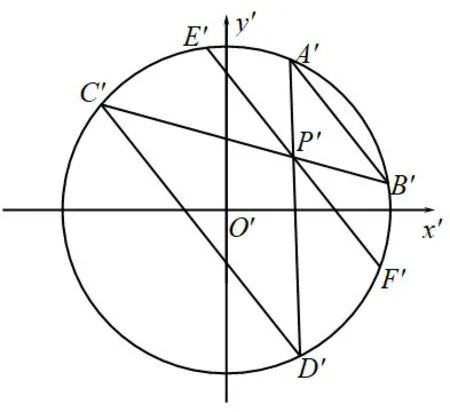
图9

图10

(三)利用“图形特殊化”巧解面积相关问题

例4(2019年高考全国II卷第21题)如图10，已知点A(-2,0)、B(2,0)，动点M(x,y)满足直线AM和BM的斜率之积为记M的轨迹为曲线C.

(2)过坐标原点的直线交C于P、Q两点，点P在第一象限，PE⊥x轴，垂足为E，连接QE并延长交C于点G.

(i)证明：ΔPGQ是直角三角形；(ii)求ΔPGQ面积的最大值.

解(2)作伸缩变换φ:则椭圆C:P,Q,G,E就变成了圆C′上的点P′,Q′,G′,E′.

(i)不妨设P′(m,n)，则，由于P′G′⊥Q′G′，故显然kP′Q′·kP′G′=所以kPQ·kPG=-1，即证：PQ⊥PG.

(ii)设∠Q′P′G′=α，由夹角公式

由于P′G′⊥Q′G′所以

于是SΔPGQ=

五、后记

“会当凌绝顶，一览众山小”.在克莱因看来：“基础数学的老师应该站在更高的视角(高等数学)来审视、理解初等数学问题，只有观点高了，事物才显得明了而简单”[2].而只要掌握了“图形特殊化”背后“仿射变换”这个高等几何背景，就会发现很多可以用它来解决的问题，同样很多看似巧妙的背后，往往隐藏着深刻的数学本质.