一类“不确定三角形”问题的求解策略

云南省高中数学张勇名师工作坊；云南省下关第一中学

解三角形作为高考重点考查内容之一，主要要求考生通过对任意三角形边角关系的探索，掌握正弦定理、余弦定理、三角形的面积公式等，并借助三角函数中的相关公式加以综合与运算，解决一些简单三角形的度量问题及一些与测量和计算有关的实际问题等.涉及解三角形与三角函数知识，大都运算量大、公式应用多，这就要求考生不仅要具有较高的运算能力、较强的应变能力和较好的记忆能力，还要善于分析与总结，形成解决此类问题的一般方法.

对于高中生而言，初中阶段就已经非常熟悉确定三角形的条件，即：边角边、角角边、边边边、角边角都可以唯一确定三角形，那么其解三角形问题只需简单的使用正、余弦定理即可解决，也被学生所熟练掌握.结合教学实际，从高考的能力立意来看，纵观2010至2019年全国新课标高考试题中“已知一角一边”的解三角形问题是高频考点，这是一类不确定三角形的求解问题，其往往结合三角函数、三角恒等变换、不等式等知识作为压轴题型进行综合考查，涉及最值、范围问题等，这类情况是简单的正余弦定理不能直接解决的，也是教学和高考中的重难点.作者结合教学实际和对高考试题的深入分析，总结得出了解三角形中“已知一角一边”问题的求解方法，并在此基础上提炼出了以下两个模型.

模型一 已知三角形的一角及其对边

如图，在ΔABC中，已知ΔABC的三个内角为A,B,C，其对应的三边为a,b,c，且A=60°，a=2(即已知三角形一角及其对边)，则根据三角形的边角关系就可得到以下三个隐含的解题条件：

其中R为ΔABC外接圆的半径(实现了边角的相互转换).

以上三个隐含的解题条件深刻揭示了解三角形中“已知一角及其对边”的本质就是：角的关系(内角和定理)、边角的关系(正余弦定理)，掌握住这个本质就可解决多种不同类型的问题，进而得到解决此类问题的系统方法.比如，在上述条件下可求：

(1)B+C；

(2)ΔABC外接圆的半径；

(3)sinB+sinC的取值范围(扩展到求t1sinB+t2sinC(t1t20)的最值)；

(4)b+c的取值范围(扩展到求λb+µc(λµ0)的最值)；

(5)ΔABC周长的最大值(即求a+b+c的最大值)；

(6)ΔABC面积的最大值.

结合“已知三角形一角及其对边”的三个隐含条件可知以上6个问题的解答为：

(3)sinB+sinC=sinB+

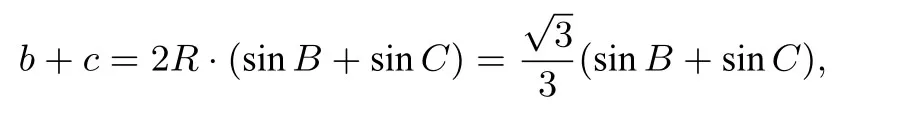
转化为问题(3)，最终得到b+c ∈(2,4].

(5)ΔABC的周长为a+b+c=2+b+c，转化为问题(4)，可得周长的最大值为6；

(6)ΔABC的面积为结合隐含条件3○，即余弦定理可得：4=b2+c2-bc≥2bc-bc=bc，当且仅当b=c时等号成立，故ΔABC的面积的最大值为

当然，这里也可用边转角的方法来解决，即：

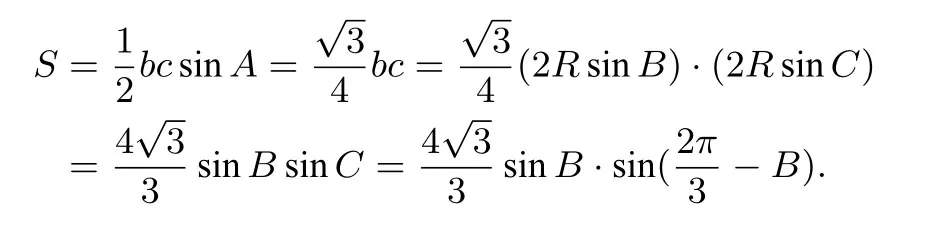
后略.

评析以上6个问题的求解过程，深刻的展现了解三角问题中已知一角及其对边的处理方法，揭示了三角形中边角之间的相互转化关系要靠正、余弦定理来实现.该系统总结不仅强化了对解三角形中边角关系的理解，而且求解过程中使用三角恒等变换化简三角函数式，利用三角函数图像求解范围的方法更是提升了学生对三角函数模块的掌握和使用，锻炼了学生的整体思维品质、数学素养和能力.

下面我们再以模型一的问题(4)为出发点，结合高考试题的考查方向和特点，继续深入探究解三角形中已知一边及其对角模型的一般方法.

例1如图，在ΔABC中，已知ΔABC的三个内角为A,B,C，其对应的三边为a,b,c，且A=60°，a=2，求b+c的取值范围.

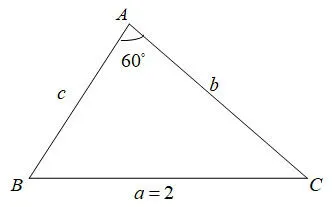
通法由题意知：故有b=2RsinB，c=2RsinC(实现了边的问题向角问题转化，使用正弦定理)，所以，

(转化为三角函数最值问题.)由于B+C=120°，故

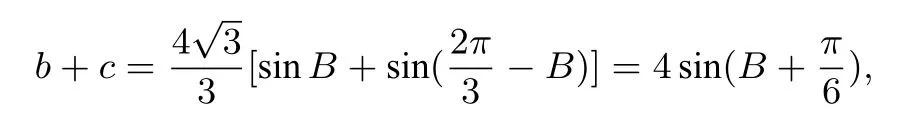
巧法由余弦定理知：4=b2+c2-bc=(b+c)2-3bc，由不等式知：

当且仅当b=c时等号成立，故得到b+c≤4，又由三角不等式知b+c＞a=2，综上可得：b+c ∈(2,4].

评析显然，巧法利用不等式放缩快速解决了问题，咋一看非常完美实用，但如果我们稍加改变问题中的条件或结果，那么巧法将黯然失色，看下面三个变式.

变式1在ΔABC中，已知ΔABC的三个内角为A,B,C，其对应的三边为a,b,c，且A=60°，a=2，求2b+c的取值范围.

变式2在锐角ΔABC中，已知ΔABC的三个内角为A,B,C，其对应的三边为a,b,c，且A=60°，a=2，求b+c的取值范围.

变式3在ΔABC中，已知ΔABC的三个内角为A,B,C，其对应的三边为a,b,c，且A=60°，a=2，求λb+µc(λµ0)的取值范围.

评析三个变式中，变式1条件不变，结论变为求解2b+c的范围，这是放缩法无法求解的.变式2条件加了“锐角”二字，就会使得b+c的取值范围中的下限发生变化，变为而不再是2，这样巧法求出的结果就会出错.但在通法的求解模式下，变式1、2均可顺利无误求解出正确结果，这无疑说明了掌握解决数学问题的通性通法的重要性，它可以直达数学问题的本质，以不变应万变.变式3是对整个模型问题的一般化总结，即“在已知三角形一角及其对边的条件下，求剩余两边的线性组合的取值范围”，这样将整个问题提高到了一般化的程度，提升了对解三角形问题的系统认知.不难发现，在模型一的体系下，问题(2)-(6)均可用边转角这一通法求解.

值得关注的是2012年全国课标卷文理科第17题、2010年全国课标卷理科第16题、2014年全国课标卷I理科第16题、2013年全国课标卷理科第18题、2016年全国课标卷I理科第18题、2017年全国课标卷I理科第18题都在考查解三角形中“已知一角及其对边”的模型，而且均在模型一的问题(1)-(6)中进行考查.如果我们一线教师在教学中结合以上经验，带领学生深入探究思考，在解三角形模型一的基础上提出问题：将模型一中的“已知一角及其对边”更改为“已知一角及其一条邻边”，会出现什么样的新问题呢? 2019年高考全国新课标卷Ⅲ文理科的第18题就给了我们答案!

模型二 已知三角形的一角及其一条邻边

例2(2019年高考全国卷Ⅲ文理科第18题)ΔABC的内角A,B,C的对边分别为a,b,c，已知bsinA.

(1)求B；

(2)若ΔABC为锐角三角形，且c=1，求ΔABC面积的取值范围.

解(1)根据题意由正弦定理得因为0＜A＜π，故sinA＞0，消去sinA得

由于0＜B＜π，0故或者而根据题意A+B+C=π，故不成立，所以又因为A+B+C=π，代入得3B=π，所以

(2)已知“三角形一角及一条邻边”的条件下求解面积的取值范围，这是区别于以往高考试题中的解三角形模型一的一个新的模型，结合三角形面积公式有：这里就产生了两种求解思路：一是将边转化为角；二是求出边a的取值范围.

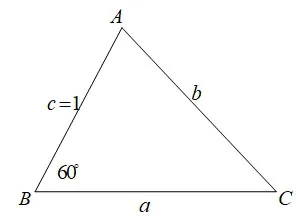
方向1受到模型一的启发，将边的表达式转化为角的表达式，即

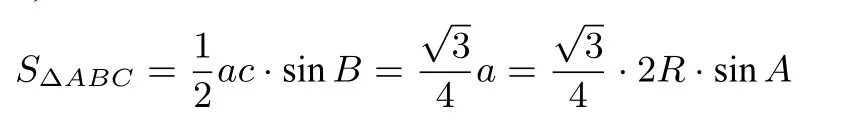
实现了结论由边向角转化，但已知一角及其邻边的条件下是无法计算出外接圆的半径R的，故此法不能解决问题.

采用技巧，根据c=1，则可构造出

的结构，这样利用正弦定理就有

法一如图，因为ΔABC是锐角三角形，由(1)知由A+B+C=π得到故解得由三角形面积公式有：

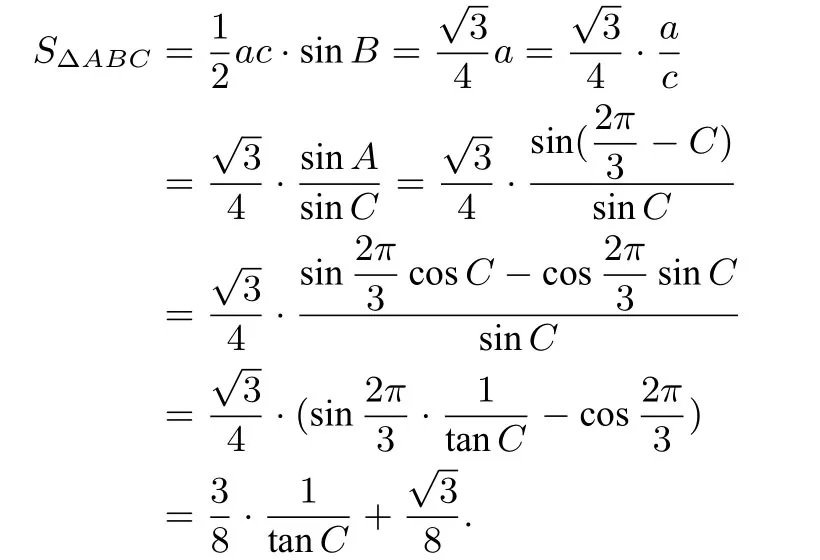
方向2由问题转化为是否能求出边的取值范围，考虑余弦定理求解.

法二因为ΔABC是锐角三角形，由(1)知由A+B+C=π得到故解得同理，由三角形面积公式有此时求出边长a的取值范围即可解决问题，据余弦定理有：

事实上，求出边a的取值范围是容易想到的，但实施起来由于“锐角”的控制以及计算的难度，导致此种解法困难较大.该题对于2019年高考的考生来说“题号”和“难度”并不匹配.

类比模型一提出的6个问题，我们可以对模型二中高考题的第(2)问进行深入探究拓展，也可以提出以下几个问题.

变式拓展

分析注意到ΔABC中，c=1，B=60°，结合余弦定理知：b2=a2-a+1，则：

三个变式结论都转化为了边a的表达式，故必须求出边

a的取值范围(即＜a＜2)，此时法二中使用余弦定理的思路就非常有效了.限于篇幅，读者可尝试解决以上拓展问题.

可以想象，2020年高考数学全国新课标卷中解三角形问题仍然将会是“宠儿”，望以上的论述能够给予备考的教师和学生一些帮助!