关于氢原子中电子出现概率最大位置问题的研究
2020-06-30张晓峰石凤良
张晓峰,石凤良
关于氢原子中电子出现概率最大位置问题的研究
张晓峰,石凤良
(唐山师范学院 物理系,河北 唐山 063000)
以基态氢原子和第一激发态氢原子为例,对氢原子中电子出现概率最大的位置及概率最大值问题进行了系统的分析讨论。
氢原子;概率;基态;第一激发态
自量子力学建立以来,氢原子问题[1-3]一直都是众多物理学家讨论的热点话题,而氢原子中电子出现的概率问题更是氢原子问题中的焦点。本文将通过对不同状态[4-5]的氢原子进行分析讨论,通过理论计算得出氢原子中电子出现概率最大的位置及概率的最大值。
1 氢原子中半径在的球壳内电子出现的概率分析



图1 电子在球壳内的分布

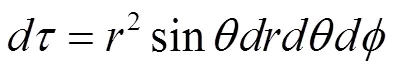


因为是归一化的,所以

化简得
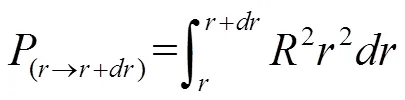
积分得


2 基态氢原子中电子出现最大概率位置的分析

0为玻尔半径[6],则有
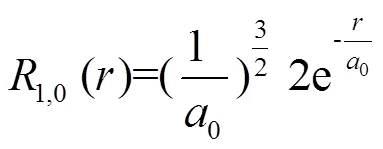
由归一化条件可知:

原式可化为

即


解得

带入得


3 第一激发态氢原子中电子出现最大概率位置的分析
3.1 主量子数n=2,角量子数l=1,磁量子数m=0时的最大概率位置
由(6)式知

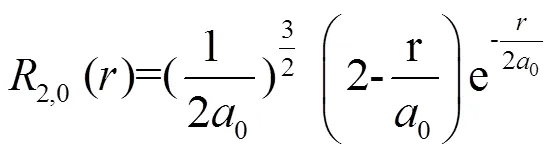
由归一化条件可知

(20)式可化为

即


得

整理得

令

(26)式可化为:

以下对3个解进行分析讨论。
满足条件,可近似为
代入(23)式得
满足条件,可近似为
代入(23)式得
两峰值作比较得
3.2 主量子数n=2,角量子数l=1,磁量子数m=0时最大概率位置
由(6)式知:


由归一化条件可知
原式可化为:

即


解得

带入原式,得
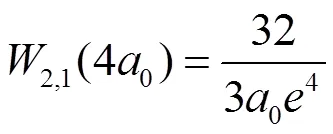

3.3 主量子数n=2,角量子数l=1,磁量子数m=1时或主量子数n=2,角量子数l=1,磁量子数m=-1时的最大概率位置
由(6)式知:



由归一化条件
原式可化为

即

3 结论与分析

两峰值作比较,得

[1] 喻力华,刘书龙,陈昌胜,等.氢原子电子云的三维空间可视化[J].物理通报,2011,30(3):9-10.
[2] 李金海,方恒忠,李子良.氢原子电子云密度分布分析[J].大学物理,2004,23(3):13-17.
[3] 曹铀.玻尔半径与径向分布[J].宝鸡师范学院学报(自然科学版),1992,14(2):48-50.
[4] 熊慧龄.氢原子不同状态下电子云径向分布和角度分布节面数的推引[J].化学通报,1979,47(3):77-83.
[5] 宋鹤山.量子力学[M].大连:大连理工大学出版社, 2006:150-151.
[6] 钱伯初.量子力学[M].北京:高等教育出版社,2006:17.
[7] 李加军.实系数一元三次方程的韦达定理及其应用[J].数学通讯,2017,85(9):43-45.
[8] 周世勋.量子力学教程[M].北京:高等教育出版社,2009: 67.
Study on the Position of Maximum Probability of Electron Occurrence in Hydrogen Atom
ZHANG Xiao-feng, SHI Feng-liang
(Department of Physics, Tangshan Normal University, Tangshan 063000, China)
Taking the ground state hydrogen atom and the first excited state hydrogen atom as examples, the position of the maximum probability of electron occurrence and the maximum probability of electron occurrence were systematically analyzed and discussed.
the hydrogen atom; the probability of; the ground state; first excited state
O413.1
A
1009-9115(2020)03-0063-04
10.3969/j.issn.1009-9115.2020.03.015
2019-07-02
2020-04-27
张晓峰(1997-),男,河北张家口人,本科生,研究方向为量子物理。
(责任编辑、校对:侯 宇)
