初中数学数形结合思想教学研究
2020-06-15王兴民
王兴民
【摘 要】初中是人生各种观念和思想形成的重要时期,作为教师要在这个时期培养学生正确的学习思想。数形结合的思想是整个初中数学学习过程的重要一步,数形结合能够把抽象难懂的数学知识正确运用数学图像后变得简单易懂,同时方便学生学习和理解。本文通过数形结合思想的重要性和现状,分析了数形结合在具体例题中的应用。作者根据自己的教学经验进行了数形结合思想在教学中的研究,供大家参考。
【关键词】初中数学;数形结合;数形转化;例题
一、初中数学数形结合思想的内涵和意义
数形结合是在找到题目中隐藏的数量之间的关系后用几何图形的形式表示出来,最后根据几何图形的概念和性质解决数学问题。在很长的研究过程中我们得出结论,数形结合的思想可以把复杂的数学问题变得简单化,能够直观、严密地解决问题,更加有利于学生的学习。
初中数学数形结合思想的意义表现在三个方面:①能够提升教师上课的效率;②数形结合思想能够让学生把抽象的问题简单化,即刻明白题目所要考察的内容,更加有利于学生的数学学习;③能够挖掘学生的思维。
二、现阶段初中学生在数学学习中的现状
(一)初中生对题目缺乏本质的认识,正确率低、做题慢
受应试教育的影响,从教师到家长,一直认为初中生学习的目的就是为了考上好的高中,继而考上好的大学,毕业后找个好点的工作。这样陈旧的思想就让初中学生对于学习没有一点自主性和创造性,在学习上习惯于死记硬背,不能举一反三。而且受传统教育的影响,教师很少花时间去培养学生的实践能力,这样就使学生遇到生活方面的题型时,似懂非懂,读不懂题就很难做对,正确率很低。所以数学教师在讲授课本上知识的同时也要加大学生对课外应用能力的培养,提高数学思想的培养。
(二)目前的初中学生遇到实际和抽象相结合的知识时不能考虑全面
到了初中,数学学习不像小学那样简单,数学知识开始变得抽象,不易理解,对学生来说难题也就相应增多。因此数学教师就要把培养学生的学习思想作为首要工作,把抽象的问题简单化,这就需要教师引入数形结合的思想。
三、数形结合在初中数学教学中的运用分析
(一)以数化形的运用
以数化形是在数学教学方式中将数字转化成图形,把抽象的知识转变为容易理解的几何图形,这样既可以帮助学生节省解题的时间,又锻炼了学生的数学思维。“数”转化成“形”中最关键的是如何找到数中所对应的形,这就要求数学教师找到抽象的数学问题相对应的数量模型,通过这个数学模型让学生直观地理解对应的问题。因为图形本身就具有直观性的特点,以数化形的作用就是为了避免逻辑推理的抽象问题,把抽象的数学变得直观,使数学问题变得简单化。
(二)以形变数的运用
以形变数是在几何教学中把图形中隐含的各个条件用代数的形式表达出来,使学生借助这些代数进行求解。虽然图形比数字有较强的直观性,能够把问题变得简单化,但是在初中的数学教学中对图形的定量计算时还需要利用代数把原本没有任何逻辑关系的图形转变成为“数”,通过数的分析、解答将图形中真正隐含的意义正确地表达出来。这同样需要数学教师在教学过程中要抓住图形和数之间的联系,从而使数所表达出来的数据切实符合图形要展现的意义,使图形所要表达的关系清晰化。以形变数的运用一般用在初中几何数学的问题处理中。
(三)数形互化的运用
数形互化是将以上两种形式的结合互变,是数形结合教学中最常使用的方法,通常用在直角坐标系和函数中,通过这种相互的转化可以用代数法对函数进行解答,也可以使几何中遇到的问题迎刃而解。初中数学存在的知识问题需要数形互化的思想来解决,这种方法的运用不仅能够提高解题的效率,还能让学生的数学思维能力得到很大的进步。
四、例题中数形结合的具体应用
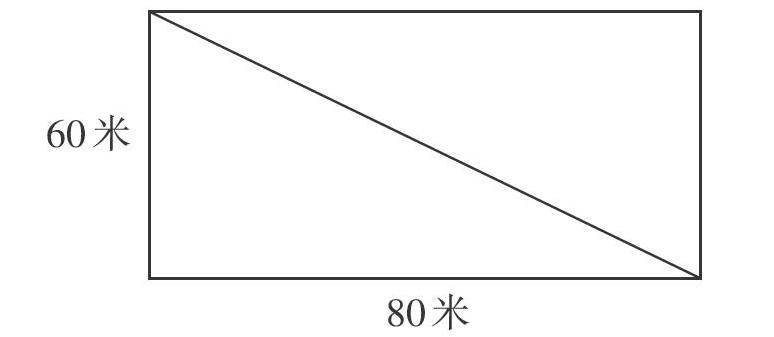
例题1:学校的操场草坪是长80米,宽60米的长方形,为了维护草坪,学校要在对角线位置修一条小路,问:小路的长是多少米?
很多学生在看到这个问题的时候都会感到迷茫,不知道怎样解题,找不到方向,有的学生也搞不明白题目本身的含义。这时候就需要数学教师利用数形结合的思想来解决。可以画出如下图形:
通过图形的直观展示,学生知道只要用到勾股定理就可以求出小路的长度是多少米。图形的出现让学生了解了题目要考察的内容,数形结合也使问题由抽象变得简单易懂。这样既提高了学生学习的效率,也解决了学生不理解题目的问题,更让学生增加了学习数学的自信,学习兴趣也会随之提高。
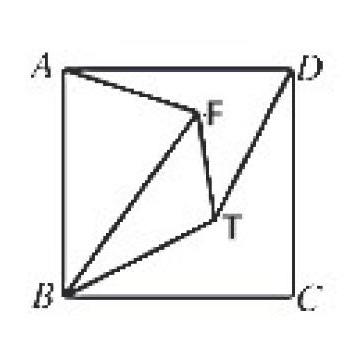
例题2:如图所示,在正方形ABCD中,点T、F是正方形内的两点,且TB=TD,FB=AB,∠FBT=∠CBT,求∠TFB。
此题如果只通过图形是很难解答的,这就需要通过题目中已知的信息,结合图形,通过图形转化成具体的数,再通过数量之间相等的数据推算出几个同等三角形的关系,最后得出答案。因此,初中数学教师可以根据教学内容的特点,形数结合,让学生了解“数”和“形”之间的内在联系,这样才能对课本的知识有更好的理解。
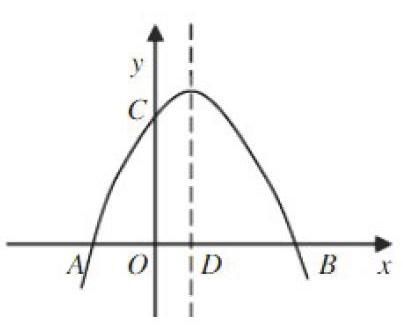
例题3:如图所示,在平面直角坐标系中,一抛物线与x轴分别相交于A、B两点,与Y轴相交于C点(0,5),顶点(1,4.5)。
(1)求抛物线的函数表达式;
(2)设抛物线的对称轴与X轴相交于D点,在对称轴上找出一点T,使△CDT为等腰三角形,并写出满足条件的所有点T的坐标;
(3)若点P是线段AB上的一个动点且不与A、B重合,分别连接AC、BC,过点P作PE//AC与线段BC相交于E,连接CE,若△CPE的面积是S,问S是否有最大值?若有最大值,求出这个最大值以及此时P点的坐标;若不存在,请说明理由。
此题涉及的范围广、知识点多,题中包含着抛物线、二次函数等知识难点,在初中数学中也属于难解题。看图比较容易得出(1)抛物线的函数表达式。在解(2)时,要考虑三点情况:①以C为顶点时的等腰三角形;②以D為顶点时的等腰三角形;③以T为顶点时的等腰三角形,根据三个顶点不同,运用数形结合分别解出答案。解(3)时,更需要利用数形结合的方法,结合二次函数、抛物线顶点的公式和三角形的面积求法进行解答。
由此可以看出数形结合法在初中数学教学过程中有着非常重要的作用。要想提升初中数学教学的发展,就要打开学生的解题思路,提高学生的解题速度,更要提升教师在数学教学的质量。
五、结语
初中数学作为初中教学中最重要的学科,要求学生能够学会运用基础知识,开拓思维,用心掌握这门学科中的技巧。数与形是初中数学中两个最基本的研究对象,代数的操作性强,便于学生把握;几何的直观性强,便于学生理解,两者的结合能够把初中数学中很多难解、抽象的问题变得直观、简化。
学生只有熟练地掌握了数形结合的思维方式之后,就能够发现这种相结合的思维方式的趣味性,也就提高了学生的学习兴趣。因此,数学教师要和学生一起携手,让数形结合思想真正存在于我们的脑海中,用来攻破更多的数学难题。
参考文献;
[1]林春安.初中数学数形结合思想教学研究与案例分析[J].读写算(教研版),2015(4).
[2]蒲志勇.数形结合思想在高中数学教学中的应用[J].数学学习与研究,2017(9).
(责任编辑 李 芳)
