基于改进匈牙利算法的导频分配

孙文胜，胡青红

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

0 引 言

随着生活中人工智能的大量引入，移动数据流量的需求迅速增长。大规模多输入多输出(Multiple-Input Multiple-Output，MIMO)技术逐渐从理论概念发展为未来无线网络的关键解决方案。大规模MIMO技术可按数量级提升蜂窝小区系统的频谱效率，无需为获取高数据传输速率在实际系统中部署更多的基站(Base Station, BS)[1]。在大规模MIMO系统中，每个BS都配备数百个有源天线阵列，提供前所未有的阵列增益和空间分辨率，每个小区的数十或数百个用户设备(User Equipment, UE)进行通信的同时，保持对用户间干扰的鲁棒性，大幅提升系统性能[2]。无线通信系统中，数据能否有效传输依赖上行链路和下行链路的信道状态信息(Channel State Information, CSI)，因此，在大规模MIMO系统中，获取准确的CSI信息是实现高质量通信的关键。在频分双工(Frequency Division Duplex, FDD)大规模MIMO环境中，信道互易性不再适用，这种情况下，如何获取更多信道信息成为主要问题[3]。时分双工(Time Division Duplex, TDD)模式下的大规模MIMO系统中，相比小区总人数，系统可用的正交导频资源数非常有限，如果为所有用户分配正交导频，随着用户数量的线性增加，系统将花费很大的导频开销[4]。为了减少导频开销，实际应用中，必然存在一些用户使用相同导频的情况，导致导频污染[5]。为了减少信道估计误差，提出了许多智能导频分配方案，例如可调相移导频(Adjustable Phase-Shift Pilot, APSP)算法可减少在宽带大规模MIMO系统中的获取信道状态开销。文献[6-7]采用以用户为中心的聚类方法来降低系统的计算复杂度，将系统环境作为一种分布式大规模MIMO，小区不存在边界，允许用户存在多个服务簇，每个用户从附近的BS中选择自己的服务簇，但是，基站获取的CSI信息受到导频复用的严重影响。文献[8-9]通过设计导频序列来减少大规模MIMO系统的导频开销，但当小区用户数量庞大时，此类方案计算复杂度急剧增大；文献[10]结合贪婪算法与功率控制问题对导频分配问题展开研究，但没有应用大规模MIMO系统的多天线阵列特性。此外，文献[11]提出的叠加训练序列设计的数据辅助信道估计和文献[12]提出的基于奇异值分解(Singular Value Decomposition, SVD)的盲信道估计算法，可用以获取准确CSI信息，但当应用于密集小区时，这两类方法的计算复杂性比较高。综合上述主流导频分配方案存在的弊端，本文结合小区用户分布特点和导频分配算法的计算复杂度，针对实际生活场景建模小区，制定了最大化MIMO系统的下行链路和速率的导频分配优化问题。

1 系统模型

图1 多小区用户的上行链路干扰模型系统

假设TDD模式下的蜂窝大规模MIMO系统存在L个小区，所有小区的范围大小相同并共享相同的时频资源。小区半径为R，BS位于小区中心，每个BS配有M根天线，每个小区中随机非均匀分布K个单天线用户，其系统模型如图1所示，图1中，实线表示BS的期望信号，虚线表示小区间的干扰信号。

在TDD模式下，上行链路中用户向基站发送导频序列，基站根据导频序列获取上行链路的信道状态信息CSI，并根据信道互易性获得下行链路的CSI，最后完成数据的发送。

(1)

式中，zlk为l小区内用户k的地理位置，zlk∈R2，满足随机分布；dj(zlk)为从BSj到小区l中的用户k的信道方差；根据系统信道互易特性，第j个小区的BS处接收的导频信号为：

(2)

式中，plk为在小区中分配给用户k的导频发射功率，n∈CM×τ为第j个BS处的加性噪声，元素独立分布为CN(0,δ2IM),δ2为噪声方差。

根据接收信号yj，第j个小区的用户k与第j个BS之间的最小二乘信道估计为：

(3)

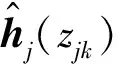
(4)

式中，pd为上行链路数据的传输功率，xlk为第l个小区中的第k个用户向第j个基站发送的数据信号，满足E[|xlk|]=1，Wj为信道噪声，满足CN(0,δ2IM)。

式(3)表示利用已知导频序列获取的信道估计值，由式(4)可知，在数据传输的下行链路中，接收端应用匹配滤波器(Matched Filter, MF)检测算法得到第j个小区k用户的接收信号表示为：

(5)

(6)

根据式(3)—(5)，可求得第j个小区中第k个终端的下行链路信号干扰和噪声比(Signal to Interference plus Noise Ratio, SINR)，表示为：

(7)

因此，下行链路第j个小区用户k可达和速率可以表示为：

(8)

式中，W表示总带宽，γ表示下行链路数据传输引起的频谱效率损失。

2 导频分配优化问题制定

考虑到系统导频污染和系统下行可达和速率紧密相关，本文制定了与导频分配相关的优化问题，如下所示：

(9)

式中，{μ}为所有小区可能的导频分配方法，θ(j,k)∈{φ1,φ2,…,φK}为第j个小区用户k的导频序列，式(9)最直接的方法就是采用穷举法，并且能通过穷举法获得最佳导频分配方案，但是，采用这种方法意味着必须尝试所有可能的分配方法，并且随着小区人数的增加，穷举搜索带来的计算复杂度呈指数增长，显然穷举搜索不可行。

为了降低计算复杂度，本文对上述问题进行简化，将L个小区的导频分配分解成L个子问题，子问题复杂度远远小于O(K!)，总复杂度小于O(L×K!)；应用对应算法经过多次迭代解决每个子问题，同时需要预先固定其它L-1个小区的导频分配，通过优化当前小区的导频分配，最后达到最佳分配。因此，得到如下子问题：

(10)

式中，θj为当前对第j个小区正进行分配的导频序列，θ-j为除小区j外的其它小区已提前随机分配导频序列，R′为当前所有小区的下行可达和速率。因此，对于式(10)，开始时除特定小区外，其它小区的采用导频资源随机分配，预先确定其它小区的导频分配矩阵，随后针对特定小区的导频进行最优分配。

式(10)表示的导频分配策略在分解前后并没有利用小区用户位置的特点；获取最佳导频分配需要在一定的条件下最小化导频复用的影响，由式(4)和式(5)可知，相比于目标小区用户的信号强度，其它小区用户的干扰强度不可忽略时，目标小区接收其它小区的导频信号，由于不同小区使用同一组正交导频，此时不同小区间产生导频复用。

3 导频分配算法

本文对小区用户进行分类，分为第Ⅰ类用户和第Ⅱ类用户。目前许多文献关于用户分类都是基于用户空间位置信息对用户进行分类，优化导频分配方案即最大程度减小信道估计误差，对此，本文定义一个信道误差度量因子(Channel Error Metric，CEM)[13]：

(11)

其期望值可表示为：

Δjk=E{Δjk}

(12)

式(11)表示任何相干时间信道估计误差与真实信道之间的瞬时变化值，式(12)代表某特定时间内的相对变化稳定值，针对具有多根天线的用户小区，基于最小均方误差(Minimum Mean Square Error, MMSE)估计算法的信道误差度量因子的闭式表达式如下：

(13)

式中，plk为导频发送功率，βjlk为系统的大尺度衰落系数；并且，当基站天线数M→∞，进一步精确表达式(13)为：

(14)

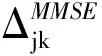
在实际应用中，虽然小区用户数量庞大，但是受到严重导频污染影响的用户相对较少，K′≪K，因此本文对第Ⅰ类用户采用穷举搜索法，找出Ⅰ类用户的最佳导频分配。多小区用户分类算法与第Ⅰ类用户导频分配算法实现如下。

初始化：输入阈值γ，小区数L，用户数量K，用户导频功率pjk

步骤1：forj= 1∶L

①初始化信道各项参数γ，L，K，pjk

②根据公式(2)计算目标基站j接收到的导频信号yj

③为获取高精度的信道估计值，将对式(3)采用最小均方误差准则进行信道估计，得到各用户的信道估计矩阵

(15)

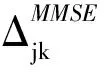
⑤用户分类：

fori=1∶K

End

用户的start[j]经过降序排列，最后得到descend[j]

⑥根据提前设定的合适阈值γ，对排序后的CEM对应的用户进行分类，低于γ的用户归为第Ⅰ类用户，并存于 ClassⅠ[j]，否则为第Ⅱ类用户，对应用户存于ClassⅡ[j]

End

步骤2：求出每个小区的ClassⅠ[j]中元素数量的最大值，得到K′。

(16)

其中

(17)

本文将一对一匹配问题转换成上述问题的解决形式，针对每个子问题通过应用改进匈牙利算法获得最佳导频分配。随后，移动到下一小区并使用相同的方法来优化下一个子问题的导频分配。第Ⅱ类用户采用的改进匈牙利导频分配算法实现如下。

初始化：输入小区数量L，导频数=用户数K，迭代容忍阈值ε，迭代索引t=1，小区索引j=1

步骤1：根据小区数量和小区用户数构建当前小区模型

步骤2：获取各小区Ⅰ类用户的导频分配结果，提前固定Ⅰ类用户的导频序列

步骤3：接下来对各小区剩余的正交导频数进行分配，采用匈牙利算法获取当前第j个小区的最佳导频分配结果θj，获取此时所有小区的导频分配结果μt

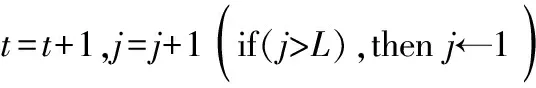
步骤5：如果R{μt+1}-R{μt}<ε,则重复步骤3—5

步骤6：结束分配，获取导频分配结果μt

在解决每个子问题(迭代)时，根据匈牙利算法获得导频分配，并且在该优化(迭代)中使系统的总和率最大化。因此，式(16)的目标在每次迭代中增加直到收敛。

从计算复杂度方面对算法性能进行分析，从两个方面对算法复杂度进行分析。

(1)用户分类。根据信道特点，对信道误差进行分析，需要遍历各个小区的用户数，因此，需要付出的计算量为O(LK)。

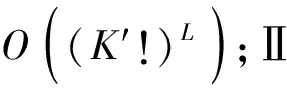
4 仿真实验与分析

假设小区单元半径R=750 m，每个BS配备有M个天线，基站位于小区中心，仿真参数如表1所示，根据蜂窝小区位置、用户位置随机特点以及小区用户参数构建的小区模型如图2所示。

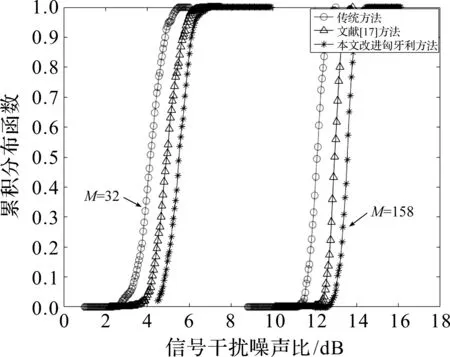
分别采用传统随机导频分配、文献[14]的导频分配方法和本文提出的改进匈牙利方法得到的系统下行链路平均SINR累积概率分布(Cumulative Distribution Function, CDF)曲线如图3所示。可以看出：随着天线数量的增加，下行链路的SINR得到改善，基站天线的数量由32增加到158时，下行链路的SINR提高了近7 dB。天线数目为158时，对比传统随机分配方案，文献[14]方法的下行链路的SINR提升近2 dB，相比于文献[14]方法，本文提出的改进匈牙利算法提升了近1.5 dB，说明本文提出的方案改善了导频复用带来的影响。

表1 多小区用户模型仿真参数

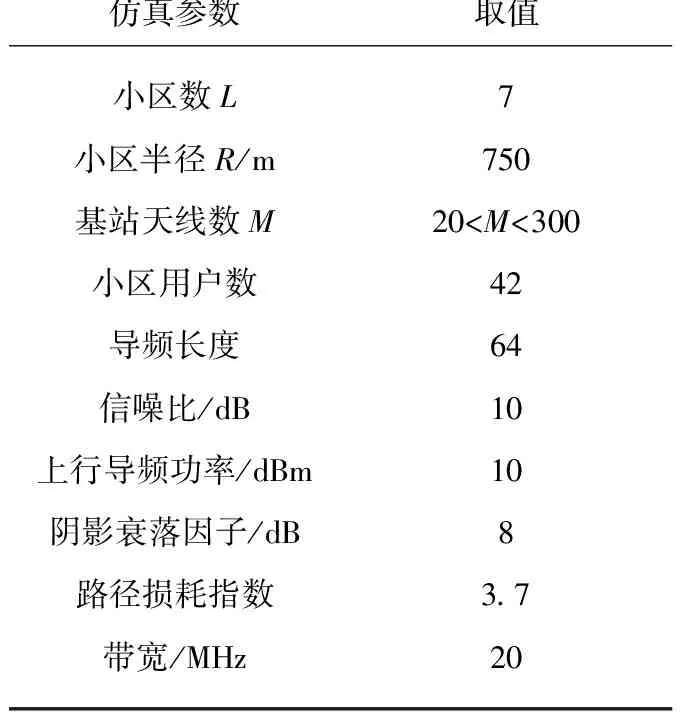
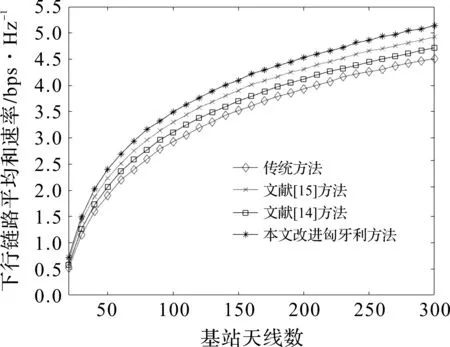
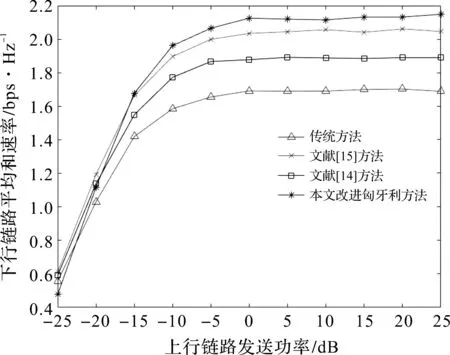
仿真参数取值小区数L小区半径R/m基站天线数M小区用户数导频长度信噪比/dB上行导频功率/dBm阴影衰落因子/dB路径损耗指数带宽/MHz775020

图2 多小区用户模型

分别采用传统随机导频分配、文献[14]的导频分配方法、文献[15]的导频分配方法和本文提出的改进匈牙利方法对系统小区的下行链路平均和速率与基站天线数M的关系进行仿真，结果如图4所示。可以看出：当M>50时，考虑系统导频资源有限，相比于传统方案，文献[14]和文献[15]方法的平均可达和速率提升了约0.25 dB和0.35 dB，相比于文献[15]方法，本文提出的改进匈牙利算法提升了近0.2 dB。

图3 下行链路平均SINR累计概率分布

图4 下行链路平均和速率与基站天线数的关系

采用传统随机导频分配、文献[14]的导频分配方法、文献[15]的导频分配方法和本文提出的改进匈牙利方法得到的下行链路和速率随上行链路功率变化曲线如图5所示。可以看出：当下行发送功率小于-15 dB时，4种导频分配方案的下行链路平均和速率无明显差异；发送功率大于-10 dB后，随着发送功率的增加，4种导频分配方案的下行链路平均和速率均增大，本文算法的提升最明显；发送功率大于10 dB时，4种导频方案的下行链路平均和速率变化均趋于平稳。

考虑导频资源有限情形，图6对上行链路发送功率与下行链路平均和速率关系进行仿真。可以看出：当上行链路发送功率小于-20 dB时，4种导频分配方案平均和速率曲线接近重合，且系统下行链路平均和速率随着发送功率的增大而增大；当发送功率大于-15 dB且小于5 dB时，系统下行链路平均和速率随着发送功率的增大而增大，与传统方案相比，文献[14]和文献[15]方法分别提高了0.2 dB和0.35 dB，相比文献[14]和文献[15]方法，本文提出的改进匈牙利算法分别提升了近0.3 dB和0.1 dB；当发送功率大于5 dB时，4种导频方法的平均和速率均趋于平稳。

图5 下行链路平均和速率与下行链路发送功率的关系

图6 下行链路平均和速率与上行链路发送功率的关系

5 结束语

为了减少导频污染带来的影响，本文将存在严重导频污染的用户进行分类，针对两类用户在数量上的特点，采用一种低复杂度的改进匈牙利导频分配方案，对Ⅰ类用户采用穷举搜索法，为Ⅱ类用户制定导频分配优化问题。改进算法提高了系统下行链路可达和速率，性能表现良好，能以较低的计算量准确获取信道状态特性。下一步将从导频序列设计出发，进一步减轻系统导频污染。