一类时变时滞系统改进的稳定性准则

唐 亮，姜偕富，尹宗明，刘丽丽

(杭州电子科技大学自动化学院，浙江 杭州 310018)

0 引 言

时滞现象存在于大多数的实际系统中，往往导致系统性能变差甚至使得系统失去稳定。因此，对时滞系统稳定性的研究不仅具有理论意义，而且具有重要的实际应用价值。过去的几十年间，时滞系统的稳定性分析已成为各个领域的研究热点之一，并取得很多优秀的研究成果[1-7]。文献[1]将系统时滞分解为两个部分来分析T-S模糊时滞系统的稳定性，取得一个保守性较小的稳定性准则。文献[2]采用Wirtinger积分不等式来处理L-K泛函求导过程中产生的积分项，在一定程度上减小了系统稳定性准则的保守性。文献[3]采用凸组合不等式来研究T-S模糊系统的稳定性，获得了很好的结果。文献[4]在构造L-K泛函时引入三重积分来研究具有时滞的不确定性系统的鲁棒稳定性问题，得到一个具有较小保守性的稳定性准则，但该三重积分的内层积分上限中未能充分考虑时滞信息。同样，文献[5-7]所采取的方法都获得了较好的结果，但在L-K泛函的构造上也未能充分考虑时滞上下界的信息，仍可进一步减小所得结果的保守性。本文针对一类时变时滞系统的稳定性问题，充分利用时滞信息，构造一个改进的L-K泛函，将更多的时滞信息加入到了该泛函的三重积分内层积分上限中，并给出一个与现有文献相比具有较小保守性和决策变量较少的时滞系统的稳定性准则。

1 系统模型

考虑如下线性时变时滞系统

(1)

(2)

式中，h1，h2和d为常数且d>0。

2 主要结果

(3)

(4)

(5)

(6)

Δ44=-Q3-4R2-4αR2，

Δ12=-P12+P13+P14-2R1，

Δ15=ATP12+P22+6R1/h1+h1S1，

Δ23=-2R2-α(Y11+Y12+Y13+Y14)-(1-α)(Y21+Y22+Y23+Y24+2R2)，

Δ24=(1-α)(Y21-Y22+Y23-Y24)+α(Y11-Y12+Y13-Y14)，

Δ34=-2R2+(1-α)(-Y21+Y22+Y23-Y24)+α(-Y11+Y12+Y13-Y14-2R2)，

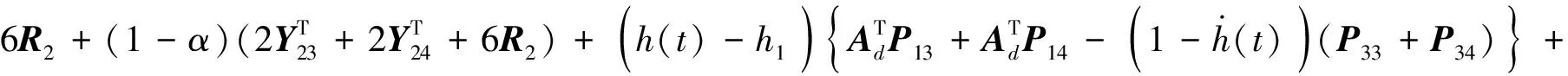
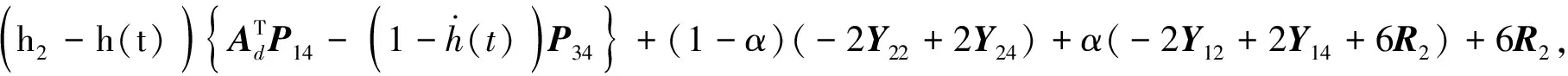
Δ67=-4(1-α)Y24-4αY14，

证明构造如下L-K泛函对系统(1)进行稳定性分析

V(t)=V1(t)+V2(t)+V3(t)+V4(t)

(7)

式中，V1(t)=ωT(t)Pω(t)，

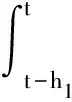
V(t)沿系统(1)轨迹对时间t求导得到：

(8)

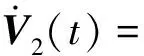
(9)

(10)

(11)

对式(10)中积分项使用文献[8]中的引理1得：

(12)

(13)

(14)

由式(2)可知，h2+h(t)-2h1≤2h12成立，对式(11)中积分项使用文献[10]中的引理2得：

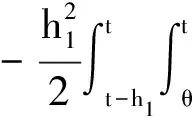
(15)

(16)

结合式(8)—(16)得：

(17)

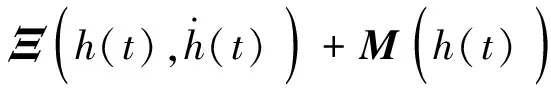
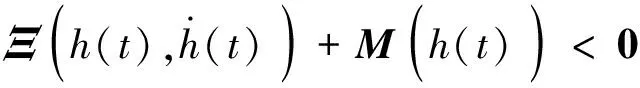
(18)

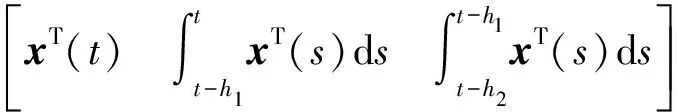
3 数值示例

使用如下系统模型

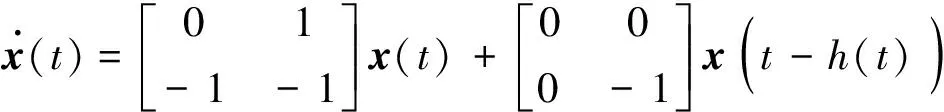
当h1=0.4，d取不同值时，通过使用MATLAB中的LMI工具箱求得基于本文定理所允许的最大时滞上界h2，并与相关文献进行对比，结果如表1所示。表1中，n为系统维数。

表1 d取不同值时，取得的最大时滞上界h2

从表1可以看出：使用本文定理取得的最大时滞上界比使用文献[5]、文献[6]和文献[7]相关定理取得的最大时滞上界大，说明本文所得到的稳定性准则具有较小的保守性。此外，通过表1中最后1列可以看出：本文算法的决策变量数比文献[5]、文献[6]和文献[7]少，因此，本文得出的稳定性准则具有较高运算效率。综上，本文得到的稳定性准则具有较小的保守性和较高的运算效率。

4 结束语

本文主要研究时变时滞系统的稳定性分析问题，充分考虑时滞信息，在构造L-K泛函时，将更多时滞信息加入到引入的三重积分项中，采用Wirtinger积分不等式的方法来处理L-K泛函求导过程中出现的积分交叉项，得到具有较小保守性和较高运算效率的稳定性准则。但是，实际应用中，控制系统还会受到外部干扰或者自身变化等不确定因素的影响，下一步将对该时滞系统进行鲁棒H∞稳定性分析和控制器设计。