基于Tent映射的图像加密算法及其实验研究
2020-06-08李付鹏刘敬彪王康泰
李付鹏,刘敬彪,王康泰
(杭州电子科技大学电子信息学院,浙江 杭州 310018)
0 引 言
随着数字媒体技术的发展,图像保密的需求日益增加,然而数字图像信息量大,冗余度高,使用传统的随机序列进行加密使得数据传输量较大。混沌系统能够产生伪随机序列作为密码序列,不仅能有效减少信息传输量,而且能获得更大的密钥空间。近年来,混沌系统应用于图像加密成为热点,通过混沌系统获取伪随机序列对图像进行加密成为有效的加密方法。C.E.Shannon[1]提出十分有效的加密算法——置乱和混乱。置乱和混乱有效打破了图像像素之间的关联,利用混沌序列的随机性对明文图像数据进行加密,从而掩盖图像信息,达到保密效果。通过统计分析和随机性测试可以对加密的安全性进行表征[2]。文献[3]对一种超混沌图像加密算法的安全性进行了分析并改进加密步骤,获得良好的统计分析和测试结果。但是,文献[4]证明其不能抵御已知明文攻击,算法的抗攻击能力弱于声明的抗攻击能力。使用混沌序列的伪随机特性对明文图像进行加密能有效掩盖明文信息,但密文扩散过程需要进一步与明文相关联。使用混沌伪随机序列与明文数据求异或运算的加密算法虽能将明文有效掩盖,获得难以分辨的图像外观,但异或运算对全零明文敏感,对仅使用异或运算的加密算法选择明文攻击易获取其等效密钥。因此,应在原有混沌加密的基础上有针对性地增强对已知明文攻击的防御。另外,为了降低混沌序列的随机性,加密过程中求异或运算需要将密文序列限定为不大于像素最大值的整数,导致置乱和混乱加密过程中混沌系统产生的密钥运算精度有限,混沌系统的连续状态被离散化,混沌轨道被限制在2N(N为图像编码位数)的离散空间内。文献[5]指出:无论是一维混沌系统还是高维超混沌产生的混沌序列都存在数字化后有限精度问题。文献[6]提出通过增强密钥与明文的关联来提高保密性能。针对选择明文攻击的选择性及数值计算有限精度问题,本文提出一种基于Tent映射的应对方案,加密算法使不同的明文对应不同的混沌参数,增强了密钥与明文之间的联系。
1 Tent映射
Tent映射定义为
(1)
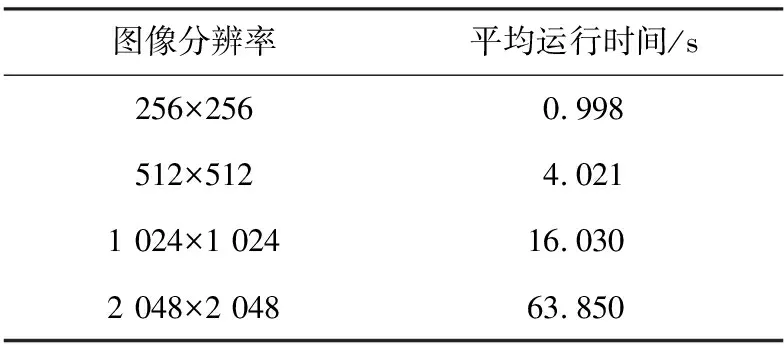
式中,Xn∈(0,1),n∈N+。图1(a)是Tent映射分岔图,图1(b)是控制参数0 图1 Tent映射分岔图及其李雅普诺夫指数 已知明文图像PM×N的i行j列处图像像素为pij。提取明文图像PM×N的k个特征点值用来计算系统加密密钥。 [s1,s2,…,sk]=f(PM×N) (2) 使用MATLAB软件对选取的像素为512×512,8位深度的数字明文灰度图像Lina.jpg按照加密算法设定的加密步骤进行加密、解密测试。 图2 明文图像直方图 本文密钥选取图像像素均值,对应像素均值向下取整所得像素值的像素点数以及直方图的局部峰值点和局部谷值点,如图2标记点所示。sk为选取的像素值,sk+1为对应的像素数,k∈1,3,5,…。 (3) 式中,max(·)表示取数列的最大值。 密文隐藏过程公开图像需要获得两倍于明文图像的列数,所以为了得到与明文图像相同分辨率的密文图像,需要将明文图像进行压缩采样,采样后明文图像列数减少一半。奇数行取pi,2j-1,偶数行取pi,2j。与文献[8]解密时对获取的解密图像进行双线性插值得到与明文图像相同行列数的图像。 MATLAB仿真的加解密效果如图3所示,对比图3(a)与图3(b),密文图像像素杂乱无章,图像信息被掩盖。对比图3(a)与3(d)可以看出图像解密后图像信息恢复较完整,损失较少。图3(e)是使用错误的密钥对密文解密结果,图像像素为随机分布,且不能辨别任何细节。对比图3(c)与3(f)可以看出隐藏密文对载体图像影响微小。 图3 对Lina图加解密对比及隐藏后载体图像对比 实验验证本文算法时,算法的置乱和混乱步骤的数值计算精度全部为10-16,可得密钥空间理论值大于10106,可以有效抵御密文攻击[8]。加密过程的置乱操作初值X1=0.877 567 458 719 291,控制参数a=1.531 372 549 019 608,将参数X1,a的最低位小数增加或减小1,解密后得到类似图3(e)所示的错误解密图像。 图像像素改变率(Number of Changing Pixel Rate,NPCR)和归一化平均变化强度(Unified Averaged Changed Intensity,UACI)是评价抗差分攻击能力的重要指标,考察明文图像某像素点灰度值的轻微变化引起整个密文图像发生改变的情况[9]。明文图像为PM×N,则M,N为图像的行数与列数,C1为PM×N加密所得密文图像,对改变PM×N中某一点的像素值(像素值加1或减1)所得图像加密后得到新的加密图像C2。图像的NPCR的计算公式为 (4) UACI的计算公式为 (5) 对不同分辨率的Lina图像进行NPCR和UACI测试,结果如表1所示。 表1 NPCR和UACI测试结果 表1中的测试结果表明:明文图像稍微变化会引起密文图像的剧烈变化,但与NPCR和UACI测试结果的理想值有差距,虽然不能认为明文图像稍微变化加密后密文是随机相关的[10],但测试结果也表明加密算法有较强的抵御差分攻击的能力。 对图像所有像素值3个方向的相邻像素相关系数进行计算求得图像像素相关系数σxy,在图像中选取水平方向相邻像素对(Pi,j,Pi,j+1),竖直方向相邻像素对(Pi,j,Pi+1,j),对角线方向相邻像素对(Pi,j,Pi+1,j+1)。式(5)中xi,yi分别表示像素对的前后2个值。 (6) 表2 图像相关系数分析 计算加密前后图像三方向的σxy系数并与其它文献加密算法对比,所得结果如表2所示。 加密后密文图像的相邻像素σxy系数与原图相邻像素相关性差别很大,由高度相关性(σxy→1)变为几乎不相关(σxy→0)[14]。与表2中文献[11]、文献[12]和文献[13]的相应结果对比,部分方向上取得了更低的相关性(σxy→1)系数。 熵是用来描述事物的复杂性,信源的信息熵是度量信息随机性的一个重要参考指标。计算公式如下: (7) 式中,p(Si)为信号Si的概率,n为表示每个信号的二进制位数。因此,从理论上来讲,对于8位二进制表示的灰度图像,理想情况下密文图像的信息熵应该等于8,H(S)值越接近8则说明密文随机性越好。本文加密后密文的信息熵为7.938,接近理想值。 表3 不同分辨率灰度图像加密耗时对比 加密运算速度影响加密效率,因此加密算法应该具有快速的执行速率,良好的并行运算能力。实验对不同分辨率的灰度图像进行加密耗时测试,测试使用在core(TM)1.8 GHz处理器,16 GB内存上运行的Windows10系统上安装的MATLAB2018A。测试结果如表3所示。 由表3可以看出:运行时间与图像像素数成线性关系,加密算法的消耗时间是可预期的。 本文提出一种基于Tent映射的图像加密算法,改进了加密过程的混乱步骤。算法未将密钥通过运算变换到区间[0,255]内,保留了密钥的高精度数据,从而增大密钥空间。加密过程中密钥仅对数据进行排序,不与数据进行异或运算,有效避免了使用特殊图像来获取等效密钥。但是,加密时对明文图像进行了裁剪,图像信息有部分损失。如果将明文图像加密隐藏到2幅载体图像中则可以无损地复原图像,下一步将继续改进。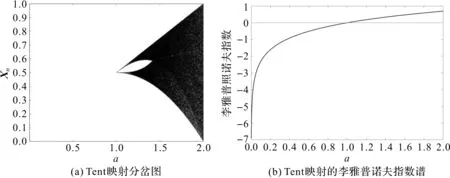
2 混沌加密隐藏算法
2.1 密钥设置
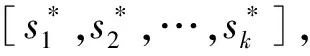
2.2 置乱算法

2.3 混乱算法
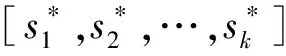
2.4 解密算法
2.5 密文图像隐藏

3 图像加密实验验证

3.1 图像特征点值选取

3.2 图像压缩与加密
3.3 图像解密

4 加密性能分析
4.1 密钥空间
4.2 NPCR和UACI分析


4.3 混沌加密相邻像素相关性分析

4.4 信息熵分析
4.5 加密速度分析
5 结束语
