结构可靠性优化的多输出高斯过程代理模型
2020-05-23赵维涛刘照琳祁武超
赵维涛,刘照琳,祁武超
(沈阳航空航天大学 航空宇航学院,沈阳 110136)
1 引 言
为合理考虑不确定性对结构优化的影响,学者们提出了基于可靠性设计优化RBDO(Reliability-Based Design Optimization)的概念[1,2]。在过去的几十年中,对RBDO问题提出了双循环法、单循环法和解耦法。虽然这些算法在理论上可以较好地解决RBDO问题,但对于复杂结构,特别是具有多失效模式的结构,可靠度计算较耗时。为解决这一问题,学者们提出了代理模型。目前,高斯回归过程模型[3-5]已成为最具代表性的代理模型之一。高斯回归过程模型可分为单输出高斯过程SOGP(Single Output Gaussian Process)[6]与多输出高斯过程MOGP(Multiple Output Gaussian Process)模型[7,8]。SOGP仅对单个极限状态函数进行建模,在模型构建过程中未考虑各极限状态函数之间可能存在的相关性;而MOGP引入了协方差矩阵,可模拟各失效模式之间可能存在的相关性。在实际工程中,具有共同输入的多个极限状态函数之间必然存在相关性。因此,在代理模型构建过程中考虑极限状态函数间的相关性是必要的。
通常MOGP模型与学习函数相结合,以平衡其精度和效率。常用的学习函数有期望可行性函数EFF(Expected Feasibility Function)[9]、U函数[10]、H函数[11]和最少改进功能[12]等。学习函数用于从训练样本中筛选对提高MOGP模型预测精度有利的样本点。MOGP模型主要用于结构可靠度计算,初始样本和训练样本均以随机变量均值点为中心,依据随机变量的分布形式生成,样本点主要集中在随机变量均值点附近,导致MOGP模型全局近似精度不佳,在优化过程中可能需要重新建模[9-12]。
本文首先利用Bucher方法生成初始样本并构建初始MOGP模型,其次在设计空间内均匀布置训练样本以保证训练样本的均匀性,确保训练后的MOGP模型具有较好的全局近似精度,最后利用训练后的MOGP模型采用RIA(Reliability Index Approach)[1]、PMA(Performance Measure Approach)[2]与SORA(Sequential Optimization and Reliability Assessment)[13]求解RBDO问题。
2 代理模型
2.1 MOGP模型
MOGP模型的数学表达式为
y(·)~N(h(·)B,Σm × mR(·,·))
(1)
式中h(·)为基函数矢量,B为回归模型的回归系数矩阵,Σm × m为协方差矩阵,R(·,·)为相关函数,m为输出矢量个数(即失效模式个数)。
相关函数采用高斯指数模型,并采用最大似然估计相关参数。在估计出未知参数B和Σm × m与相关参数之后,任意输入矢量x的预测值μy(x)与方差Σy(x)的表达式为
μy(x)=(h(x)B)T+(Σm × m⊗r(x))×
(Σm × m⊗R)-1vec(Y-HB)
(2)
Σy(x)=Σm × m-(Σm × m⊗r(x))×
(Σm × m⊗R)-1(Σm × m⊗r(x))T
(3)
式中H为样本点所对应的基函数矢量构成的矩阵,r(x)为输入矢量与样本点构成的相关函数矢量,R为相关函数矩阵,Y为样本点输出矩阵,⊗是克罗内克积运算符。
MOGP与SOGP的主要区别在于,MOGP引入了协方差矩阵来表示各极限状态函数之间可能存在的相关性。若各失效模式之间存在相关性,则协方差矩阵中各元素非零;若各失效模式之间不存在相关性,则协方差矩阵为对角矩阵。协方差矩阵可由构建MOGP模型的样本点确定,其表达式为
(4)
式中Nt为构建MOGP模型的样本点数量。
2.2 学习函数
基于MCS计算结构失效概率的公式可知,在利用代理模型并结合MCS计算结构失效概率时,对结构失效概率起决定性影响的是极限状态函数的符号。因而,如果MOGP模型能够对极限状态极限函数的符号精准预测,则可得到较为准确的失效概率。基于这种思想学者们开发了主动学习函数来提高MOGP模型的预测精度,目前已提出多个学习函数,其中Echard等[10]开发的U函数简单可靠,其表达式为
(5)

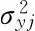
(6)
式中r与mj为串并联系统中串联与并联个数。
3 RBDO问题
3.1 可靠性指标法
在双循环方法中,概率性约束描述为可靠性指标不小于目标可靠性指标,此种描述方法称为可靠性指标法RIA[1]。其数学表达式为
min.C(d)
(7)
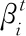
3.2 功能度量法
功能度量法PMA[2]是一种逆可靠度分析的方法,采用概率功能度量值衡量可靠性,具体表述为在目标可靠性指标条件下的概率功能度量值不小于0。其数学表达式如下,
min.C(d)
(8)
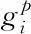
3.3 序列优化与可靠性评估
序列优化与可靠性评估方法SORA[13]是将设计变量优化与可靠度计算依次循环的方法。在每次循环中包含两个部分,一部分为基于设计变量的确定性优化,另一部分为基于PMA的可靠性分析。其数学表达式为
min.C(dk)
(9)
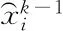
4 本文方法
本文方法的具体流程如下。
(1) 采用Bucher方法生成初始样本并计算与之对应的结构响应; (2) 基于初始样本构建初始MOGP模型; (3) 在整个设计空间内均匀布置训练样本105~106个; (4) 利用已构建的MOGP模型计算训练样本的预测值μy(x)与方差Σy(x);(5) 利用预测值μy(x)与方差Σy(x)计算训练样本点对应的U函数值; (6) 寻找训练样本中具有最小U函数值的样本点x*。当U(x*)≥2时,跳转至步骤(10),否则计算x*对应的结构响应; (7) 将x*与其响应值分别加入初始样本输入和输出矩阵,并将该样本点从训练样本中删除; (8) 基于更新后的初始样本修正MOGP模型; (9) 跳转至步骤(4); (10) 利用已构建的代理模型,分别采用RIA和PMA与SORA求解RBDO问题。
从以上流程可以看出,本文方法分为代理模型构建和基于可靠性的结构优化两部分,且这两部分完全分离,即先构建代理模型,然后利用已经建立的代理模型开展基于可靠性的结构优化,代理模型的构建不受结构可靠度以及优化算法的限制。
5 数值算例
算例1具有三个串联概率约束的RBDO问题[14,15]定义为
min.f(d)=μx1+μx2
(0.0≤μxi≤10.0,σxi=0.3 (i=1,2))
(10)
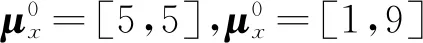
当初始样本中心取为不同值时(对应图1~ 图3 ),MOGP模型构建所需调用真实模型次数分别为9+36,9+36和9+33,相差无几,进一步说明本文方法对初始样本中心不敏感。
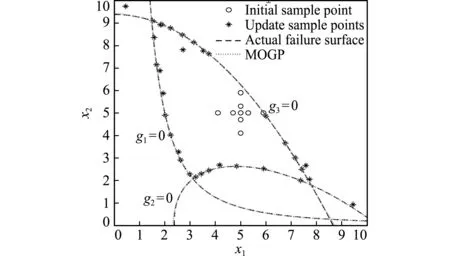
图1 算例1的MOGP模型(初始样本点-1)
Fig.1 MOGP of example 1(initial sample point-1)

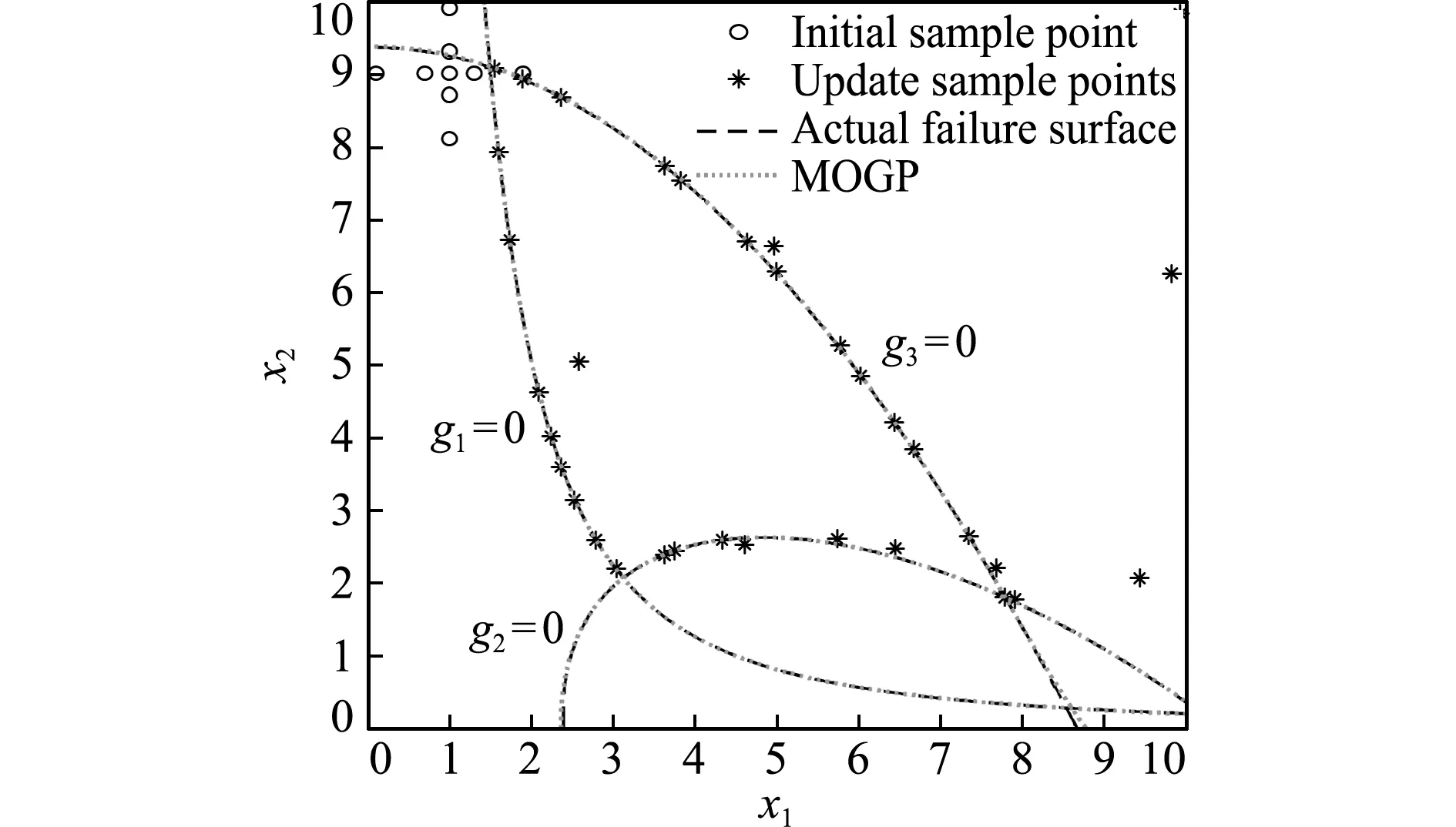
图2 算例1的MOGP模型(初始样本点-2)
Fig.2 MOGP of example 1(initial sample point-2)
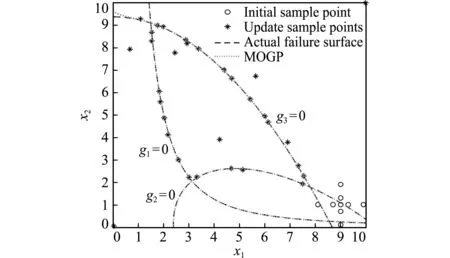
图3 算例1的MOGP模型(初始样本点-3)
Fig.3 MOGP of example 1(initial sample point-3)
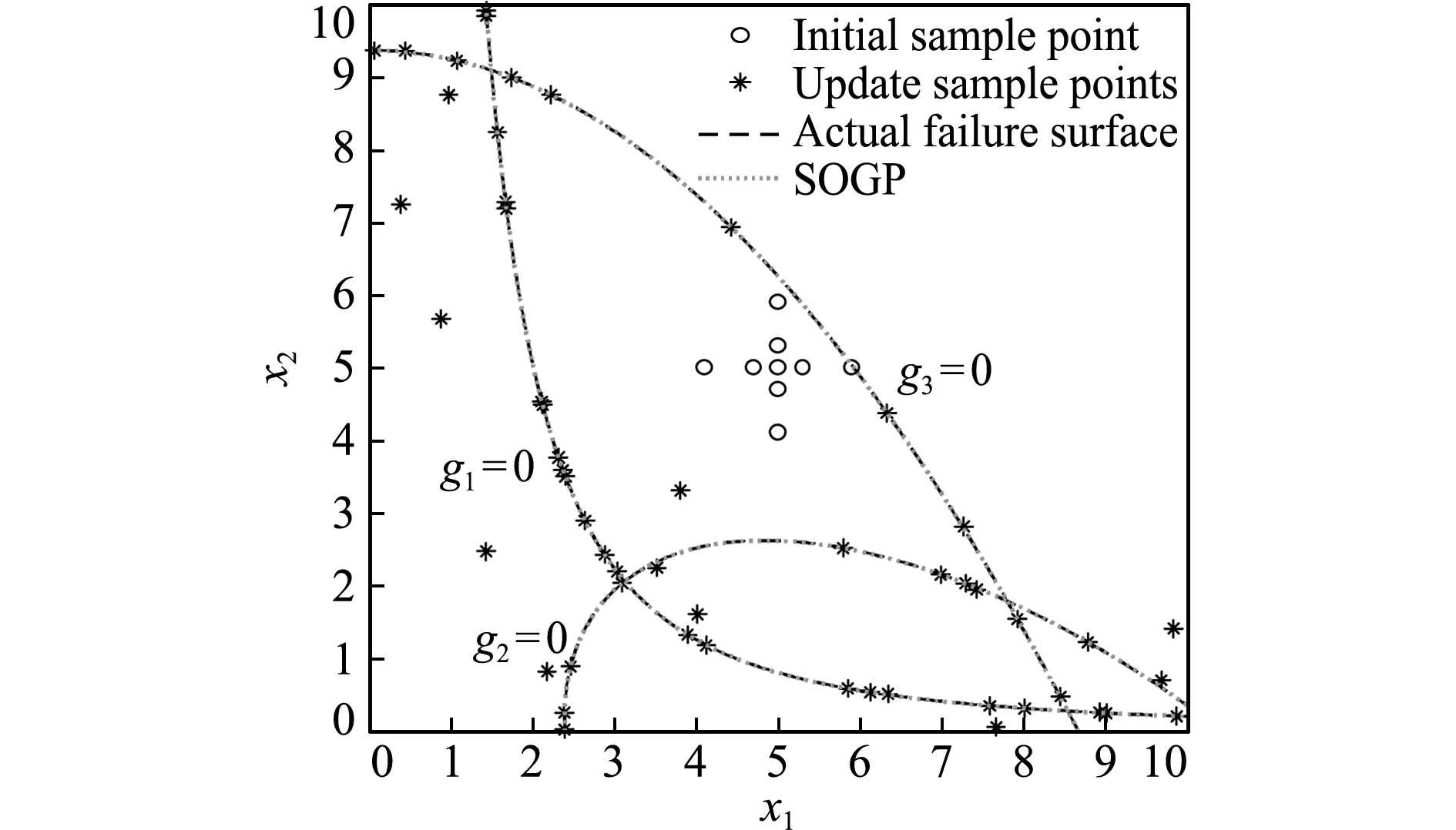
图4 算例1的SOGP模型(训练样本-1)
Fig.4 SOGP of example 1(training samples -1)
RBDO问题求解。利用训练后的MOGP模型进行RBDO问题求解,算例1的计算结果列入 表1。可以看出,当设计变量服从不同分布时,基于MOGP模型三种优化算法的计算结果与文献[14,15]的计算结果几乎一致,说明本文方法具有较好的近似精度。在计算效率方面,本文方法需调用真实模型45次(初始样本点为9个,后续训练模型共增加了36个样本点),而文献方法需调用真实模型约130~200次,表明本文方法的计算效率较好。
算例2具有3个概率约束的RBDO问题,其中极限状态1与2并联,然后二者与极限状态3串联,定义为
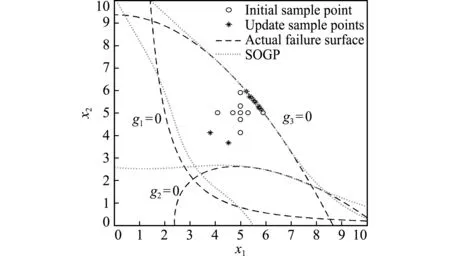
图5 算例1的SOGP模型(训练样本-2)
Fig.5 SOGP of example 1(training samples-2)
表1 算例1的计算结果
Tab.1 Calculation results of example 1
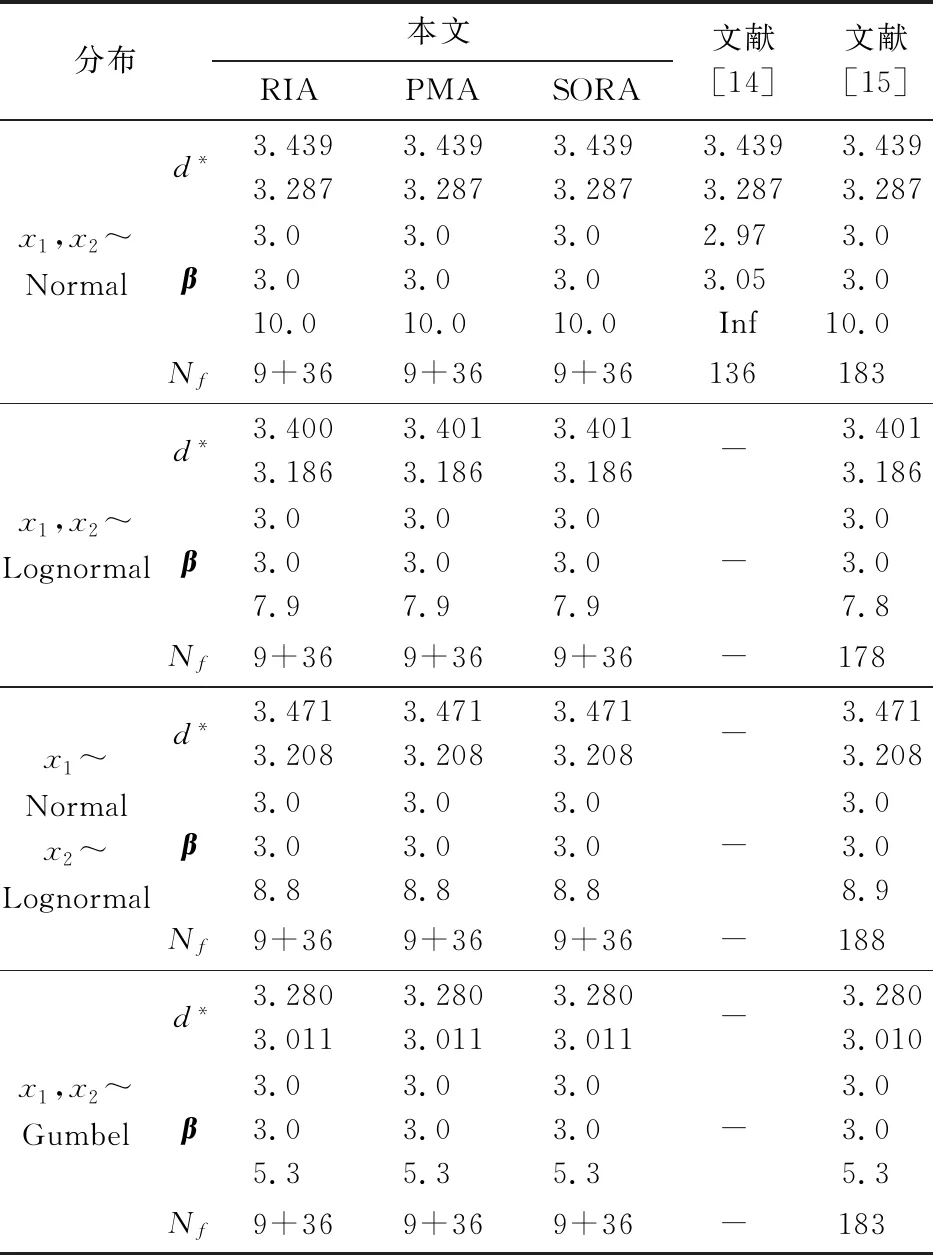
分布本文RIAPMASORA文献[14]文献[15]x1,x2~Normald*3.4393.2873.4393.2873.4393.2873.4393.2873.4393.287β3.03.010.03.03.010.03.03.010.02.973.05 Inf3.03.010.0Nf9+369+369+36136 183 x1,x2~Lognormald*3.4003.1863.4013.1863.4013.186 -3.4013.186β3.03.07.93.03.07.93.03.07.9 -3.03.07.8Nf9+369+369+36 -178 x1~Normalx2~Lognormald*3.4713.2083.4713.2083.4713.208 -3.4713.208β3.03.08.83.03.08.83.03.08.8 -3.03.08.9Nf9+369+369+36 -188 x1,x2~Gumbeld*3.2803.0113.2803.0113.2803.011 -3.2803.010β3.03.05.33.03.05.33.03.05.3 -3.03.05.3Nf9+369+369+36 -183
min.f(d)=(μx1-3)2+(μx2+1)2
s.t.Pfj(g(x)<0)≤Φ(-βT),βT=3.0
g2(x)=2-x1-8x2
g3(x)=(x1+3)2+(x2+3)2-4
-5.0≤μxi≤5.0σxi=1 (i=1,2)
(11)
算例3具有7个相互独立的正态设计变量和11个串联概率约束的RBDO问题[14,16]定义为式(12)。
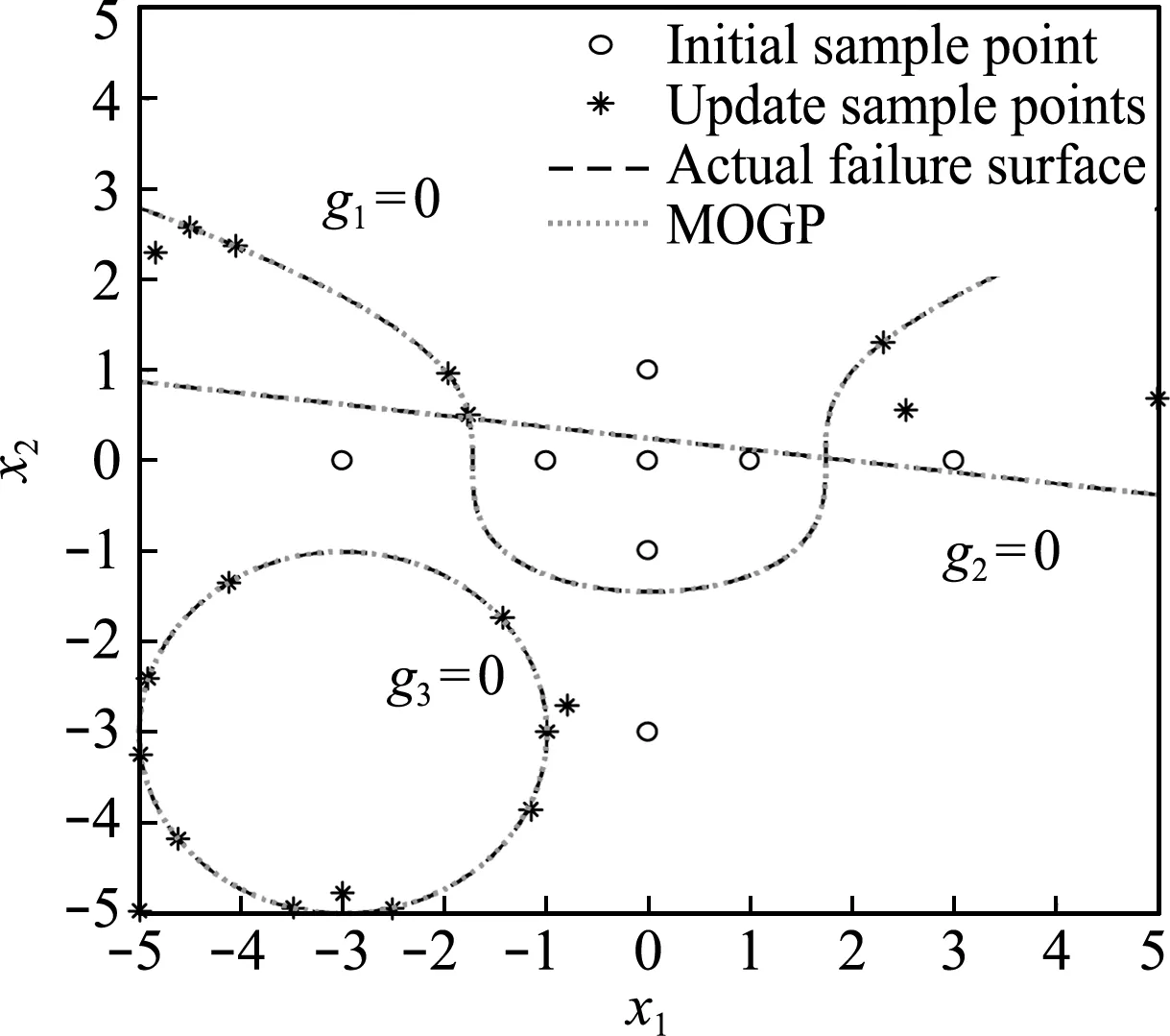
图6 算例2的MOGP模型
Fig.6 MOGP of example 2
表2 算例2的计算结果
Tab.2 Calculation results of example 2
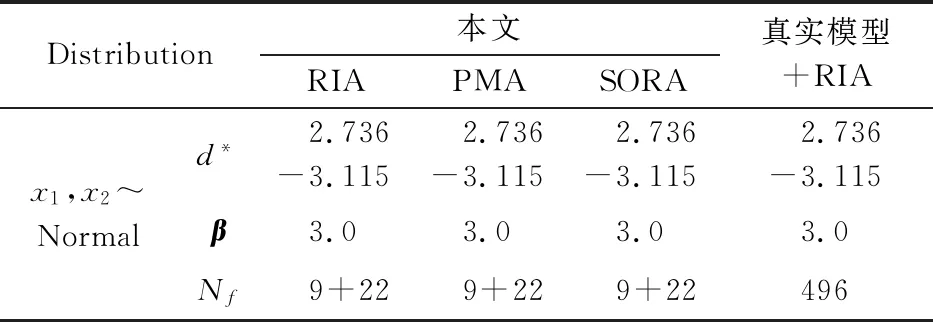
Distribution本文RIAPMASORA真实模型+RIAx1,x2~Normald*2.736-3.1152.736-3.1152.736-3.1152.736-3.115β3.0 3.0 3.0 3.0 Nf9+229+229+22496
g7(x)=x2x3-40,g8(x)=5-x1/x2
g9(x)=x1/x2-12
g10(x)=(1.56x6+1.9)/x4-1
g11(x)=(1.1x7+1.9)/x5-1
2.6≤μx1≤3.6, 0.7≤μx2≤0.8
17≤μx3≤28, 7.3≤μx4≤8.3
7.3≤μx5≤8.3, 2.9≤μx6≤3.9
5.0≤μx7≤5.5σxi=0.005 (i=1,2,…,11)
(12)
表3 算例3的计算结果
Tab.3 Calculation results of example 3

本文RIAPMASORAd*3.5765,0.7000,17.0000,7.3000,7.7537,3.3652,5.3017βInf,Inf,Inf,Inf,3.013,3.002,Inf,3.003,Inf,Inf,2.956Nf29+91d*3.5764,0.7000,17.0000,7.3000,7.7538,3.3652,5.3017βInf,Inf,Inf,Inf,2.993,3.015,Inf,2.986,Inf,Inf,2.956Nf29+91d*3.5765,0.7000,17.0000,7.3000,7.7538,3.3652,5.3017βInf,Inf,Inf,Inf,3.018,3.005,Inf,3.001,Inf,Inf,2.956Nf29+91文献[14]d*3.5765,0.7000,17.0000,7.3000,7.7541,3.3652,5.3017βInf,Inf,Inf,Inf,3.000,3.000,Inf,3.001,Inf,Inf,3.000Nf514文献[16]d*3.580,0.700,17.000,7.300,7.764,3.366,5.302βInf,Inf,Inf,Inf,3.14,3.08,Inf,3.14,Inf,Inf,4.23Nf627
6 结 论
(1) 本文方法首先利用Bucher方法生成初始样本并构建初始MOGP模型,然后采用均匀布点的方法生成训练样本,并利用学习函数对初始MOGP模型进行不断训练。由于训练样本均匀遍布整个设计空间,利用学习函数能够在大范围内筛选出较为满意的训练样本,从而使得MOGP模型具有较好的全局精度。
(2) MOGP模型本身考虑了输出矢量可能存在的相关性,即针对多个极限状态函数只需一次模型构建,无需对每个极限状态函数分别建立代理模型,对多输入多输出系统具有良好的预测性能。
(3) 本文方法先构建MOGP模型,待MOGP模型构建完成后,再利用构建后MOGP模型进行基于可靠性的结构优化。即在整个优化过程中无需重新构建MOGP模型,且代理模型的构建不受结构可靠度以及优化算法的限制。数值算例表明,本文方法的计算结果与文献方法几乎一致,且本文方法的计算效率要明显优于文献方法,尤其是设计变量数目与失效模式数目较多时效率提升明显。
