互补问题算例分析

雍龙泉

（陕西理工学院数学与计算机科学学院，陕西汉中723001）

互补问题算例分析

雍龙泉

（陕西理工学院数学与计算机科学学院，陕西汉中723001）

给出了互补问题的测试算例，研究了这些算例的特征，为互补问题算法的研究提供了测试平台。

线性互补；非线性互补；正定矩阵；唯一解；多个解

衡量求解互补问题算法的优劣，需要根据相应数值实验的测试结果做出判断。数值实验要求所给互补问题的解是已知的，通过对比测试结果和已知解就能知道算法的优劣，因此，设计一些能够反映互补问题的测试算例是该领域的一个重要研究课题。在本文中，笔者给出了一些互补问题的测试算例，并分析了这些算例的特性，为互补问题的研究提供了测试平台。

1 线性互补问题常用的算例

定义1［1］：若对任意的 x∊ℝn，都有 xΤMx ≥0，则矩阵 M∊ℝn×n称为半正定矩阵；若对任意的 x∊ℝn，x≠ 0 ，都有 xΤM x＞0，则M称为正定矩阵。

当M是半正定矩阵时，称相应的LCP为单调线性互补问题。

引理1［1］：设矩阵 M∊ℝn×n是一个半正定矩阵，若对于任意 q∊ℝn，LCP是可行的，则LCP必有解，且解集为凸集。

引理2［1］：设矩阵 M∊ℝn×n是一个正定矩阵，则对于任意 q∊ℝn，LCP有唯一解。

上述判定线性互补问题解存在的条件是充分条件，而非必要条件。

下面给出一些常见的线性互补问题的测试算例［2-3］。

1.1 矩阵M正定且对称的线性互补问题的算例

算例1：考虑线性互补问题，其中

通过计算可知，矩阵M的特征值分别为λ1= 0.308 0，λ2= 0.643 1， λ3=5.048 9。由于特征值全为正值，故矩阵M是正定矩阵。由引理2可知，该线性互补问题的解是唯一存在的，且该唯一解为 x*=(0,4,3)。Τ

算例2：考虑线性互补问题，其中

由于矩阵M是一个三对角矩阵，通过计算可知其特征值全大于零，矩阵M是正定矩阵。由引理2可知，该线性互补问题的解是唯一存在的。另外，该问题的解具有对称性。

算例3：考虑线性互补问题，其中

通过计算可知，矩阵M的特征值全大于零，故矩阵M是正定矩阵。由引理2可知，该线性互补问题的解是唯一存在的，且唯一解为 x*=(1,0,… ,0)Τ。

算例4：考虑线性互补问题，其中

算例2、算例3和算例4可以用来测试算法求解的精度。

1.2 矩阵M正定且非对称的线性互补问题的算例

算例5：考虑线性互补问题，其中

通过计算，可求得M的特征值为λ1=1.438 4，λ2= 5.561 6， λ3= λ4= 4。由于特征值全为正值，故矩阵M是正定矩阵。由引理2可知，该线性互补问题的解是唯一存在的，且唯一解为 x*=(1,0,1,0)Τ。

算例6：考虑线性互补问题，其中

容易验证， M∊ℝn×n是正定矩阵。由引理2可知，该线性互补问题的解是唯一存在的，且唯一解为x*=(0,0,… ,0,1)Τ。该算例可以用来测试算法求解的精度。

下面的算例说明，矩阵的特征值为复数时，矩阵也可能是正定或半正定矩阵，因此特征值非负是M正定或半正定的充分而非必要条件［3］。

算例7：考虑线性互补问题，其中

经过计算可得矩阵M的特征值分别为 λ2=1，λ2= 2.2225，λ3= 0.8888+ 1.8054i，λ4= 0.8888- 1.8054i。由于特征值中存在复数，故不能用特征值来判断矩阵M的正定性。

算例8：考虑线性互补问题，其中

经过计算可知，矩阵M的特征值为λ1= 0.264 0+ 5.298 0i， λ2= 0.264 0 - 5.298 0i ，λ3= 0.7487 +2.5437i，λ4= 0.748 7 - 2.543 7i，λ5= 0.174 3 +1.888 8i，λ6= 0.174 3 -1.888 8i，λ7=0.625 9。

醌类化合物是中药中一类具有醌式结构的化学成分，广泛存在于动植物和矿物中，以蒽醌类居多，萘醌和苯醌类次之，且大多具有重要的生物活性。

由于特征值中存在复数，故不能用特征值来判断正定性，下面用定义来判别矩阵M的正定性。

1.3 矩阵M非正定的线性互补问题的算例

算例9：考虑线性互补问题，其中

经过计算可知，矩阵M的特征值为λ1= λ2= 0.5+ 0.866i，λ3= λ4= 0.5 -0.866i。由于特征值都是复数，故只能用定义来判别矩阵M的正定性。

算例10：考虑线性互补问题，其中

经过计算可知，M的特征值为 λ1=17.326 9，λ2= 1.386 2，λ3= 3.758 9，λ4= 9.100 3，λ5= 0.2138+ +1.6091i；λ6= 0.2138 -1.6091i。由于特征值中存在复数，故只能用定义来判别矩阵M的正定性。

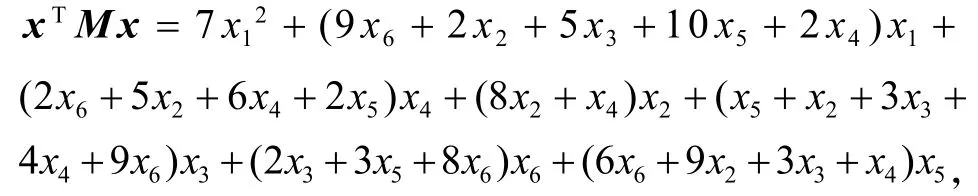
对于任意的 x=(x1, x2, x3, x4, x5, x6)Τ。由于若取=(0,0,0,0, -8,3)Τ，则有因此矩阵M不是正定矩阵，但是该问题具有唯一解x*=(0.7,0,0.3,0,0.6,0)Τ。

经过计算可知，M的特征值为 λ1= 4.4665，λ2= -4.466 5，λ3= 0.223 9，λ4=-0 .2239， λ5=0。由于存在负特征值，故矩阵M是非半正定矩阵。

把上述算例的结果进行归纳，可得表1。

关于线性互补问题，常见的求解方法是针对单调线性互补问题的，而非单调的线性互补问题（即矩阵M非半正定）方面的研究较少，算例9～11可以用来测试算法的适用范围，即对非单调的线性互补问题，算法是否适用。

表1 线性互补算例特征分析

1.4 无解的线性互补问题的算例

下面给出无解的线性互补问题的算例［4–6］。

算例12：考虑线性互补问题，其中

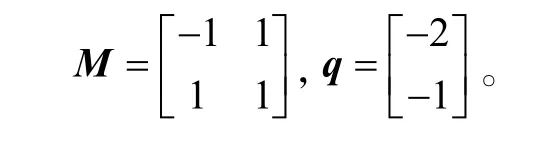
算例13：考虑线性互补问题，其中

经过计算可以发现以上线性互补问题无解。

能否在算法终止时判别有解或无解，可以用算例12和算例13进行测试。

1.5 含参数的线性互补问题的算例

下面给出含参数的线性互补问题的算例［7］。

算例14：考虑线性互补问题，其中

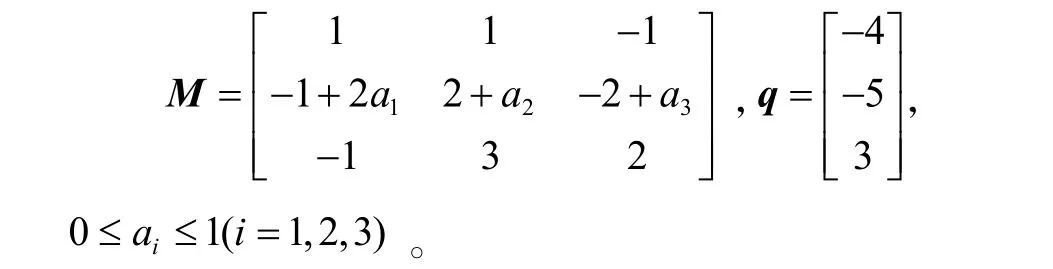
经过计算可得，该问题的唯一解为

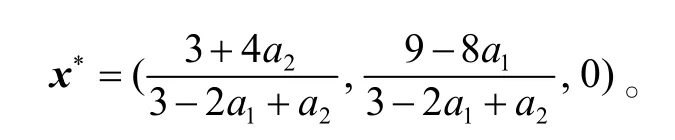
算例15：考虑含参数的线性互补问题，其中

经过计算可得，该问题的唯一解为

算例16：考虑线性互补问题，其中

经过计算可得，该问题的唯一解为

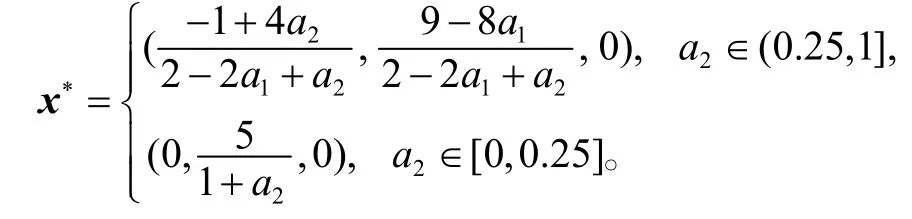
算例14～16常用于算法的灵敏度分析。

2 非线性互补问题常用的算例

文献［1］详细地给出了非线性互补解存在的条件。下面仅给出常见的非线性互补算例，这些算例在有变分不等式的互补问题中经常用到［8–10］。

2.1 有唯一解的非线性互补问题的算例

算例17：考虑非线性互补问题，其中

该非线性互补问题的唯一解为 x*=(1,1,0)Τ。算例18：考虑非线性互补问题，其中

该非线性互补问题的唯一解为 x*=(2,1,0)Τ。算例19：考虑非线性互补问题，其中

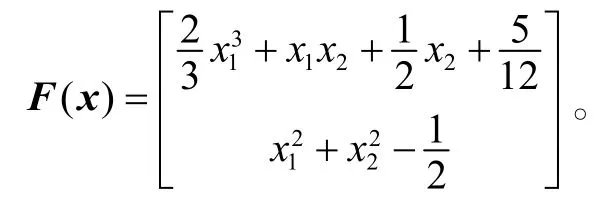
算例20：考虑非线性互补问题，其中

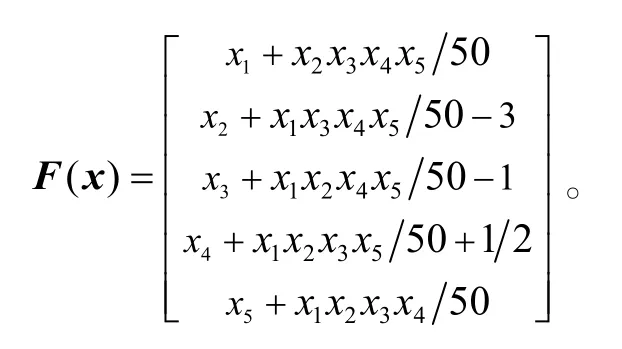
该非线性互补问题的唯一解为 x*=(0,3,1,0,0)Τ。

2.2 有多个解的非线性互补问题的算例

算例21：考虑非线性互补问题，其中

该问题的非退化解为 x*=(1,0,3,0)Τ，退化解为

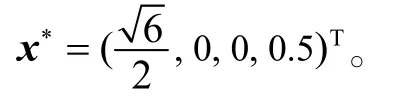
算例22：考虑非线性互补问题，其中

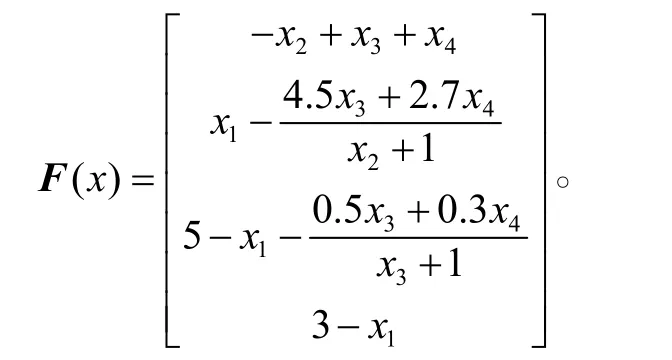
该问题有无穷多个解 x*=(λ,0,0,0)Τ，其中λ∊[0,3]。

3 结束语

在本文中，笔者详细地给出了互补问题的一些测试算例，在验证互补问题算法的有效性时，可以通过这些算例验证算法的优劣。

［1］ 韩继业，修乃华，戚厚铎.非线性互补理论与算法［M］.上海：上海科学技术出版社，2006：31-125.

［2］ 雍龙泉，邓方安，陈涛.单调线性互补问题的一种内点算法［J］.数学杂志，2009（5）：681-686.

［3］ 雍龙泉，邓方安.线性互补问题中矩阵正定性判别的两点注记［J］.吉首大学学报（自然科学版），2009（1）：33-35.

［4］KOSTREVAM M，WIECEKM M.Linear Complementarity Problems and Multiple Objective Programming［J］. Mathematical Programming，1993，60:349-359.

［5］ISAC G，KOSTREVA M M，WIECEK M M.Multiple Objective Approximation of Feasible but Unsolvable LinearComplementarityProblems［J］.JournalofOptimization Theory and Applications，1995，86:389-405.

［6］KOSTREVA M M，YANG X Q.Unified Approaches for Solvable and Unsolvable Linear Complementarity Problems［J］.European JournalofOperationalResearch，2004，158:409-417.

［7］ XIAO B C.The Linear Complementarity Problem with a Parametric Input［J］.European Journal of Operational Research，1995，81:420-429.

［8］ JIANG H Y，QI L Q.A New Nonsmooth Equations Approach to Nonlinear Complementarity Problems［J］. Siam Journal on Control and Optimization，1997，35: 178-193.

［9］ 屈彪，王长珏，张树霞.一种求解非线性互补问题的方法及其收敛性［J］.计算数学，2006（3）：247-258.

［10］雍龙泉.基于多目标优化算法求解非线性互补问题［J］.中南大学学报（自然科学版），2011（增刊1）：596-599.

【责任编辑 王云鹏】

Examp le Analysis for Com p lementary Problem

YONG Longquan
（School ofMathematics and Computer Science，ShanxiUniversity of Technology，Hanzhong 723001，China）

Complementary problem test examples were given in the paper，and the characteristic of these examples were studied respectively，which provided a test platform on algorithm for complementary problem.

linear complementarity；nonlinear complementarity；positive definitematrix；unique solution；multiple solutions

O221

A

2095-7726（2015）06-0004-05

2015-02-10

国家自然科学基金项目（11401357）；陕西理工学院教学改革研究项目（SLGYJG1416）

雍龙泉（1980-），男，陕西洋县人，副教授，博士，研究方向：最优化理论与算法、智能优化算法。