近场脉冲地震下自复位中心支撑钢框架结构抗震性能评估
2020-01-04孙国华
王 琪, 孙国华, 魏 鑫
(苏州科技大学 土木工程学院,江苏 苏州215011)
通过在抗弯钢框架结构中增设中心支撑可显著提高结构的整体抗侧刚度及水平承载力,降低梁柱连接节点的弯矩,简化节点构造[1-2]。 目前,在多高层工业及民用建筑中,钢框架中心支撑结构(简称CBF)已得到广泛应用[3]。 但是,传统钢框架中心支撑结构在遭受强烈地震时,中心支撑易发生整体失稳,承载力退化迅速,震后结构出现较大残余变形,已有研究表明当结构震后层间残余位移角超过0.5%时,结构修复成本会超过重建成本[4-5],修复难度也会增加。 因此,一些学者致力于具有震后复位功能的新型结构体系的研究,提出了自复位中心支撑钢框架结构[6]。 刘璐[7]分别对普通抗弯钢框架、防屈曲支撑钢框架和自复位防屈曲支撑钢框架进行了弹塑性时程分析,研究证实了自复位防屈曲支撑钢框架结构震后残余变形最小、复位效果最佳。郑锦铜等[8]为验证自复位中心支撑框架结构(简称SC-CBF)的复位效果,设计了一个单层、单跨、足尺SCCBF 平面试件,并进行了低周往复加载试验,试验结果表明SC-CBF 结构获得了旗帜型滞回曲线,具有良好的复位功能。 Mojtaba Dyanati 等[9]采用有限元软件对具有相同配置的CBF 和SC-CBF 结构进行弹塑性时程分析, 对比了两种结构的层间变形和层间残余位移角, 分析结果进一步证实了SC-CBF 结构可实现震后复位。Can-Xing Qiu 等[10]将具有自复位功能的阻尼器布置于钢框架中,并对其进行了Pushover 分析和弹塑性时程分析,结果表明自复位阻尼器能显著降低抗弯钢框架结构的震后残余变形。
结合已提出的SC-CBSF 结构弹塑性层剪力分布模式和理想屈服机构[11],引入最大有效滞回耗能谱(简称MECE)[12],提出了基于能量平衡原则可考虑近断层速度脉冲影响的SC-CBSF 结构的抗震设计方法。 本文主要对文献[1]设计的2 个具有不同目标延性系数的5 层SC-CBSF 结构进行弹塑性时程分析,评估了SCCBSF 结构在罕遇地震作用下的变形及震后复位效果。
1 算例设计
1.1 算例概况
设计了2 个SC-CBSF 结构算例,设防烈度为8 度(0.3g),场地类别为Ⅱ类,地震分组为第一组。 算例编号分别为SC-CBSF-1、SC-CBSF-2。 其中,算例SC-CBSF-1 的设计目标延性系数μt=2,算例SC-CBSF-2 的设计μt=4。算例跨度及柱距均为6 000 mm,层高3 600 mm。中跨钢梁与钢柱之间铰接,边跨钢梁与钢柱刚接,柱脚为刚接。 钢材强度等级为Q345B。 算例的平面及立面布置见图1 和图2。

图1 5 层 3 跨 SC-CBSF 算例的平面布置(mm)
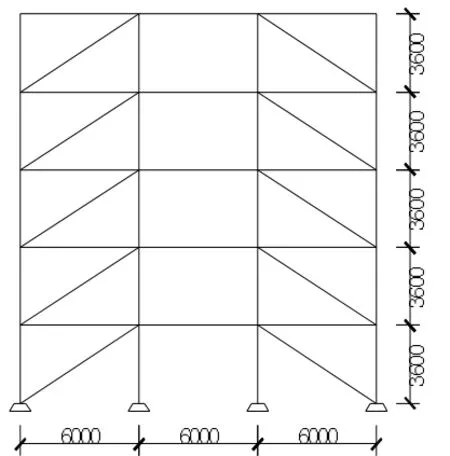
图2 5 层 3 跨SC-CBSF 算例的立面布置(mm)
采用基于MECE 谱的抗震设计方法所确定的2 个5 层SC-CBSF 结构的钢梁、 钢柱和自复位SMA 钢支撑的截面见表1 与表2 所列。

表1 算例SC-CBSF-1 的钢梁、柱和支撑截面

表2 算例SC-CBSF-2 的钢梁、柱和支撑截面
1.2 自复位SMA钢支撑的滞回性能
为确保分析有效性,算例采用的自复位SMA(Shape Memory Alloys, SMA)钢支撑的滞回准则,见图3。 σMS为SMA 支撑的屈服应力;σMf为SMA 支撑的马氏体相变结束应力;σAS为SMA 支撑的奥氏体相变开始应力;σAf为SMA 支撑的恢复应力;εL为SMA 支撑的最大相变应变;E 为SMA 支撑的等效弹性模量。
图4 给出了SC-CBSF 算例所采用自复位SMA 钢支撑在低周往复荷载作用下的滞回曲线。 由图4 可知,基于所采用的滞回准则可实现自复位SMA 钢支撑的旗帜型滞回特征,可用于模拟自复位SMA 钢支撑的滞回性能。
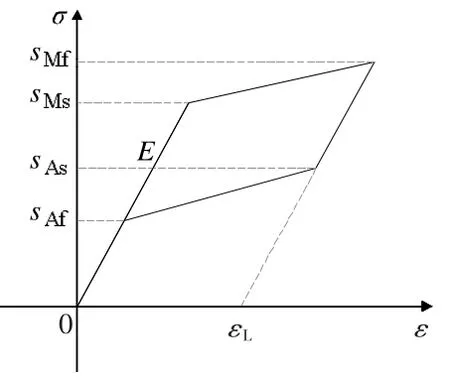
图3 SMA 钢支撑的滞回特征
1.3 算例SC-CBSF的滞回性能
图5 给出了SC-CBSF 算例在循环Pushover 作用下的基底剪力(P)-顶点位移角(Δ/H)滞回曲线[1]。 由图5 可知,在文献[1]中,基于 MECE 谱设计的 2 个 SCCBSF 算例的滞回曲线均具有较为理想的旗帜型特征。
图6 给出了SC-CBSF 算例在循环Pushover 作用下最大层间变形的层间剪力(Vi)-层间位移角(δ/h)滞回曲线[1]。 由图6 可知,SC-CBSF 算例在结构层间位移角达到2%时,其卸载后残余层间位移角均小于0.5%。 这说明基于MECE 谱法设计的2 个SC-CBSF 算例均实现了良好的复位功能。
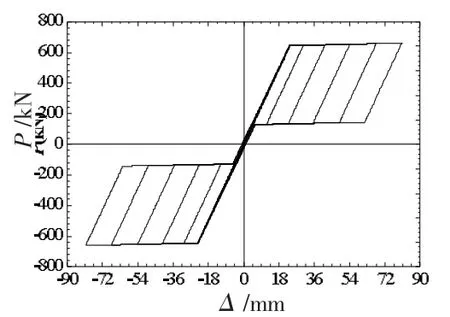
图4 SMA 钢支撑的滞回曲线
2 近场地震波及最大有效滞回耗能的计算
2.1 近场速度脉冲地震波的特性

图5 SC-CBSF 算例的整体滞回曲线

图6 SC-CBSF 算例的层间滞回曲线(第二层)
大多数研究人员普遍认可距离断层破裂面不超过20 km 的范围称为近断层区域,近断层区域的地震动一般具有明显的高能量速度脉冲运动特性。通常情况下,引起速度脉冲的因素一般有方向性效应、滑冲效应、上盘效应和强竖向地震动等,其中以方向性效应和滑冲效应最为主要,这种高能量脉冲地震动一般会对结构产生严重的破坏。
图7 给出了一条典型近场速度脉冲地震波的加速度、速度和位移时程曲线。图7 进一步证实了近场速度脉冲地震波所携带的能量通常集中在一二个强速度脉冲中,往往会导致结构出现过大的地震响应,造成严重的损伤。
2.2 算例SC-CBSF的最大有效滞回耗能
通常将近场速度脉冲地震波的速度时程曲线中所对应t1至t2之间所携带的能量作为最大有效滞回耗能,见图8。 因此,本文通过对SC-CBSF 结构进行弹塑性时程分析,选取较大速度脉冲时段内的结构层间剪力-层间位移曲线的包络面积作为最大有效滞回耗能。 SC-CBSF 结构的最大有效滞回耗能取所有楼层最大有效滞回耗能的叠加。
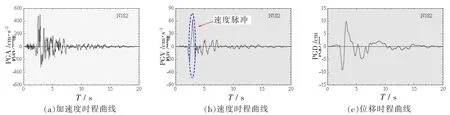
图7 典型的近场速度脉冲地震波
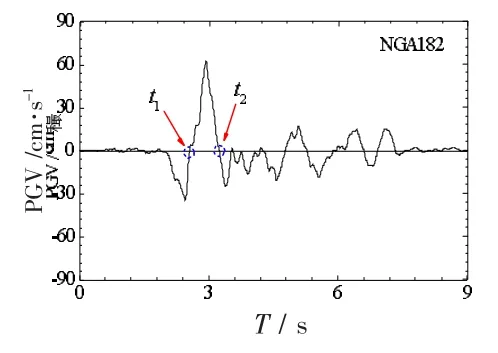
图8 最大有效滞回耗能的计算
2.3 近场速度脉冲地震波的选取
目前,关于近场速度脉冲地震波的合理选取尚无明确标准。 翟长海[14]建议参考PGV/PGA 比值选取近场速度脉冲地震波。 韦韬[15]认为速度脉冲的持时、波形及峰值是判断近场速度脉冲地震波的重要条件。 为确保近场速度脉冲地震波选择的合理性,本文采用如下选波原则:
(1)震中距不大于20 km;
(2)速度时程曲线具有较大脉冲波形;
(3)罕遇地震水准,单条近场速度脉冲地震波作用下SC-CBSF 结构计算的最大有效滞回耗能值与基于能量平衡法的最大有效滞回耗能设计值误差不超过35%;
(4)罕遇地震水准,所选择的10 条近场速度脉冲地震波作用下SC-CBSF 结构计算的最大有效滞回耗能平均值与基于能量平衡法的最大有效滞回耗能设计值近似相等。
根据上述原则,分别针对2 个SC-CBSF 算例筛选出两组近场速度脉冲地震波。 其中,每组均为10 条近场速度脉冲地震波,见表3 与表4 所列。
两个SC-CBSF 算例对应于罕遇地震水平下基于弹塑性时程方法所得到的最大有效滞回耗能见图9。 由图9 可知, 由于地震波的随机性,4 个SC-CBSF 算例对应于罕遇地震作用下基于弹塑性时程方法所得到的最大有效滞回耗能具有一定的离散性,但误差均控制在35%范围之内。 算例SC-CBSF-1、SC-CBSF-2 基于MECE 谱的能量设计值分别为245.89 kN·m、198.96 kN·m, 这和基于弹塑性时程方法所得到的最大有效滞回耗能平均值误差分别为7.87%、-0.26%,误差均较小。因此,本文筛选的2 组近场速度脉冲地震波可以用来评估SC-CBSF 结构的抗震性能。
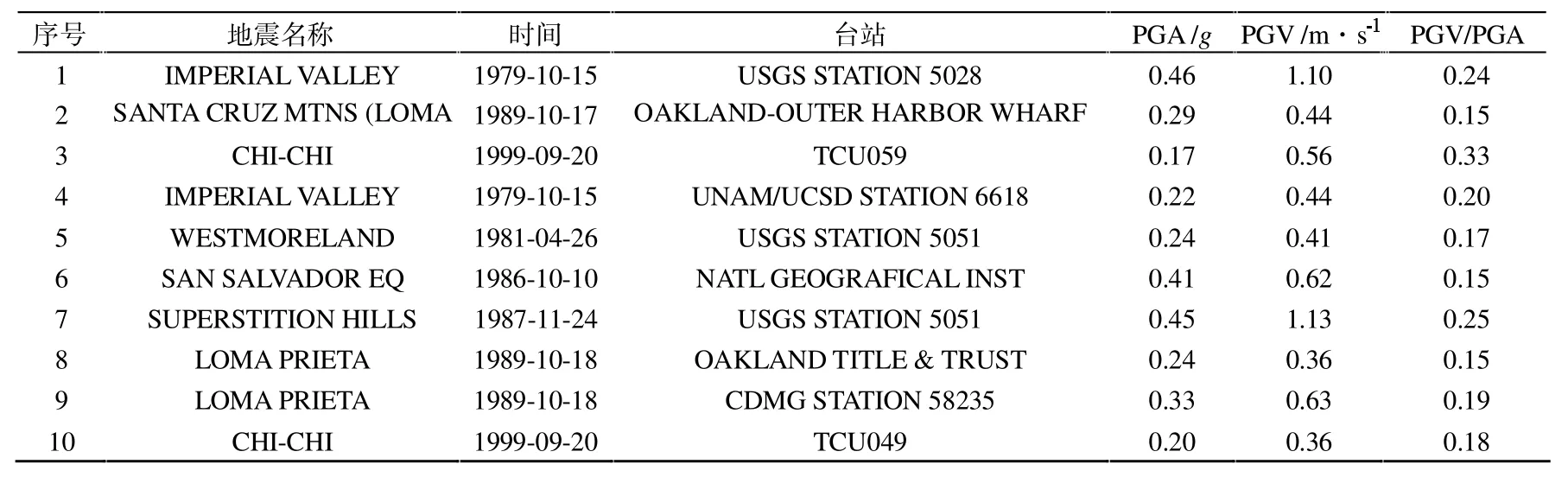
表3 算例SC-CBSF-1 的近场速度脉冲地震波
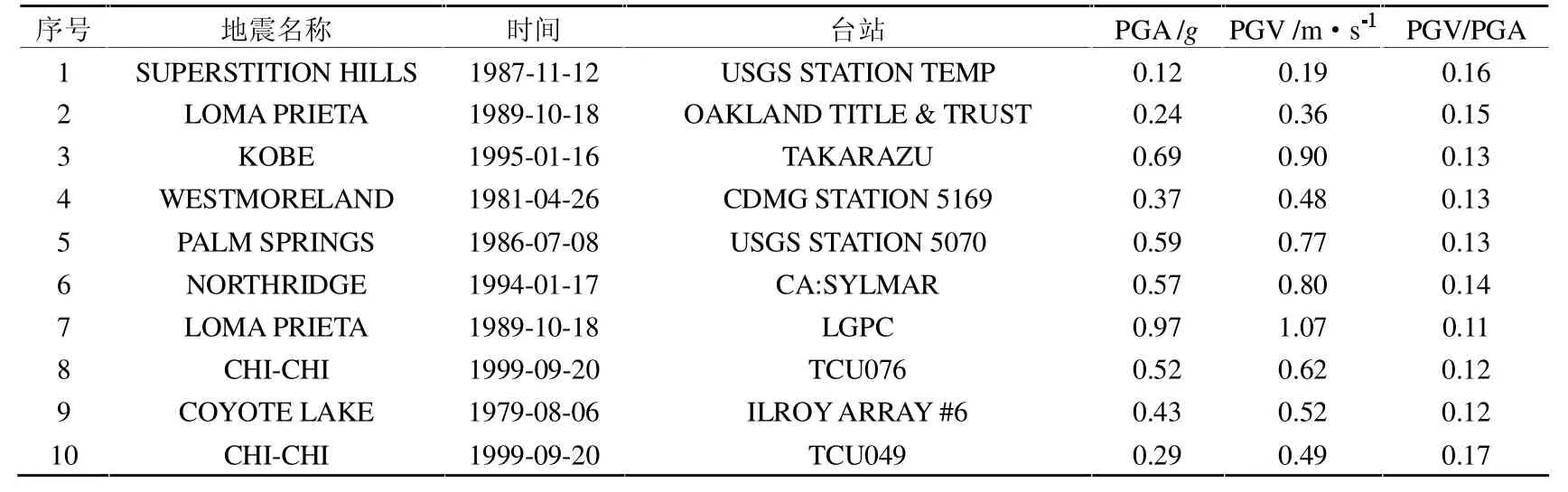
表4 算例SC-CBSF-2 的近场速度脉冲地震波
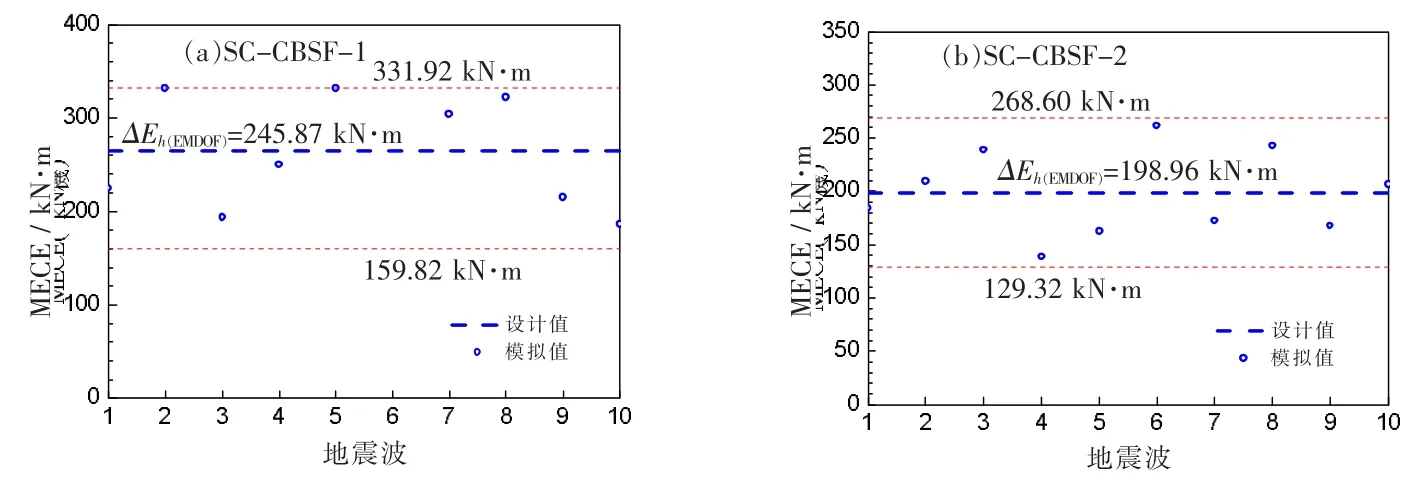
图9 SC-CBSF 算例的最大有效滞回耗能
3 SC-CBSF结构的抗震性能评估
采用弹塑性时程方法获得了2 个SC-CBSF 算例在近场速度脉冲地震作用下的楼层位移、 残余楼层位移、层间位移角及残余层间位移角,依据分析结果评估了2 个SC-CBSF 算例在罕遇地震作用下的抗震性能及损伤后的复位效果。
3.1 SC-CBSF结构楼层位移
图10 给出了2 个SC-CBSF 算例在近场速度脉冲地震作用下的最大楼层位移(Δmax)。由图10 可知,由于地震波的随机性导致SC-CBSF 算例在罕遇地震作用下的楼层位移均具有较大的离散性。在结构高度相同情况下,按目标位移延性系数μt=4 设计的算例SC-CBSF-2 楼层位移明显大于按μt=2 设计的算例SC-CBSF-1结构楼层位移。 因此,在罕遇地震下,μt越大,SC-CBSF 结构楼层位移越大,所受地震影响越明显。
3.2 SC-CBSF结构的残余楼层位移
图11 给出了2 个SC-CBSF 算例在近场速度脉冲地震作用下的残余楼层位移δres。 由图11 可知,由于算例SC-CBSF-1 的构件截面略大,致使在结构高度相同情况下,算例SC-CBSF-1 的残余楼层位移明显小于算例SC-CBSF-2 的残余楼层位移。 总体上,2 个算例在近场罕遇地震激励结束后的残余楼层位移均较小。
3.3 SC-CBSF结构的层间位移角
图12 给出了2 个SC-CBSF 算例在近场速度脉冲地震作用下的层间位移角(IDRmax)。由图12 可知,算例SC-CBSF-1、SC-CBSF-2 的最大层间位移角均出现在第三层, 其均值分别为0.9%、1.84%, 这与基于MECE谱设计时采用的层间位移角限值1.06%、2.12%较为接近。两个SC-CBSF 算例的层间位移角沿高度分布趋于均匀,表明结构的非弹性性能沿楼层分布较均匀,各楼层可耗散相当的地震能量。两个SC-CBSF 算例的相对薄弱层出现在结构中部,底层和顶层的层间位移角略小,这是底层约束较强及顶层受到地震响应略小所致。

图10 SC-CBSF 算例的楼层位移
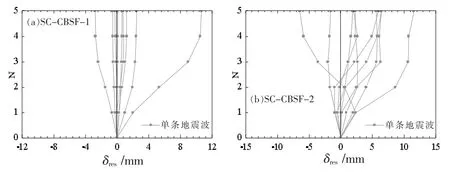
图11 SC-CBSF 算例的残余楼层位移
3.4 SC-CBSF结构的残余层间位移角
图13 给出了2 个SC-CBSF 算例在近场速度脉冲地震作用下的残余层间位移角(RIDR)。 由图13 可知,2 个SC-CBSF 算例的最大残余层间位移角均出现在第3 层,这与其最大层间位移角所在楼层相同,其均值分别为0.02%、0.06%,远小于0.5%限值。 算例SC-CBSF-1 在部分近场速度脉冲地震波作用下的残余层间位移角基本为零。 因此,在罕遇地震作用下,基于MECE 谱法设计的2 个SC-CBSF 算例具有理想的复位能力。
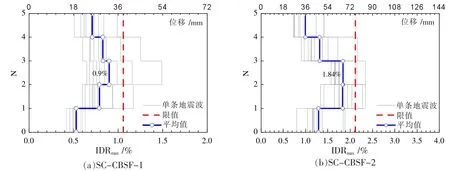
图12 SC-CBSF 算例的层间位移角

图13 SC-CBSF 算例的残余层间位移角
4 结论
采用弹塑性时程方法评估了文献[1]基于考虑近场速度脉冲效应的MECE 谱法设计的2 个SC-CBSF 算例的抗震性能,主要得出以下结论:
(1)在结构高度相同情况下,算例SC-CBSF-2 楼层位移明显大于算例SC-CBSF-1 结构楼层位移。因此,目标延性系数越大,SC-CBSF 结构楼层位移越大,所受地震影响越明显。
(2)2 个SC-CBSF 算例的薄弱层均出现在结构第三层,底层和顶层层间位移角较小,这主要由于底层所受约束较强及顶层所受地震响应略小所致。 层间位移角基本和基于MECE 谱法设计时采用的层间位移角限值比较接近。
(3)2 个SC-CBSF 算例具有较大的抗侧能力,其残余层间位移角都小于0.5%,具有理想的震后复位能力。
(4)基于弹塑性时程方法证实了基于MECE 谱的能量抗震方法设计SC-CBSF 结构的可靠性。
