基于变形场测量数据主元压缩的模型参量反求方法
2020-05-22李建宇张丽丽魏凯杰
李建宇,任 朝,张丽丽,魏凯杰
(1.天津科技大学 机械工程学院,天津市轻工与食品工程机械装备集成设计与在线监控重点实验室,天津 300222;2.天津职业技术师范大学 理学院,天津 300222)
1 引 言
模型参量反求是一种利用试验测量数据反求力学模型中的未知参量的方法。对于涉及多个物理参数的复杂力学模型,如复合材料和弹塑性等,模型参量反求技术是获取模型参数的有效手段,近年来受到研究者的关注[1]。De wilde等[2]较早地提出结合数值计算与试验测量来反求材料参量的方法。Ghouati等[3]采用集成有限元和优化技术的方法来测量材料参数。国内学者在模型反求算法方面也开展了系统而深入的工作[4-6]。
目前,数字图像相关DIC(Digital Image Correlation)技术[7]的发展已经使得对结构变形信息的全场测量成为可能,不仅为直接观测结构的力学响应提供了便利,也为利用变形测量信息进一步研究结构和材料的物理性能提供了数据支撑。将DIC测量数据与模型参量反求技术结合并应用于具体工程问题的研究受到关注,如马源等[8]对风电叶片的弹性参数进行了反求,杨思满等[9]研究了车用复合材料的参数反演问题。
DIC测量技术的发展有效解决了结构变形数据获取的问题,但是如何更有效地使用DIC变形数据又成为新的问题。由于数字图像包含的数据量极大,如果在模型参量反求中使用全部的测量数据,不仅会导致计算耗时长及收敛速度慢等问题,而且也没有必要。现有文献还很少有关于如何有选择性地使用部分DIC数据进行力学模型参量反求的研究。已有的工作多采用均匀抽样的方法从测量数据中间隔抽取离散的数据点[10,11]进行计算,这种做法的问题是数据点之间的间距不好把握。倘若间隔过大,则抽取数据量少,无法确保较为全面地获得测量场的主要信息,这在具有变形奇异的问题中较为突出,如非标准几何形状铝板的变形[12]和剪切带的滑移问题[13],数据量太少容易丢失局部信息;反之,若间隔过小,则抽取数据量增加,又为后续反求计算带来困难。
在图像识别和机器学习领域[14],常采用数据压缩的手段来处理大数据问题。海量数据经数据压缩后,虽然存在一定的信息损失,但压缩后的数据却能够保持原数据的主要特征。目前,常用的数据压缩技术有主元分析法、局部保持投影法和拉普拉斯特征投影法等[14],其中主元分析法是最基本的线性数据压缩方法。本文针对DIC测量数据量庞大和选点困难的问题,提出采用基于主元分析的数据降维方法对DIC数据进行压缩处理,并在此基础上给出一种模型参量反求方法。一方面,确保DIC变形场测量的重要特征不会因压缩而丢失;另一方面,有助于显著节省数据存储和计算时间。
2 基于主元分析的DIC测量数据压缩
2.1 DIC测量简介
在各种非接触全场光测力学方法中,DIC以其具有实验设备及测量过程简单、环境适应性强、测量精度高和适用范围广等优势得到了广泛应用,已经作为一种常用而有效的表面变形测量手段应用于实验固体力学领域[13,15]。
DIC测量的基本原理是匹配物体表面不同状态下的数字化散斑几何点,追踪点的运动得到物体表面的变形信息。散斑场上的散斑是随机分布的,将每个散斑点周围的小区域称为子区域。散斑场上以某一点为中心的子区域可作为该点位移的载体,通过搜索和分析该子区域的移动和变化,便可获得该点的位移。如图1所示,以特征点P为中心的参考区域S为子区域,其大小为m×n个像素,当发生运动后,子区域S移动到子区域S1的位置,由此可以得到特征点P变形后的位置P1,从而得到P点的位移。对于高质量的散斑图,DIC的位移测量精度可达到0.01像素,图像数据量在十万级以上,极其庞大。

图1 特征点P的位移
Fig.1 Displacement of characteristic pointP
2.2 DIC测量位移数据的主元分析
主元分析PCA(Principal Component Analysis)的基本原理是从数据中识别主要特征,将高维数据通过线性变换投影到低维空间,再通过特征值分析,确定需要保留的主元个数,实现数据的压缩。主元分析经常作为一种数据集预处理技术,在数据应用到其他算法之前使用,能够去除冗余信息和噪声,使数据变得更加简单高效,提高计算效率。但是,将主元分析技术用于压缩DIC测量数据并用于力学模型的参量反求的研究还鲜有报道。
给定一DIC测量位移场,包括m×n个测点,其中m为测点行数,n为测点列数。所测量位移构成二维矩阵Um n,如式(1)。
(1)
式中列向量
ui=[u1i…um i]T(i=1,…,n) (2)
利用主元分析方法对式(1)所示的位移场进行压缩处理,具体步骤如下。
(1) 数据中心化处理
(3)
式中 mean为按列计算均值、repmat为将矩阵mean(Um n)复制m×1块。
(2) 协方差矩阵特征值分解
(4)
式中Φ为特征向量,λ为特征值。
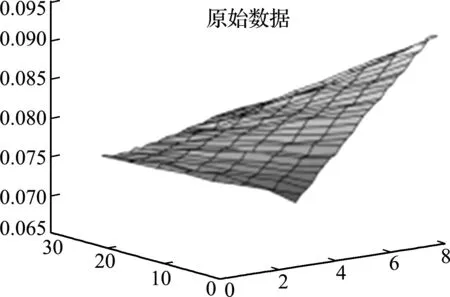
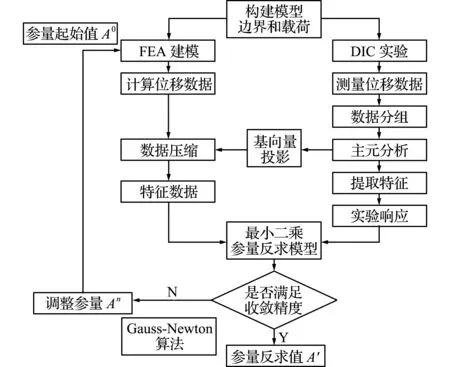
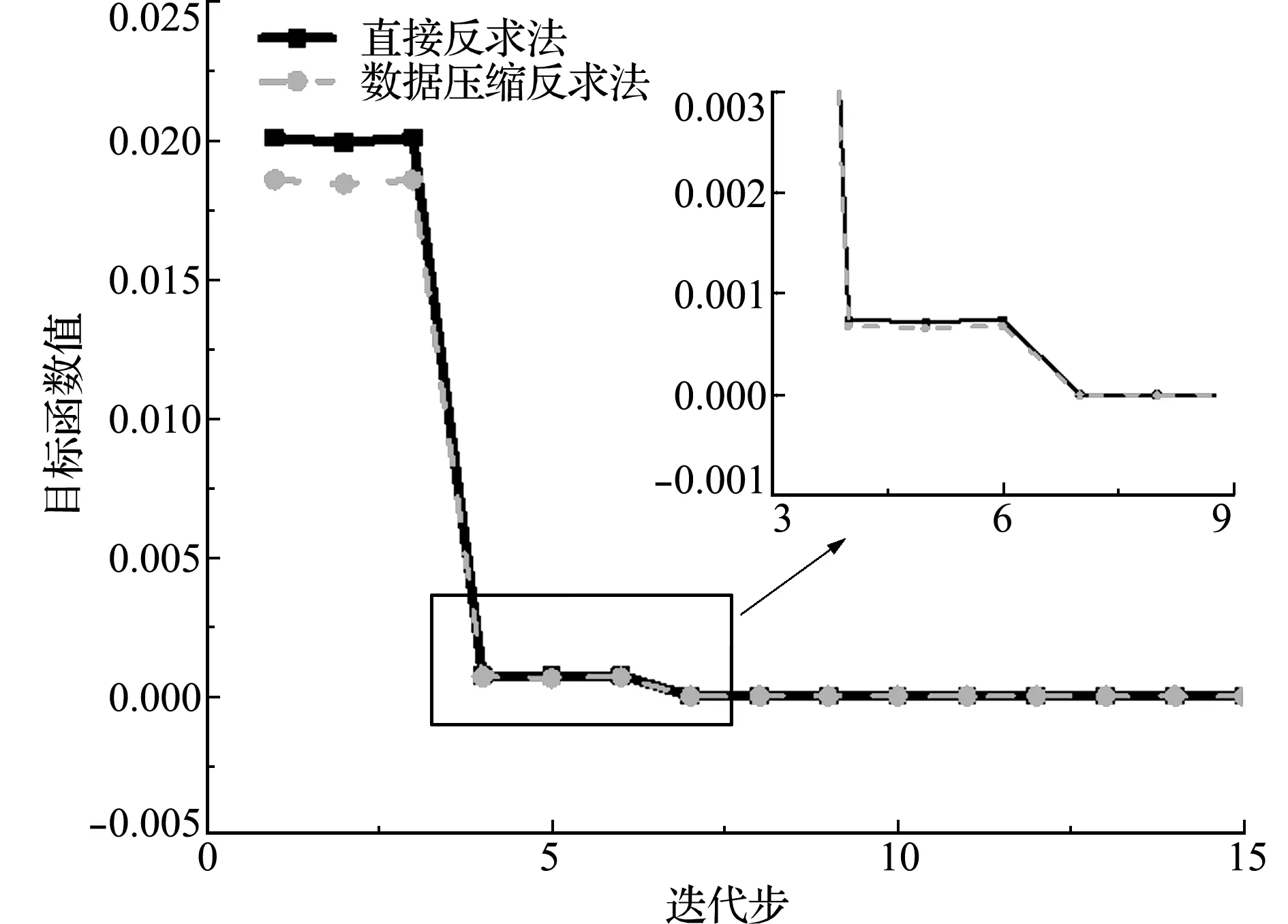
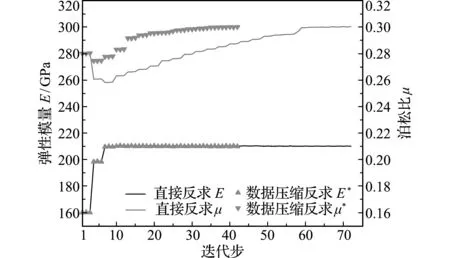
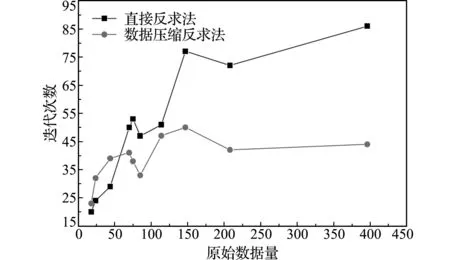
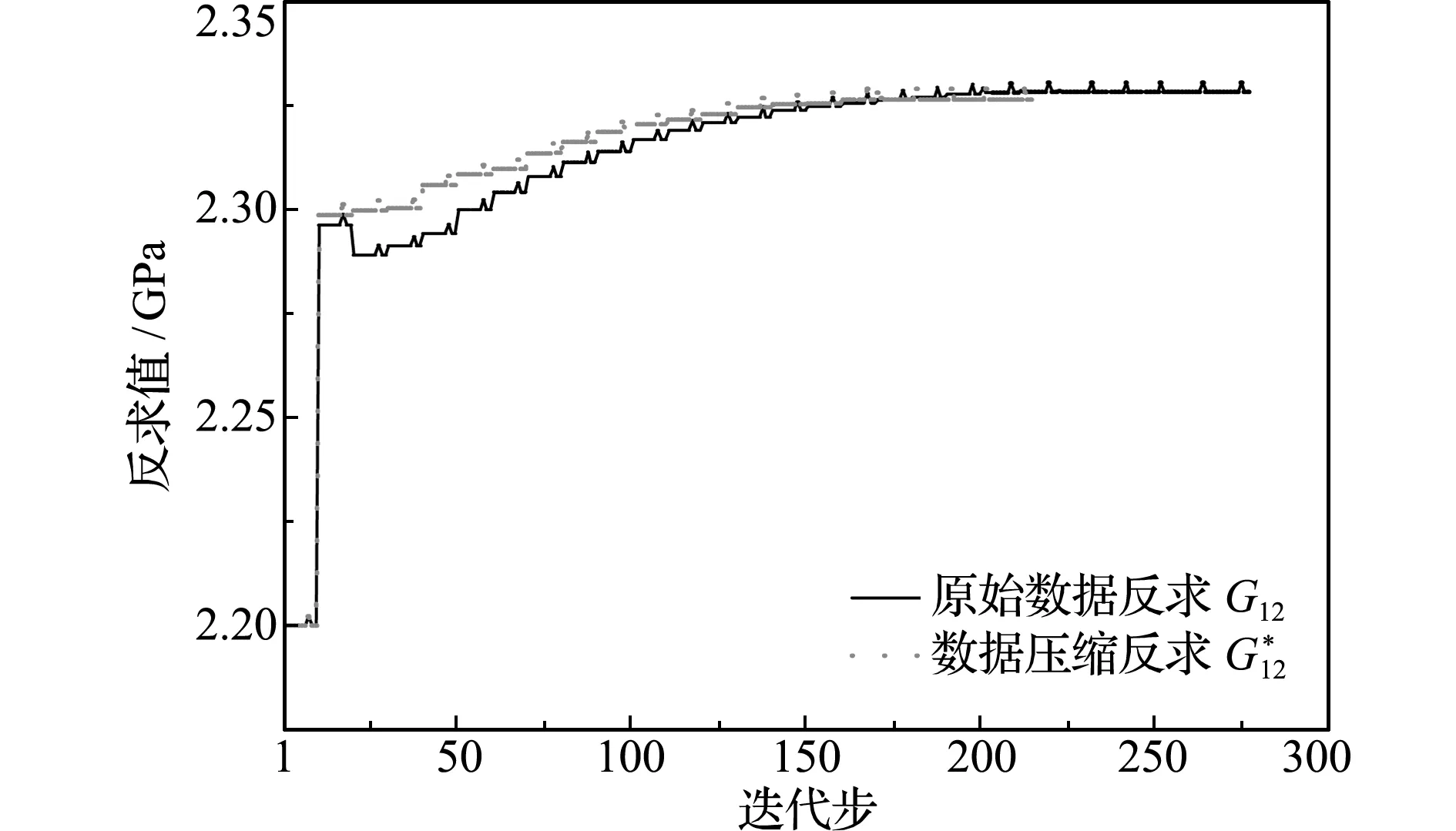
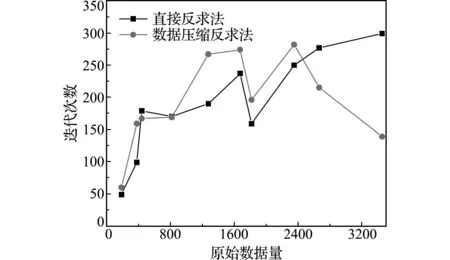
(3) 数据压缩,截取前r (5) (6) 累计方差解释率[16]: (7) r的取值通常要使得累计方差解释率达80%以上,从而保证包含原始数据的主要信息特征。 利用上述PCA方法对DIC测量位移数据进行压缩处理。试验采用MTS E45万能试验机和美国CSI公司的DIC仪器。DIC仪器能最高处理55000个节点数据,包括2个400万像素的CCD相机、2个照明光源和Vic -3D测量系统。数据采集过程如图2所示,设定测量区域,设置子区为 29 pixel×29 pixel,步长为7 pixel,在试件测量平面内选择208个数据点采集位移信息。 图2 DIC数据采集过程 Fig.2 DIC data acquisition process 对于设定的测量区域,位移信息可以用一个二维矩阵表示,以铅垂方向的位移分量为例,表面测点数据为26×8,利用主元分析对该数据矩阵进行压缩处理,选择第一主元(26×1)即能满足精度要求。数据量由208个降低为26个。图3为原始数据和第一主元表征数据的三维形貌对比。 综上所述,位移数据通过PCA压缩后具有以下特征。 (1) 存储数据规模降低,原始数据维数由m×n压缩为m×r。对于结构变形问题,数据矩阵的主要信息集中在前几个主元,r取值1~3即能满足累计方差解释率大于0.8的要求。 (2) 处理后的数据更趋于平滑,具有降噪的功能,可有效消除测量误差的影响。 利用最小二乘法进行模型参量反求的基本数学模型为 (8) 式中A为待求的模型参量,uC(A)为模型计算位移值,uM为实际测量位移值。在上述模型中,测量数据的选择对于模型参量的反求计算影响甚大。若选择的数据点个数过多,容易导致计算耗时长和收敛速度慢的问题;若选取的数据点数量偏少,可能导致信息丢失和过拟合等问题。为此,本文提出一种基于数据PCA压缩的模型参量反求方法。 图3 原始数据和第一主元表征数据的三维形貌对比 Fig.3 Comparison of three -dimensional morphology between original data and first principal component characterization data 对数据进行PCA处理在实质上是将原始数据在一组正交基向量{Φj}构成的坐标系统中进行投影展开,即μi在基向量Φj上的投影坐标为zi j。而压缩的含义为通过截取前几阶特征值较大的分量来近似逼近原始数据。因此,将直接采用测量数据转为通过比较实测数据与模型计算数据在{Φj}上的投影坐标值{zi j}来实现模型参量的反求。进一步,经PCA数据压缩后,仅需比较前几阶坐标投影值,就可减少目标函数项数。基于该思路,在最小二乘法的框架下,构建如下模型参量反求模型。 (9) 式中 zC r(A)=uC(A)Φ,uC(A)=zC r(A)ΦT 进入10月下旬,随着南方最后一小部分地区秋季肥扫尾工作的顺利结束,全国的秋季肥市场也彻底画上了句号。从现阶段开始,到11月冬储政策发布之前,市场将会处在短暂的空档期。目前复合肥主流出厂报价:45%氯基复合肥在2000-2200元/吨,45%硫基复合肥在2300-2500元/吨。 (10) zM r=uMΦ,uM=zM rΦT (11) Φ=[Φ1…Φr],Φj=[Φj1…Φj n]T (j=1,…,r) (12) (13) 由式(10,11),根据PCA截断原理[16] (14) 式中 第一个等式为PCA全项正交展开,第二个约等号为PCA截取前r阶特征。再利用{Φj}的正交性得 (15) 模型参量反求模型的求解,目前主要包括两类算法,一类为基于梯度的局部优化算法,如Gauss-Newton法[17]和L-M算法等;另一类为基于智能进化的全局优化算法,如蚁群算法、遗传算法和粒子群法等。本文采用Gauss-Newton法求解式(8,9),其中梯度值采用差分法计算。Gauss-Newton法对初值较为敏感,计算过程中所选的初值应该在解的附近。考虑到本文研究是利用实验数据反求模型参数,在计算过程中选用所研究材料参数的标称值为初值,这在一定程度上保证了初值与解相距不远。图4给出基于数据PCA压缩的模型参量反求流程。 选取碳素结构钢Q235和纤维复合材料层合板作为试验对象,应用万能试验机进行单轴拉伸试验和三点弯曲试验。通过DIC测量试验过程中的位移信息,反求材料的弹性模量和泊松比等参数[15,18]。 针对金属材料拉伸试验的模型参量反求,在有限元软件中进行参量化建模,模型如图5所示。设定初始材料参数弹性模量E和泊松比μ,边界条件为一端固定,另一端施加位移载荷,单元类型为C3D8I(8节点三维实体,非协调单元),根据网格大小确定数据量,采集平面内的全场数据点,获取金属材料在拉伸过程的位移信息。 在选择原始数据量大且累计方差解释率高的208个数据量时,图6给出了直接反求法和数据压缩反求法的结果对比,图7展示了两个材料参数的迭代过程。可以看出,目标函数值下降较快,本文所提模型(9)的目标函数值和待求模型参量均逼近经典模型(8)的目标函数值和待求参量值。 试验表明,直接反求法和数据压缩反求法的迭代过程呈现较大差异。从图8可以看出,随数据量的增大,本文方法的收敛迭代次数较直接反求法的迭代次数明显减少。而且,本文方法的收敛迭代次数不会随着数据量的增加而显著增加,而是趋于稳定。 图4 模型参量反求流程 Fig.4 Flow chart of inverse of model parameters 图5 Q235拉伸试件 Fig.5 Q235 tensile testspecimen 结果表明,经多次迭代计算,数据PCA压缩的模型参量计算反求方法实现了反求值快速收敛于参考值,相较直接反求法,两者获得待识别的材料参数都具有较高精度。 针对复合材料三点弯曲试验的模型参量反求,加入需要反求的参数形式。在有限元软件中的模型及参数如图9所示,其中E11,E22和E33分别为11,22和33方向的弹性模量;G12,G13和G23分别为12,13和23方向的剪切模量;μ12,μ13和μ23为泊松比。设定初始材料参数,边界条件为下端两侧铰支,上端施加位移载荷,单元类型为C3D8R(8节点三维实体,缩减积分单元),根据单元尺寸确定采集平面内的全场数据量,获取复合材料在三点弯曲过程的位移信息。 图6 两种方法的目标函数值对比(208个原始数据) Fig.6 Comparison of objective function by two methods(208 data) 图7 2个材料参数迭代过程对比(208个原始数据) Fig.7 Comparison of iterative process of two material parameters (208 data) 图8 数据量对迭代次数的影响 Fig.8 Effects of data volume on iteration times 在选择原始数据量大且累计方差解释率高的2667个数据下,图10给出直接反求法和数据压缩反求法的结果对比。图11展示了其中四个材料参数的迭代过程。可以看出,目标函数值下降较快,本文模型(9)的目标函数值和待求模型参量均逼近经典模型(8)的目标函数值和待求参量值。 试验表明,直接反求法和数据压缩反求法的迭代过程呈现较大差异。图12给出了随数据量增大,直接反求法与数据压缩反求法的迭代次数对比。可以看出,随数据量的增大,本文方法的收敛迭代次数较直接反求法的迭代次数明显减少。 图9 复合材料三点弯曲试样 Fig.9 Composite three -point bending testspecimen 结果表明,在识别九个复合材料参数时,基于PCA数据压缩的计算反求方法对多个未知材料参数在较大区间下具有较强的识别能力,且反求的精度和速度均较为理想。 在DIC测量中,图像噪声引起的随机误差对系统的正常工作有着很大的影响[19],有必要对方法的抗噪声性能进行分析。为此,本文直接在数值模型的基础上考察噪声对所提方法的影响。依据Vic-3D的测量误差在100 μm范围内,在理论计算位移数据中添加均值为0、方差σ=100 μm的高斯随机噪声,分析直接反求法和基于数据PCA压缩的模型参量反求算法在引入噪声下的反求效果。 图10 两种方法的目标函数值对比(2667个原始数据) Fig.10 Comparison of objective function by two methods(2667 data) 图11 4个材料参数迭代过程对比(2667个原始数据) Fig.11 Comparison of iterative process of four material parameters (2667 data) 试验表明,对比无噪声结果,在引入噪声的情况下,基于数据PCA压缩的模型参量反求算法的结果精度变化更小。同时,对比直接反求,在有无噪声情况下,本算法的迭代次数均明显较小,呈现出更快的收敛速度、更强的稳定性和抑噪能力。 图12 数据量对迭代次数的影响 Fig.12 Effects of data volume on iteration times 本文提出一种基于变形场测量数据PCA压缩的模型参量反求算法,以解决DIC测量数据量庞大导致的数据使用困难。算法采用测量平面内全场性和无序性的数据点,通过PCA压缩数据,选择满足累计方差解释率的主元信息进行反求,确保DIC位移测量的重要特征不会因压缩而丢失。 针对具体的试验模型,研究表明,基于数据PCA压缩后的模型参量反求适用于多个参数的反求,并具有较高精度和较好稳定性。特别是与直接反求法相比较,本文方法具有更快的收敛速度和更高的收敛精度,在处理噪声方面,该方法具有降噪和去冗余的能力,能有效降低噪声的影响。2.3 试验分析

3 基于数据PCA压缩的模型参量反求方法


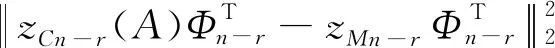
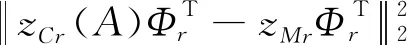
4 算 例
4.1 金属材料拉伸试验
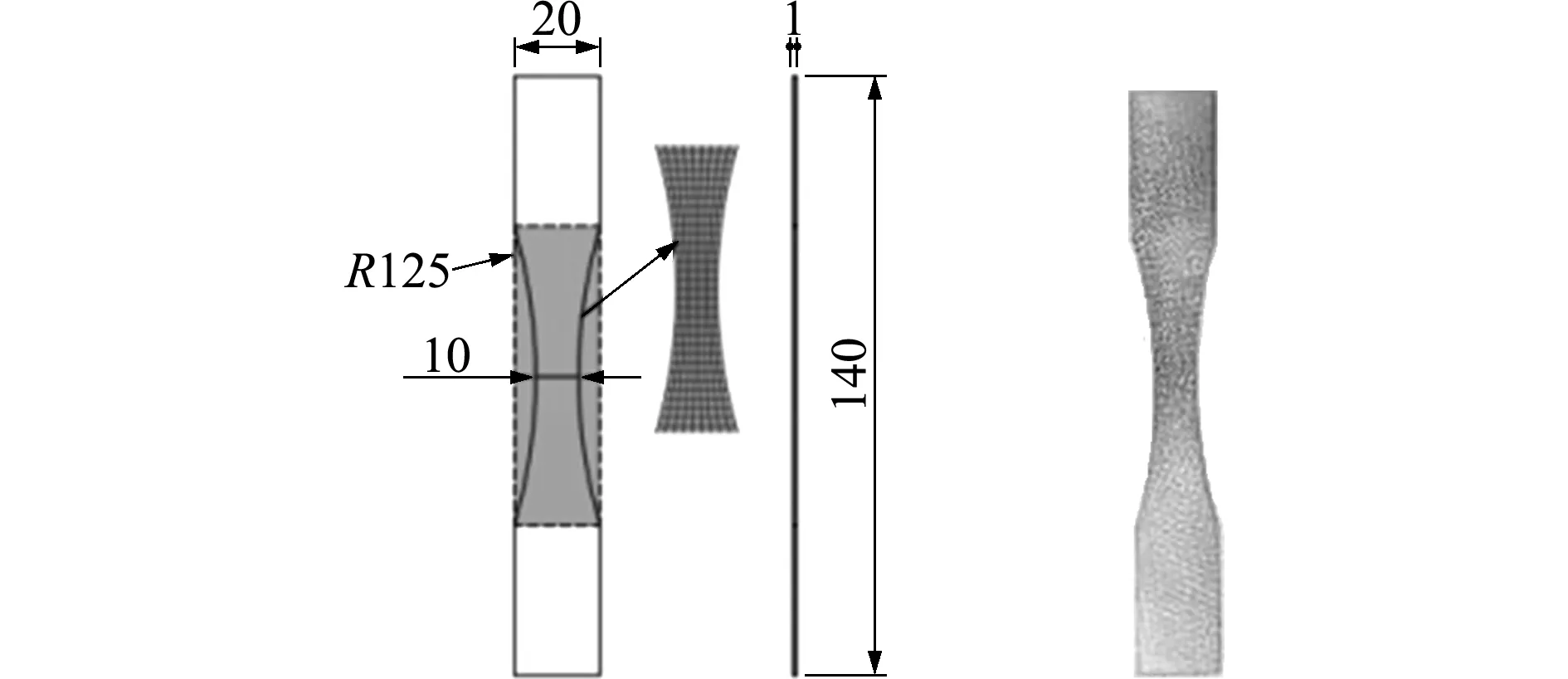
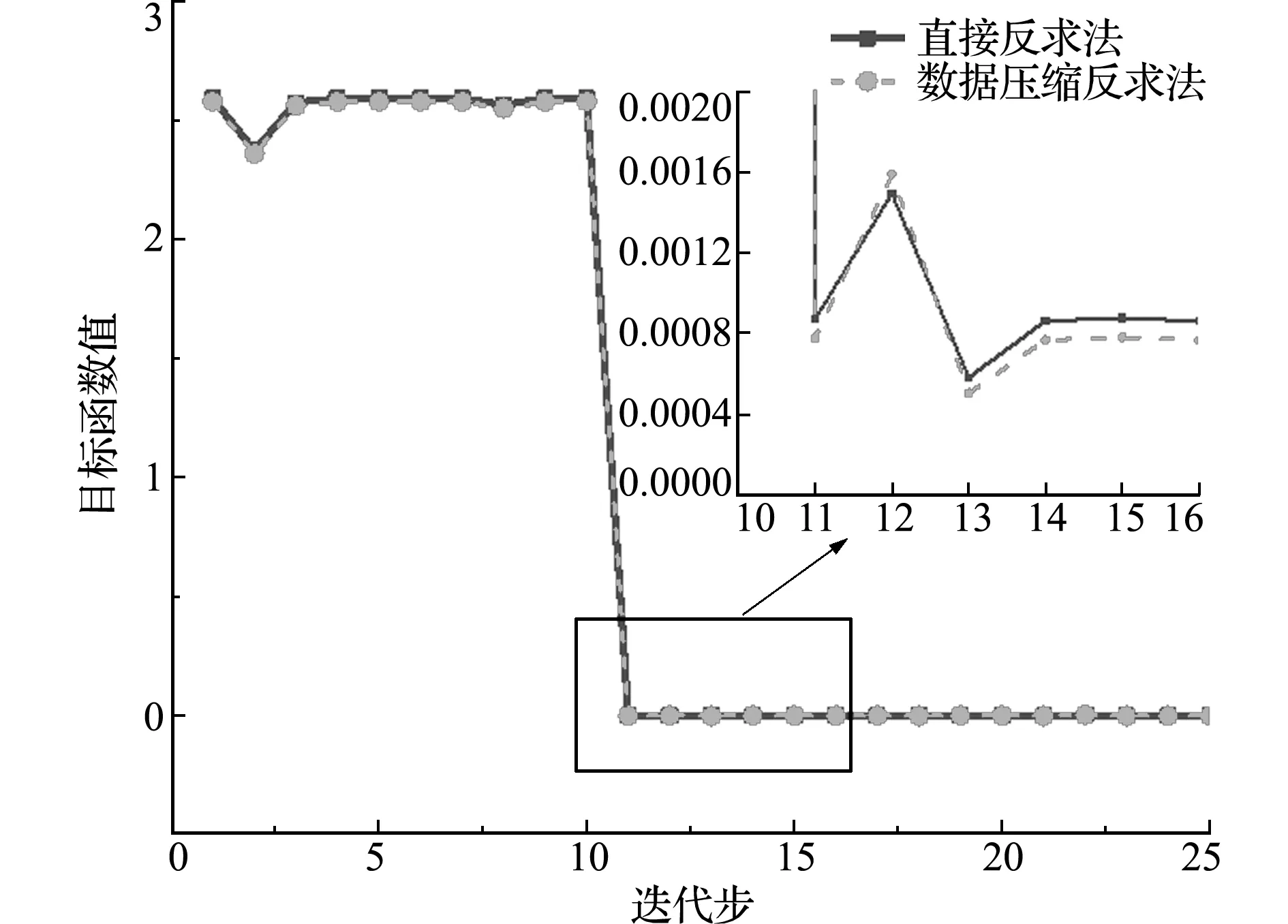
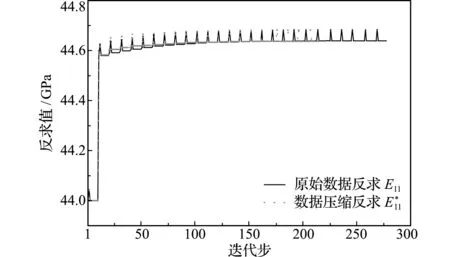
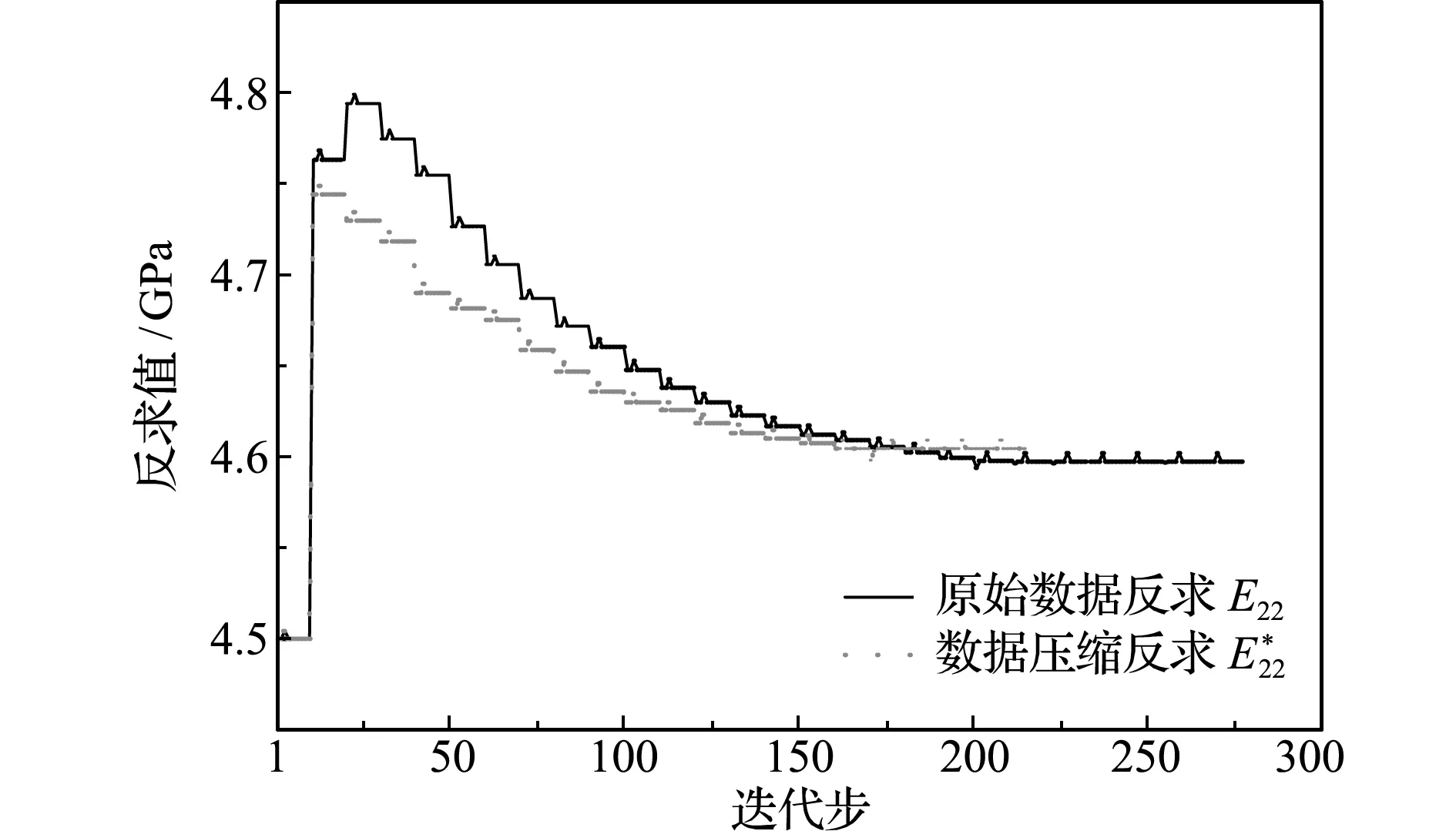
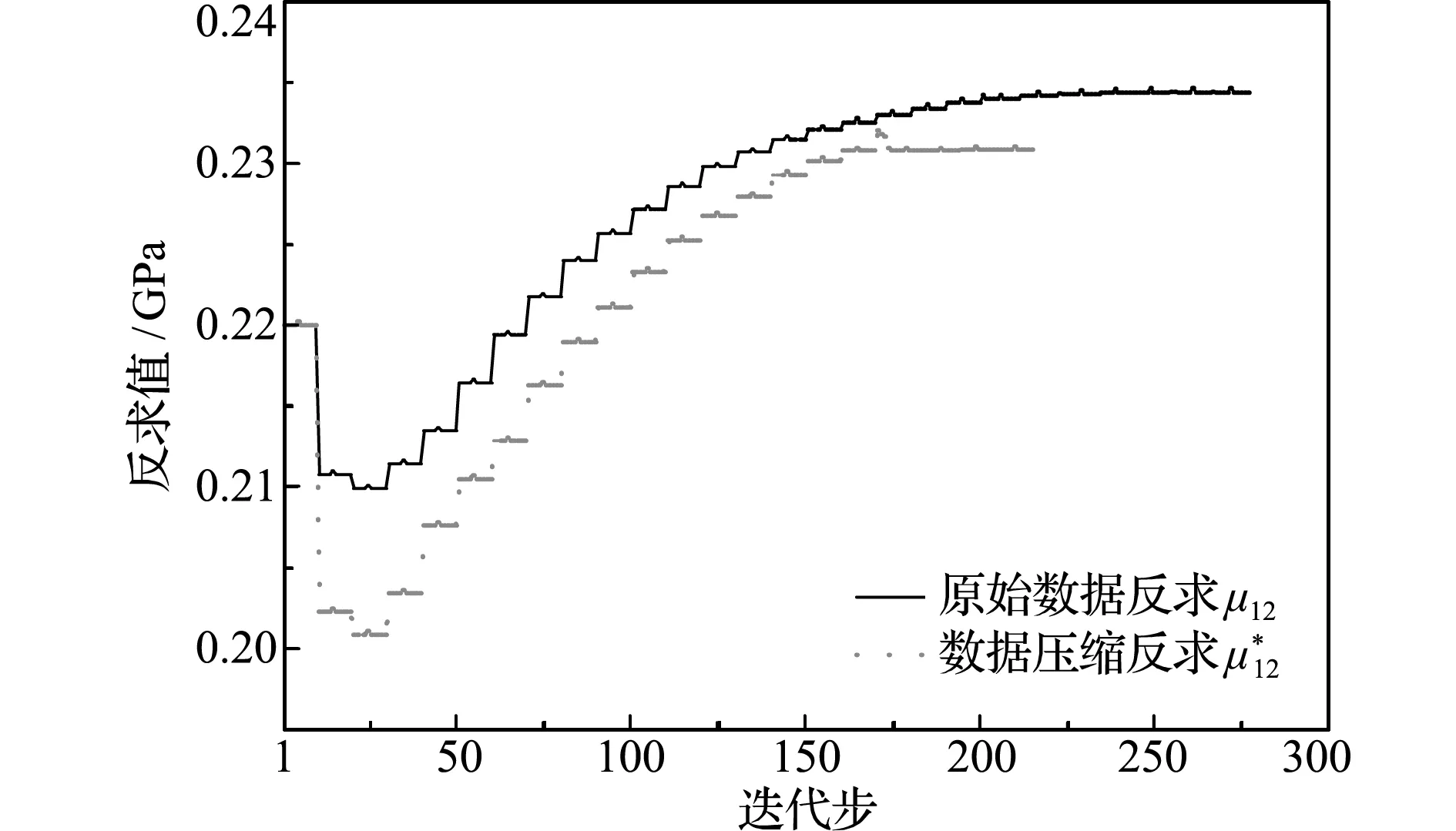
4.2 复合材料三点弯曲试验

4.3 方法的抗噪性
5 结 论
