Ce掺杂6H-SiC电子结构和光学性质的第一性原理研究

邹 江,周庭艳,熊中刚,曾丽娟,吴 波

(1.遵义师范学院物理与电子科学学院,遵义563006;2.桂林航天工业学院,桂林 541004)

1 引 言

SiC作为第三代半导体，具有宽禁带、高的热导率、抗磁性.在大功率，传感器，磁光电等领域有巨大的应用潜质[1-6].以碳化硅(SiC) 、氮化镓( GaN)、金刚石、氧化锌(ZnO)、氮化铝(AlN)为代表.

利用掺杂的方法可以改变材料的性能，关于不同材料掺杂SiC做了大量研究.周鹏力等[7]对B-Al共掺杂3C-SiC的电子结构和光学性质进行研究.彭彩云[8]等对4H-SiC材料p型掺杂的电子结构进行研究.范梦慧等对4H-SiC表面空位进行大量的研究.林龙等[9-10]研究得出通过Cr掺杂4H-SiC会产生磁矩.此外，还有许多对SiC的其它性质进行了研究[11-13]，但对Ce掺杂6H-SiC的电子结构和光学性质的理论计算尚未见报导.

因此采用基于密度泛函理论的(Density functional theory，DFT)第一性原理计算方法，计算未掺杂6H-SiC及Ce掺杂6H-SiC的电子结构和光学性质，研究Ce掺杂对6H-SiC的电子结构和光学性质的影响.

2 构建模型和计算方法

6H-SiC的空间群为P63MC，其晶格常数a=b=3.080 Å，c=15.11 Å 6H-SiC的晶胞如图1所示.计算采用2×2×1的6H-SiC超晶胞，6H-SiC超晶胞的晶格常数a=b=6.160 Å,c=15.11 Å，Ce掺杂采取的是替位式掺杂，一个Ce原子替代一个Si原子的位置，超晶胞模型，其结构模型如图1所示[14].

在Material Studio软件中的CASTEP模块进行理论计算，其计算原理是基于密度泛函理论的从头计算量子力学方法，采用广义梯度近似(GGA)的PBE方案近似处理电子与电子之间的相关关联能[15].首先采用CASTEP模块对超晶胞进行几何结构优化，得到稳定的结构体系，再分别计算未掺杂和Ce掺杂的电学性质和光学性质.

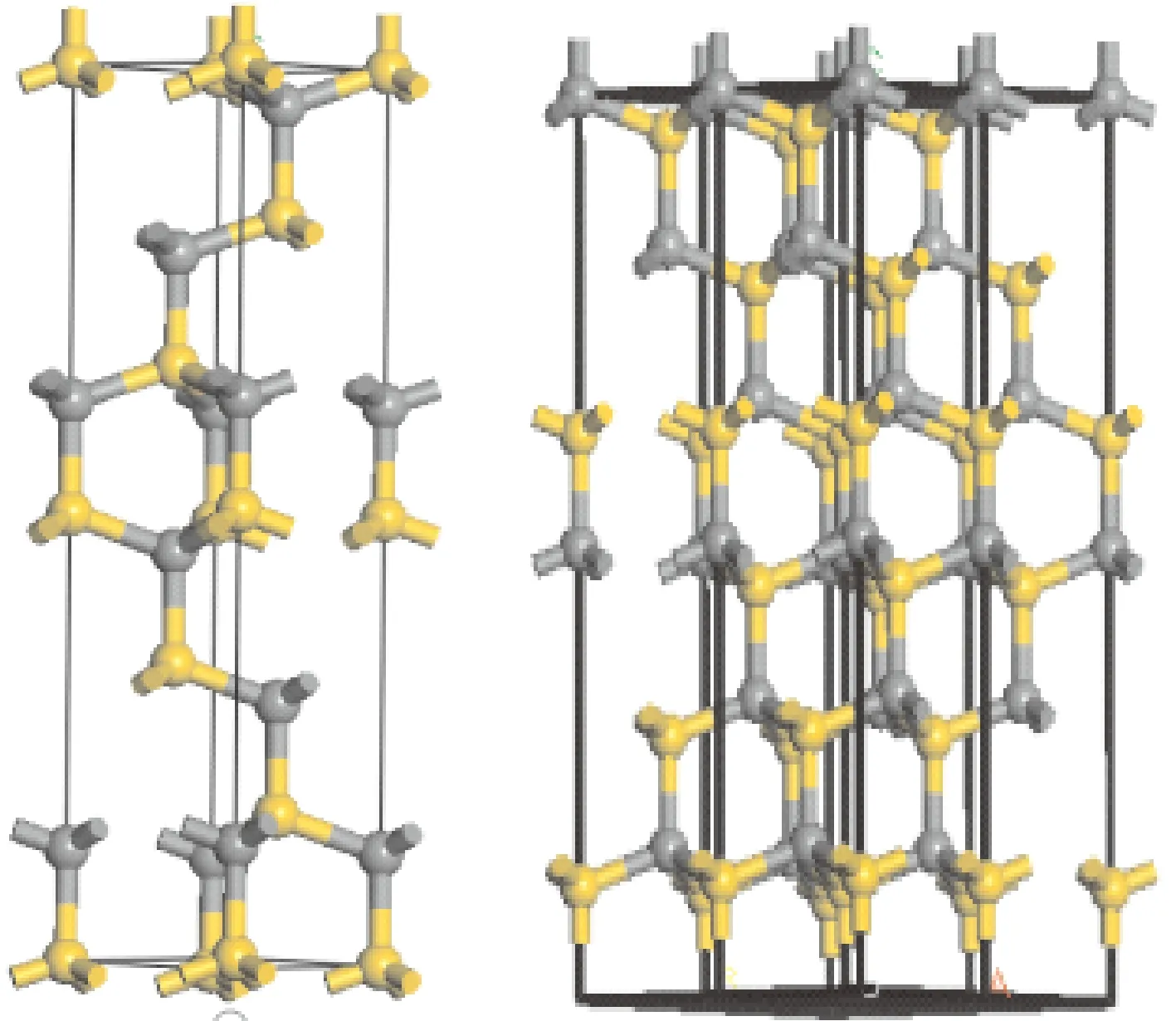
图1 6H-SiC晶胞结构和超晶胞结构Fig.1 Cell structure of 6H-SiC

3 计算结果分析

3.1 几何结构

对未掺杂6H-SiC、Ce掺杂6H-SiC前后的超晶胞模型进行几何优化，计算结果的晶胞几何参数和总能量见表1.从表中可以看出，平衡晶格常数实验误差小于1%，说明计算结果比较准确，此计算方法可以计算其他性质[16].未掺杂6H-SiC晶格体积为0.332 nm3，Ce掺杂后体系的晶格体积为0.517 nm3，说明掺杂体系的晶格体积稍有增大，根据量子化学观点，Si原子半径小于掺杂原子(Ce)的半径，所以当Ce原子替代Si原子后，在一定程度上破坏了晶格周期性，其晶格发生畸变，因此晶格体积有所增大[17].未掺杂6H-SiC、Ce掺杂体系能量分别为 -145.8231 eV、-1055.2932 eV，因此比未参杂6H-SiC稳定.

3.2 能带结构和态密度

图2(a)为未掺杂 6H-SiC的能带结构，图2(b)为Ce掺杂6H-SiC的能带结构.由图2(a)可知，未掺杂的6H-SiC，是间接半导体，导带最低点在L点，价带最高点在G点，其禁带宽度2.045 eV,比实验值略小，这是由于计算采用的GGA近似方法低估了激发态电子间的相互作用造成的.由(b)中可以得到，掺杂Ce元素，导带最低点在A点，在M点取得最大值，禁带宽度为0.812 eV.掺杂后引入了新的杂质能级.6H-SiC的Si原子的2s轨道与2p轨道发生杂化形成sp3轨道，而C原子的3s轨道与3P轨道发生杂化形成sp3轨道，两个sp3轨道发生能级分裂，形成能量较低的成健态和能量较高的反键态，成键态形成6HSiC的价带，反键态形成其导带.掺杂Ce原子后，Ce原子发生能级交错，4f轨道的能量大于5d轨道的能量，5d轨道的能量大于6s轨道的能量，Ce原子的4f 、5d轨道主要贡献在导带.4f轨道是7重简并，5d轨道是5重简并，掺杂后4f轨道、5d轨道未发生能级分裂.

为了进一步研究Ce掺杂对6H-SiC电子结构变化的影响，计算了未掺杂和及Ce掺杂6H-SiC的态密度，图3(a)和图3(b)分别为未掺杂6H-SiC和Ce掺杂SiC的态密度图和各原子的分波态密度图.由图3(a)可知未掺杂6H-SiC在能量从-15-10 eV之间，主要由Si-3s、C-2s贡献，能量从-10-0 eV之间，主要由Si-3p、C-2p电子轨道贡献，而在导带主要受Si-3p、Si-3s贡献.从图3(b)可以看出，在价带的低能区，主要由Si的Si-3s、C-2s、Ce-5p构成.在价带的高能区，主要由Si-3p、C-2p贡献.Ce原子的5p及5d轨道贡献较小，而Ce原子的4f轨道没有贡献.而导带主要由Si-3p、Ce-4f轨道贡献，而Ce原子的5d轨道贡献较小.掺杂后处于导带的有效质量比价带的有效质量小，导带的迁移率更高.说明处于导带底状态时更容易迁移.根据波尔兹曼方程，电导率与费米面的态密度成正比，所以掺杂后电导率提高，其导电性增强，其原因是由于掺杂原子的引入，能进入导带的电子数增加.

表1 几何结构优化后的Ce掺杂6H-SiC的晶格常数和总能量Table 1 Lattice constants and total energies of 6H-SiC and Ce doped 6H-SiC after the geometrical structure optimization

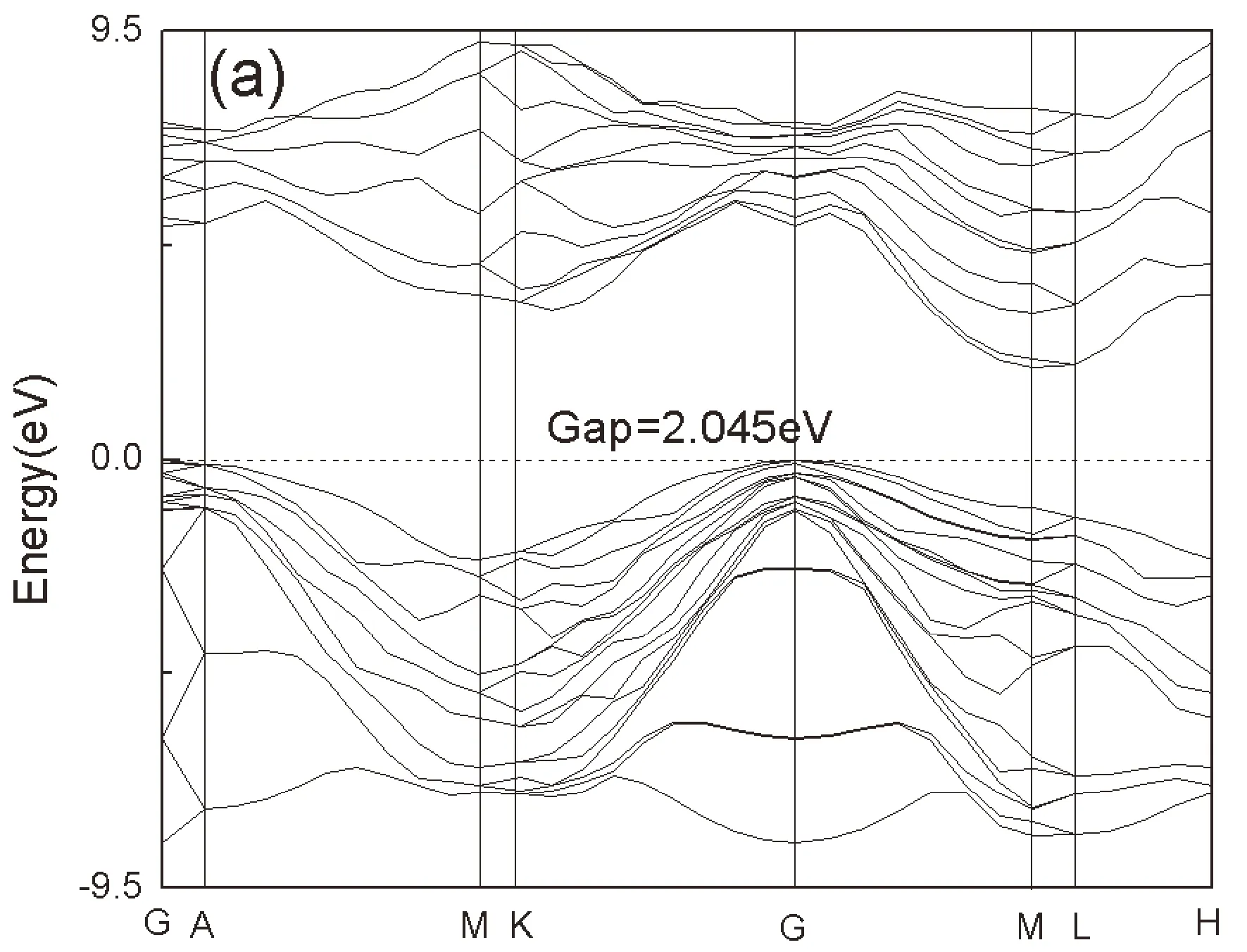
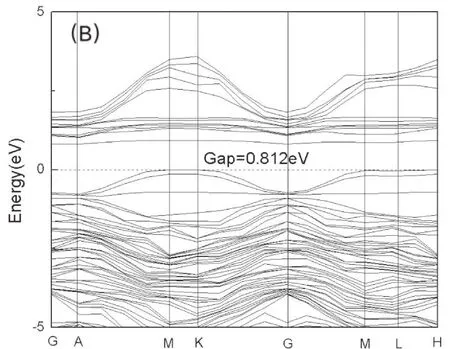
图2 (a)6H-SiC的能带结构;(b)Ce掺杂6H-SiC的能带结构.Fig.2 (a)Band structure of 6H-SiC;(b)Band structure of Ce doped 6H-SiC.

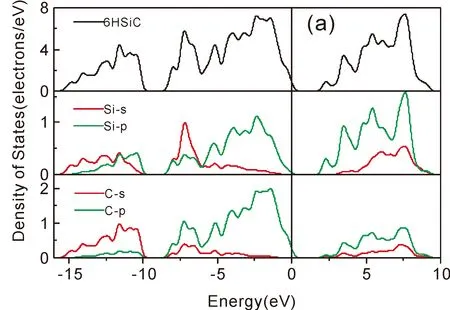
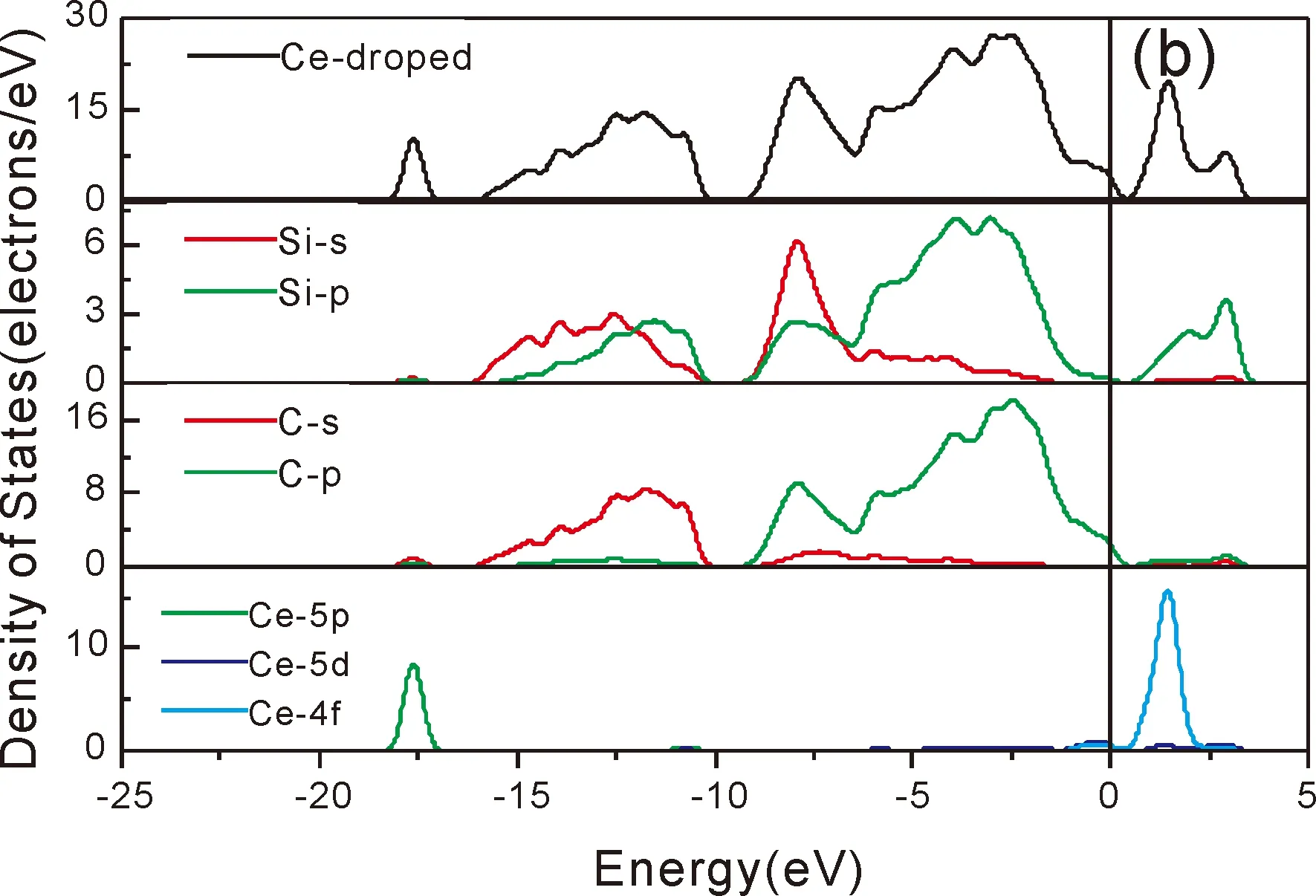
图3 (a)6H-SiC的态密度和分波态密度;(b)Ce掺杂6H-SiC的态密度和分波态密度.Fig.3 (a)Density of states and density of atomic states of 6H-SiC;(b)Density of states and atomic density of atomic states of Ce doped 6H-SiC.

3.3 光学性质

3.3.1介电函数

介电函数是沟通电子跃迁微观物理过程与固体电子结构的桥梁，其反映了固体能带结构，通过介电函数能得到其它各种光谱信息.固体宏观的光学特性函数可以通过其介电函数来表示[18]：

ε(ω)=ε1(ω)+iε2(ω)

(1)

其介电函数实部为ε1(ω)，介电函数虚部为ε2(ω)，图4(a)和图4(b)分别为未掺杂4H-SiC和B掺杂6H-SiC以及Ce掺杂6H-SIC的介电函数实部ε1(ω)和虚部ε2(ω)与入射光子能量的关系.从图4(a)中可以得到未掺杂6H-SiC的静态介电常数为6.37，Ce掺杂6H-SiC的静态介电常数为4.25.从图4(b)中可以得到未掺杂6H-SiC在能量6.64 eV，出现一个峰值16.23，这是由于价带电子跃迁到导带电子所致.Ce掺杂后，出现2个介电峰，第一个介电峰在能量1.38 eV处，第二个介电峰在能量5.43 eV处.第一个介电峰是由于导带电子跃迁到Ce原子4f轨道上产生，第二个峰是价带电子向导带电子跃迁产生.

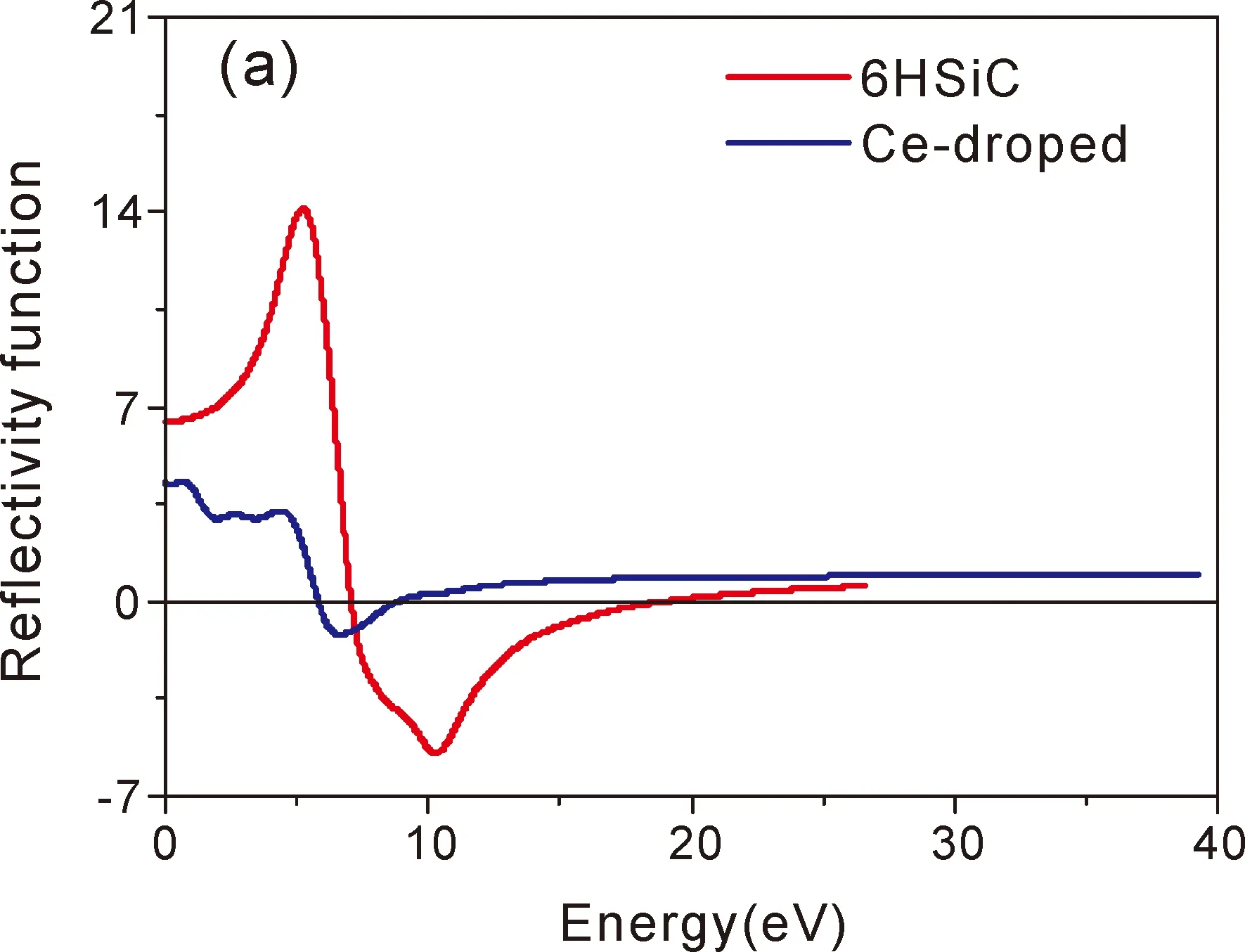
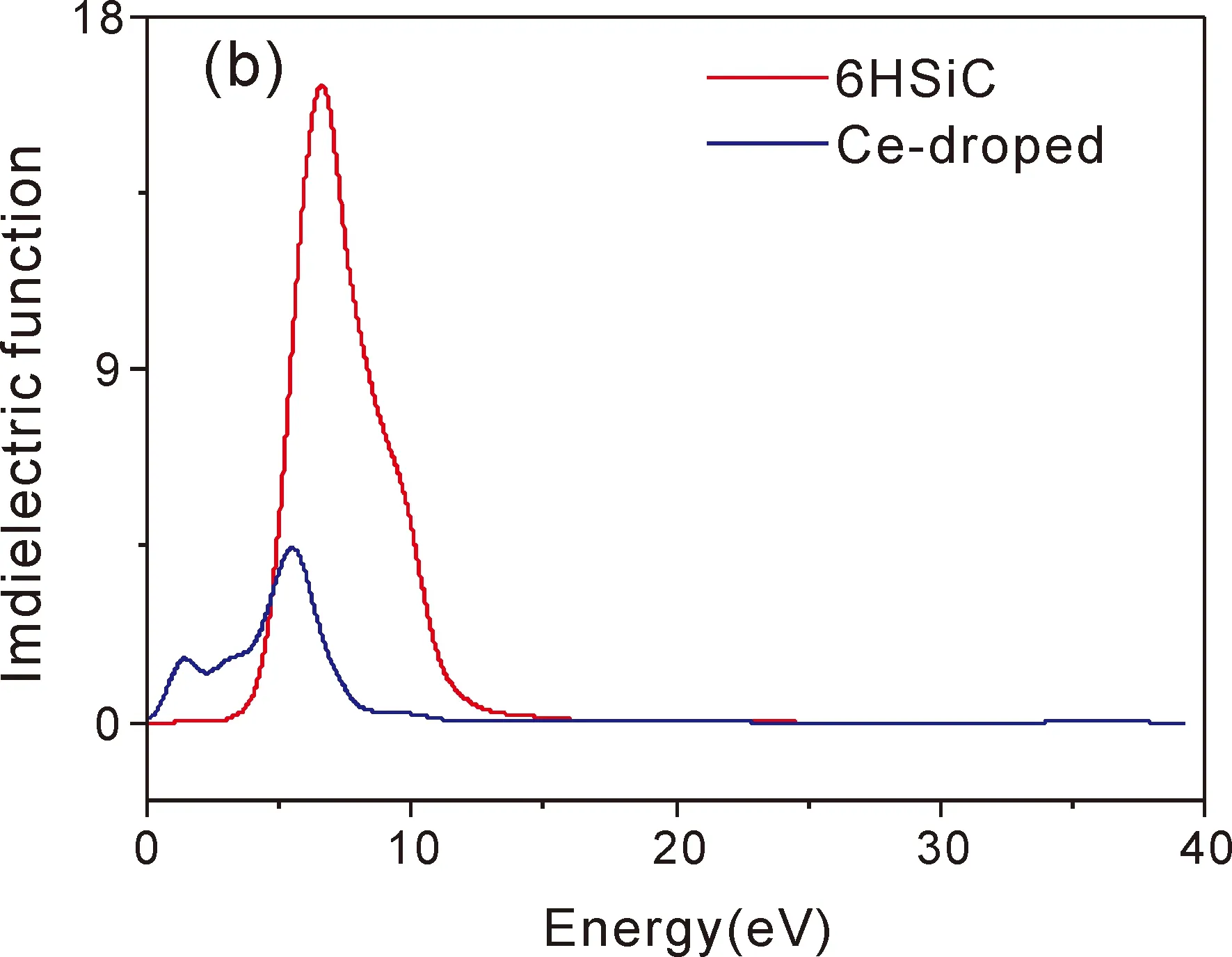
图4 复介电函数:(a)实部,(b)虚部.Fig.4 The dielectric functions:(a)real parts,(b)imaginary parts.

3.3.2吸收谱和反射谱

半导体吸收系数指的是光波在此半导体介质中单位传播距离光强度衰减百分比.图5(a)和图5(b)及分别为未掺杂6H-SiC和La掺杂6H-SiC的吸收谱和反射谱.由图5(a)可知，6H-SiC在3.6 eV-19 eV都有吸收系数，而在能量为10.31处吸收系数达到最大值.而Ce掺杂6H-SiC以后，吸收系数发生了较大的变化，从0 eV开始就有吸收系数，在能量大于12 eV后，吸收系数为0.能量在0 eV-12 eV中，有一个吸收峰，位于6.37 eV处.掺杂后的6H-SiC，其吸收系数降低.由(b)图可知，反射率变化比较大，未掺杂6H-SiC在能量为16.59 eV处取得最大值，而Ce掺杂后在能量为7.99 eV处取得最大值.

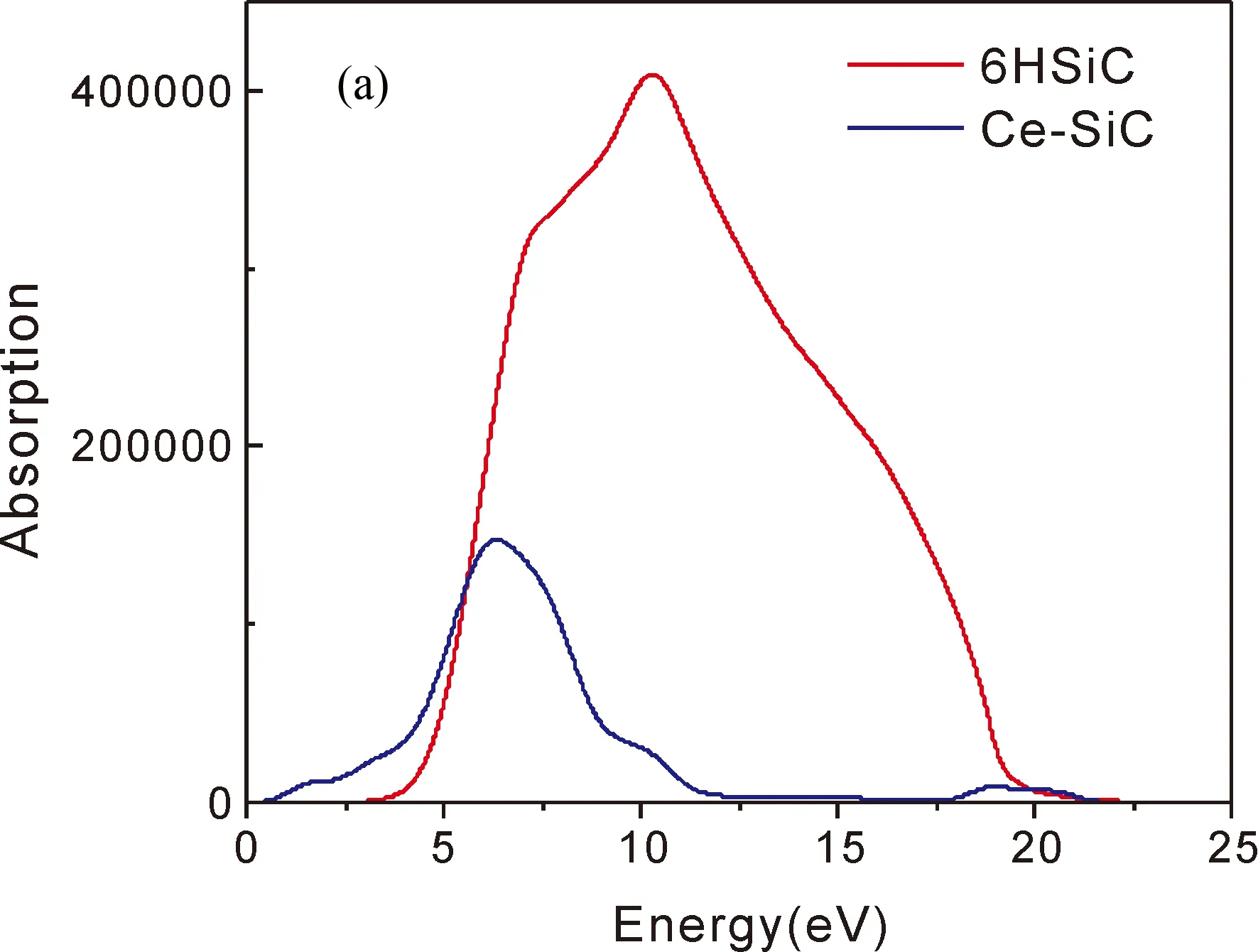
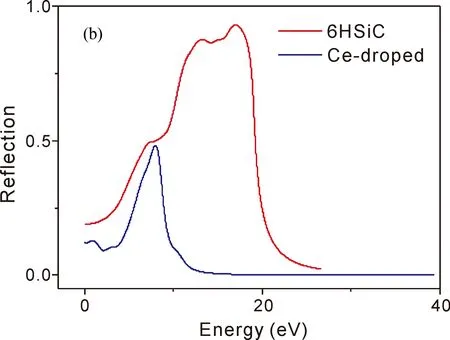
图5 (a)吸收谱;(b)反射谱.Fig.5 (a) Absorption spectrum;(b) Reflection spectrum.

4 结 论

采用第一性原理计算方法，先后计算未掺杂6H-SiC和Ce掺杂6H-SiC的电子结构和光学性质.计算结果表明，未掺杂的6H-SiC，是间接半导体，其禁带宽度2.045 eV.掺杂Ce元素，禁带宽度为0.812 eV，掺杂后引入了新的杂质能级.6H-SiC的两个sp3轨道发生能级分裂，形成能量较低的成健态和能量较高的反键态，成键态形成6HSiC的价带，反键态形成其导带.掺杂后处于导带的有效质量比价带的有效质量小，导带的迁移率更高.说明处于导带底状态时更容易迁移.根据波尔兹曼方程，电导率与费米面的态密度成正比，所以掺杂后电导率提高，其导电性增强，其原因是由于掺杂原子的引入，能进入导带的电子数增加.Ce掺杂后，出现2个介电峰，第一个介电峰在能量1.38 eV处，第二个介电峰在能量5.43 eV处.反射率变化比较大，未掺杂6H-SiC在能量为16.59 eV处取得最大值，而Ce掺杂后在能量为7.99 eV处取得最大值.