“宏观辨识与微观探析”素养在课堂教学中的落实—以晶胞中原子坐标参数为例

，

(新疆师范大学附属中学，新疆 乌鲁木齐 830054)

学科核心素养是学科育人价值的集中体现，是学生通过学科学习而逐步形成的正确价值理念、必备品格和关键能力。“宏观辨识与微观探析”核心素养很好地体现了化学的学科特征[1]。

《课程标准·2017版》在选择性必修模块的“内容要求”中指出“了解晶体中微粒的空间排布存在周期性，认识简单的晶胞”。能自发形成的规则的几何外形是区别晶体和非晶体的重要标志。晶体内部微观粒子周期性的有序排列是宏观呈现规则几何外形的根本依据。化学上引入的“晶胞”这个概念作为研究晶体宏观和微观的桥梁。“晶胞”是课堂教学中落实“宏观辨识与微观探析”核心素养有效载体[2]。

原子坐标参数是晶胞的基本要素，用来表示晶胞内部各原子的相对位置。此部分知识在现行的高中教材中没有系统地介绍，现整理介绍如下：

1 构建坐标原点、坐标轴和单位长度

我们从最简单的晶胞--简单立方堆积的晶胞模型入手，构建坐标原点、坐标轴和单位长度。

简单立方堆积的晶胞中8个顶点的微粒是完全一致的，因此可以任意选择一个原子为坐标原点。以立方体的三个棱延长线构建坐标轴，以晶胞边长为1个单位长度。由此可得图1所示的坐标系。

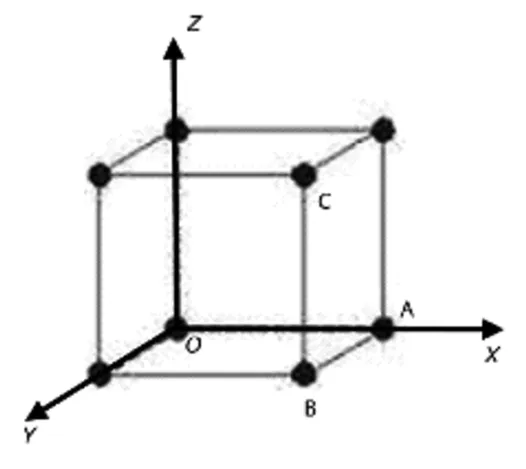
图1 晶胞坐标系

其它晶胞也可以采用这种方式构建。六方最密堆积模型的晶胞按此法构建x轴和y轴夹角不是90°，而是120°。但这并不影响后续问题的讨论。

2 原子坐标参数的两个特性

2.1 原子坐标取值范围是[0,1)

我们建立了如图1的坐标原点和坐标轴。O点的坐标可以确定为(0,0,0)。我们以晶胞边长为1个单位，可以直接得出 A、B、C点的坐标分别是(1,0,0)、(1,1,0)、(1,1,1)。但这样是不合适的。晶胞是无隙并置构成晶体的，也就是说晶胞具有平移的特性。如果我们把这个晶胞沿着x轴方向平移一个单位，O点就到了A点，它们是相同的原子，实际上处于相同的位置。同理A点沿着y轴方向、z轴方向平移可以到达B、C点。

基于此，对原子坐标做出如下规定：以晶胞边长为1个单位，坐标取值范围是[0,1) 。图中A、B、C点的坐标都是(0,0,0)。

2.2 晶胞中分数坐标的数目和微粒计数相同

图2(a)(b)分别是体心立方和面心立方的晶胞模型。

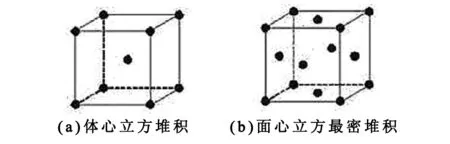
图2 晶胞模型

我们列出图2所有原子的坐标参数如表1所示。

表1 体心立方和面心立方的晶胞中所有原子的坐标参数

从表1中可以得出这样的结论：晶胞中分数坐标的数目=微粒计数。

3 原子坐标参数的应用

3.1 常见原子坐标参数

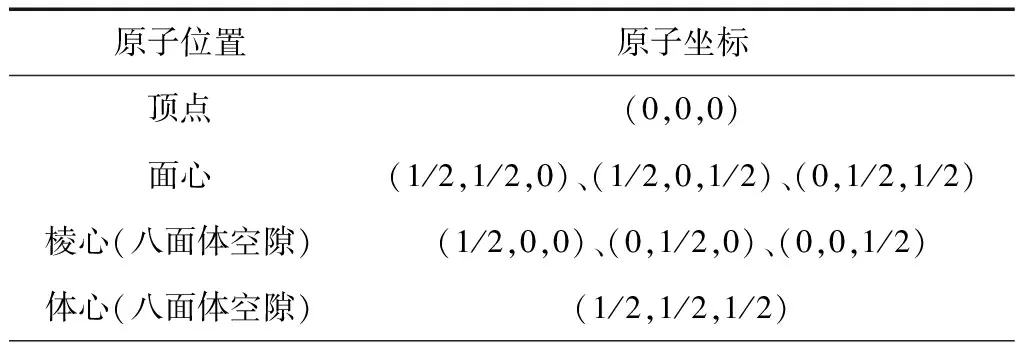
表2 立方晶胞中5种常见的原子坐标参数

表2(续)

(1)高中阶段研究最多的晶胞是立方晶胞，即晶胞参数a=b=c，α=β=γ=90°的晶胞。此类晶胞有5种常见的原子坐标参数，具体如表2所示。

(2)2016年全国Ⅰ卷第37题(6)问如下：

晶胞有两个基本要素：①原子坐标参数，表示晶胞内部各原子的相对位置，图3为Ge单晶的晶胞，其中原子坐标参数A为(0,0,0)；B为(1/2,0,1/2)；C为(1/2,1/2,0)。则D原子的坐标参数为______。

图3 Ge单晶的晶胞

通过分析，这道高考题构建了和我们前文中类似的坐标系。D点所处的位置是四面体空隙，即体对角线的1/4，因此可以得出它的坐标参数为(1/4,1/4,1/4)。

3.2 坐标平移

(1)晶胞是一个人为规定的概念，对于同一个晶体结构，有时候有多种合理的方式选取晶胞。不同种方式选取的晶胞，各微粒的原子坐标参数虽会发生变化，但微粒的相对位置并没有改变，可以通过坐标平移的手段来快速判断。所谓的坐标平移就是在现有晶胞的原子坐标参数基础上加上或者减去一组坐标值。

(2)2017年全国Ⅰ卷第35题(5)问如下：

KIO3晶体是一种性能良好的非线性光学材料，具有钙钛矿型的立方结构，边长为a=0.446 nm，晶胞中K、I、O分别处于顶角、体心、面心位置，如图4所示。在KIO3晶胞结构的另一种表示中，I处于各顶角位置，则K处于______位置，O处于______位置。

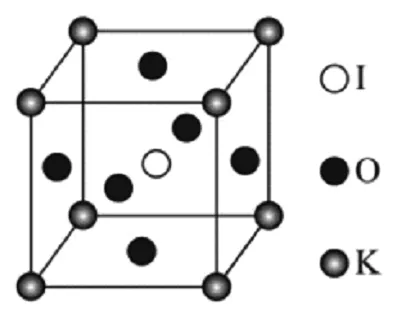
图4 KIO3晶体晶胞

K处于体心的位置是容易得出的结论。这个结论的得出可以从K与I交换了位置得到，也可以从K和I都在晶胞中的微粒计数为1可以得到。O的位置确定较为困难，因为当O在面心和棱心位置上微粒计数都是3。采用原子坐标参数，并对其进行平移，可以使得问题简单化。思路如表3所示。

表3 利用坐标平移分析KIO3晶体中微粒所处的位置

3.3 微粒间距离

(1)晶胞微粒间距离的计算是一类常见题目。一般通过几何方法去做。目前，高中数学中淡化了欧式法解决立体几何的问题，建系是常见解决立体几何问题的思路。基于此，学生在求解晶胞中微粒间距离时因空间想象能力弱而丢分严重。应用原子坐标参数可以很快解决晶胞微粒间距离的问题。

令立方晶胞的晶胞参数为a pm，A和B两微粒的原子坐标参数分别为(x1,y1,z1)(x2,y2,z2)。

AB两微粒间距离可直接写出dA-B=[( x1- x2)2+(y1- y2)2+( z1- z2)2]1/2a pm。

(2)如图5a是立方硫化锌晶胞，已知晶胞参数a=541pm，计算AB两点间距离。

图5 立方硫化锌晶胞及其坐标系

在题目情景中AB两点的几何关系较难确定，用构建三角形的方法解决不容易。用原子坐标参数可以快速求解。建立如图5b所示的坐标系，写出A、B两点的坐标分别是(0,1/2,1/2)、(3/4,3/4,1/4)。其距离为：

dA-B=[(0- 3/4)2+(1/2- 3/4)2+( 1/2- 1/4)2]1/2× 541pm=448.6pm。

构建原子坐标参数可以帮助学生从“微粒位置-晶胞-晶体”三个层次对晶体结构进行认识。它可以把复杂的晶胞结构图数字化，具体化，方便我们掌握原子之间的位置关系，也可以通过平移关系帮助我们更好理解晶体规则几何外形的形成。这个过程有助于培养学生的“宏观辨识与微观探析”核心素养。