炮射弹药滑动导带环结构设计
2021-07-30潘明然高志斌郭明珠倪庆杰
刘 猛,潘明然,高志斌,郭明珠,杨 莹,倪庆杰
(1 沈阳工学院,沈阳 110000;2 辽沈工业集团有限公司,沈阳 110045)
0 引言
随着精确打击弹药在战争中的地位不断提高,美俄等军事强国以中大口径身管火炮为平台,大力发展可兼容射击的制导弹药[1],由于较高的离心过载对制导炮弹采用的敏感测量器件、电控器件影响较大,对制导控制影响也较大,因此目前的制导炮弹均采用滑动导带减旋技术,减小弹丸的出炮口转速,采用尾翼稳定装置来保证弹丸飞行稳定。制导炮弹滑动导带减旋技术是常规弹药制导化的关键技术之一,其稳定工作是武器系统制导、控制部件正常作用的前提。滑动导带环由滑动导带体和镶嵌在导带体上的导带组成。发射时,嵌入膛线的滑动导带环做高速旋转,弹体在与滑动导带环接触面的摩擦力矩作用下微旋,滑动导带环同时闭住高压火药气体,避免对火炮身管内膛和弹丸导带前部的冲刷。
滑动导带环工作环境及工作过程相对制式弹药的导带复杂很多,且目前国内尚无成熟、完善的工作过程理论分析及计算方法。文中对线膛火炮发射弹药的三圆孔式滑动导带环结构形式、作用原理进行分析研究和试验验证,提出了滑动导带环设计需要关注的几个问题。
1 三圆孔式导带环的结构形式及作用原理
1.1 结构形式
三圆孔式导带环结构如图1所示。三圆孔式导带环由滑动导带体和铜质导带组成,滑动导带体内径由3个直径不同的圆柱体组成[2]。滑动导带体选用高强度合金钢,环上镶嵌铜质导带。根据减旋需要,滑动导带环前端面可涂不同的润滑涂层,以减小滑动导带环与弹体之间的摩擦力,达到降低弹丸转速的目的。
三圆孔式导带环主要有两个作用:其一为闭气,同时在滑动导带环内径与弹体间形成气室,减小滑动导带环与弹体的相互碰撞;其二为减旋,需要圆环内径与弹体留有一定的间隙,以达到减旋效果;同时要控制好图1中的B,C面以及G,D面的尺寸间隙,保证可靠闭气。

图1 三圆孔式弹带环结构图
1.2 工作原理
内圆柱设计成三段式是保证滑动导带环与弹体间进入火药气体。弹丸入膛时,滑动导带环的H面嵌入膛线,此时火药还没作用,滑动导带环向后移动,C面接触。发射药开始作用,随着压力逐渐增大,推动弹丸向前运动,此时导带已经进入膛线,导带的轴向剪切力逐渐减小,作用在滑动导带环上的力主要有火药气体的推力、滑动导带环的直线后座力以及导带与火炮膛线的摩擦力,从设计上要保证火药气体的推力大于滑动导带环的直线后座力以及导带与膛线的摩擦力,滑动导带向前运动,A面接触,通过摩擦力矩带动弹体旋转。这样就避免滑动导带环在膛内挤进及运动过程中与弹体接触,从而对弹体产生撞击,减小弹丸的飞行抖动。
2 仿真分析
2.1 滑动导带环强度分析
导带挤进膛线时,滑动导带体受力最大,此时要保证滑动导带体的强度满足要求,铜质导带的强度要满足导转的要求。
2.1.1 计算导带挤入膛线的压力
铜质导带的挤进压力是校核导带环强度的基础。导带挤进压力有试验测定和工程计算两种方法[3]。滑动导带环的导带挤进压力计算没有成熟方法,文中以某产品为例,利用文献[2]给出的常规炮弹导带压力计算公式,计算滑动导带环的导带挤入膛线[4]的压力。
滑动导带所受局部载荷Pb1与滑动导带变形ω0的关系式为:
Pb1=A0+B0ω0
(1)
式中:A0,B0是与滑动导带材料有关的系数,分别为:
(2)
(3)
其中系数0.94是对目前各种榴弹适用的系数;K值为由壳体理论推导出来的变形与载荷关系的系数,在导带不是弹底位置情况下:
(4)
式中β由弹性理论得出:
(5)
其次求出导带压力的传递关系。由导带的大变形规律可以导出:
Pb-Pb1=A1+B1ω0
(6)
式中A1,B1是与导带材料有关的系数。
(7)
(8)
最后再求滑动导带压力与导带变形的关系。假设导带充满火炮膛线,可得:
Pb=A2-B2ω0
(9)
其中A2,B2也是与导带尺寸、材料有关的系数。
(10)
(11)
综合上述公式,求得:
(12)
式(1)~式(12)中的符号分别表示:r0为导带区滑动导带环中间半径;h0为滑动导带环导带区壁厚;E0为滑动导带环弹性模量;λ0为滑动导带环的强化参数;δs0为滑动导带环的屈服强度;ω0为滑动导带环压缩变形,半径上的位移量;ra1为导带内半径;rb1为导带外半径;h1为导带厚度;b为导带宽度;E1为导带弹性模量;λ1为导带的强化参数;σs1为导带的屈服强度。
根据以上计算公式,代入相关数据,计算某弹滑动导带环的挤进压力为Pb=289 MPa。
2.1.2 滑动导带体强度仿真分析
已知导带的挤进压力,利用ANSYS软件对滑动导带体进行结构强度仿真分析。计算模型如图2所示。
图2 滑动导带体仿真模型
假设条件:滑动导带体前端面压在弹体上;某产品的导带挤进压力为289 MPa,火药气体压力取起动时的压力40 MPa。
经过仿真分析,滑动导带体最大变形量为0.18 mm,最大等效应力为980 MPa,因此要求滑动导带体的屈服强度大于980 MPa,结果如图3、图4所示。
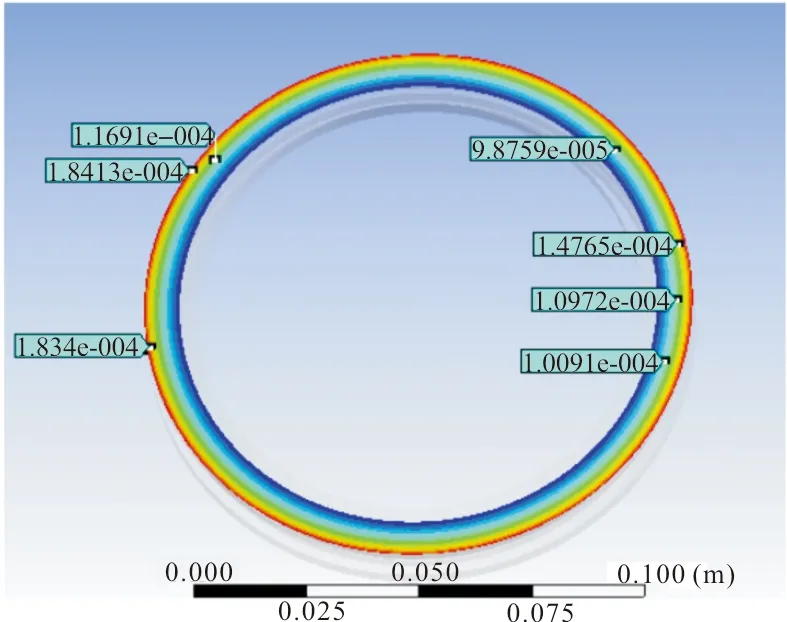
图3 滑动导带体形变图

图4 滑动导带体前端面应力图(前端面与弹体接触)
2.1.3 铜质导带的强度校核
作用在导带上的压力为:
(13)
式中:N为导转侧力;Bts为导带受力面积。
对于等齐膛线
(14)
经换算得:
(15)
导带的抗压强度条件为:
σ≤[σ]
(16)
式中:[σ]为导带的抗压强度许可值。
导带凸起部受到的剪切应力为:
(17)
对于等齐膛线
(18)
导带的剪切强度条件为:
τ≤[τ]
(19)
式中[τ]为导带的抗压强度许可值。
代入某弹的数据,铜质导带的膛内强度校核计算结果如表1所示。由计算结果可知,导带满足挤进及剪切强度要求。

表1 导带膛内强度校核计算结果 单位:MPa
2.2 滑动导带环与弹体的接触力分析
为了实现滑动导带的减旋效果,要保证滑动导带环在膛内运动时,前端与弹体接触。这样在结构尺寸设计时,需保证火药气体对滑动导带环的推力大于滑动导带环的直线后座力和摩擦力之和。
滑动导带环与弹体之间的相互作用力Q的计算公式为[1]:
(20)
F=f·N
(21)
式中:rcp为考虑火炮膛线时,炮膛断面的换算半径;P为膛压;ra为滑动导带环内表面半径;m为弹丸质量;mb为滑动导带质量;F为导带对火炮膛壁的摩擦力(即由导带侧压和导带压力所产生的总摩擦力);f为摩擦系数,本产品为钢与铜的摩擦系数,取0.21;N为导转侧力,公式为:
(22)
式中:Jx为弹丸的极转动惯量;n为膛线条数;α为火炮缠角。
以某产品的滑动导带环为例,代入相关数据,计算出相互作用力为Q=924 658 N。
2.3 弹丸转速估算
采用弹丸转速计算公式,计算由摩擦力矩产生的弹丸转速。
根据滑动导带环与弹体之间的作用力Q引起的摩擦力矩M为:
(23)
式中:rh为弹底压螺外半径;f1为滑动导带环与弹体间的摩擦力。钢与钢之间的摩擦系数为0.15,根据需要,可以增加润滑涂层,摩擦系数可以达到0.05以下。

(24)
为了便于积分,近似取平均膛压Pcp及平均摩擦力Fcp代替公式中的P和F,从而有:
(25)
式中,tg为弹丸沿炮膛运动的时间。
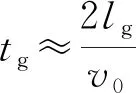
(26)
式中,lg为弹丸沿炮膛运动的全行程。

(27)
以某弹的滑动导带环为例,计算弹丸的最小炮口转速[5]为:
ωmin=7.1 r/s
由计算结果可知,如果滑动导带环设计理想,理论上该弹的炮口最小转速可以达到7 r/s左右。但由于有其它因素的影响,尤其代入计算的Fcp与真实的数据有出入,滑动导带环与弹体接触面的光洁程度也有差别,目前测得实际的转速要比计算的略高。
3 试验验证
某产品的滑动导带环设计成三圆孔式结构。在初速为500 m/s时,理论计算的最小炮口转速为7 r/s,实测转速为15.4 r/s,满足制导控制要求。检查回收的滑动导带环,前端面有与弹体的摩擦痕迹,滑动导带环内及前端面无火药气体冲刷痕迹,说明闭气效果良好,如图5所示。

图5 试验用滑动导带环结构示意图
4 结论
给出了该产品滑动导带体强度与铜制导带强度的计算方法,并且介绍了转速的理论计算方法,通过计算与仿真,得出该滑动导带环的结构强度满足设计要求,减旋与闭气效果满足设计要求,同时进行了试验,试验发现:1)滑动导带环满足挤进膛线时的强度要求以及膛内运动的正确性要求。2)保证三圆孔结构的配合间隙尺寸,使滑动导带环与弹体之间有气室存在,避免滑动导带与弹体磕碰,减小弹丸的飞行抖动。3)通过调整起始接触面和表面涂覆种类进行交叉组合对比验证得出,滑动导带前端面起主要转速影响作用。4)滑动导带闭气效果与各部分的尺寸间隙设计有关,验证了前期理论计算与仿真的正确性。
