碳纳米管封装Si纳米团簇融化的结构演变

2020-05-15冯鹏程马家君

原子与分子物理学报 2020年2期

冯鹏程,马家君

(贵州大学大数据与信息工程学院，贵阳 550000)

1 引言

近年来，富勒烯和碳纳米管(CNT)相继被发现，其基于纳米尺寸的优美结构以及其展现出的独特性质吸引了人们广泛的关注.自CNT发现以来，由于其独特且完美的中空结构，很早就有人设想往它的内部填充其他物质[1].Pederson[2]最早从理论上证明了这种设想的可行性.此后，Iijima[3]等人率先合成了填充铅的多壁纳米管，掀起了对这种填充材料的制备及应用研究的热潮.现已有在纳米管中填充金属[4-6]、水分子[7]、有机物[8,9]、碳[10,11]、半导体材料[12,13]等的研究报告.实验上采用化学气相沉积(CVD)的方法在CNT中制备金属及金属合金纳米线，以达到防止纳米线被氧化和控制纳米线直径的目的.1999 年，Marsen和Sattler[14]采用磁控溅射的方法在石墨基底上生长出了富勒烯笼状结构的 SiNW.2006 年，Nishio 等[15]用分子动力学的方法[16]在其硕士论文中展示了采用 COMPASS 势模拟得到的具有螺旋结构的硅纳米线.上述各位研究者对CNT包裹Si纳米线和各种金属纳米线研究比较多.2008 年，Nishio 等[13]采用分子动力学模拟方法在CNT中得到了富勒烯笼状结构的 SiNW，并且使用第一性原理计算了其电子结构.2012 年，山东大学的李青青[16]模拟得到了Si16结构，但是对其他一些可能存在的Si纳米团簇结构描述的仍比较少.赵冠湘[18]等人曾报道过有关于碳纳米管表面硅纳米颗粒热稳定性的研究，但当前研究中对Si纳米团簇在CNT中的结构演变及热稳定性的研究仍甚少涉及.本文用计算机模拟20个Si四面体组成的二十面体团簇结构填充到单臂扶手型碳纳米管(SWCNT)中，下文中均采用Si-20表示这种异构十二面体团簇.采用经典分子动力学的方法模拟对其加热的过程，通过Ovito可视化的能量分析的方法研究了此复合结构中Si-20和CNT的热稳定性.

2 模拟方案

扶手型的单臂碳纳米管(SWCNT)的手性矢量为(16，16)，在SWCNT中填充Si-20纳米团簇，每个单独团簇为100个原子，一共700个Si原子，SWCNT都采用51个周期，长度为12.5436 nm，管的直径大小为2.1696 nm的分析模型.Si-20纳米团簇采用直径1.315 nm的分析模型.

模拟方法：使用经典分子动力学模拟软件LAMMPS进行运算，在三个方向上采用周期性边界条件，选用Tersoff势函数，时间步长为0.5 fs，先采用NPT系综在300 K等温驰豫500 ps,再采用NVT系综从300 K升温到10300 K，升温时间100 ns.

3 模拟结果与讨论

3.1 能量分析

通过观测总的能量变化曲线和Si和C单独的能量变化曲线，并结合可视化软件分析得出：在300 K-4050 K左右温度范围内，存在Si-20分子团簇结构的融化过程(图1).总原子数有3964个，而Si原子只有700个，因此其平均能量在总体上表现的并不是特别的明显，这点可以从Si在300 K-4050 K温度范围内的能量变化曲线非线性，而C的能量曲线是近似线性的可以看出来(图2a，2b).未经填充Si-20的SWCNT(16,16)的拐点温度为6000 K[17],在本实验中，由于Si团簇的一部分影响，SWCNT开始提前融化，拐点温度大约在4050 K左右(图1).可见Si纳米团簇的填充会使得SWCNT的熔点降低.该复合结构的融化是个循序渐进的过程，在温度上升到5200 K的时候，SWCNT完全融化完(图1).在4050 K-5100 K范围内，由于能量的影响，Si原子开始撞击SWCNT的管壁，SWCNT开始融化，由于在该温度范围之内存在着Si团簇中Si原子对SWCNT管壁的接触与撞击，因此大大降低了Si原子的平均能量，所以此时的Si原子的平均能量曲线在4050 K-5100 K范围内呈下降趋势(图2a).随着温度的继续上升，在5100 K-7240 K温度温度范围内时，这个时候Si原子和C原子完全融合在一起，彻底破坏了SWCNT的结构，因此总体平均能量开始随温度非线性上升，在温度大约为7240 K之后，达到Si和C的沸点，能量又开始呈线性变化(图1).

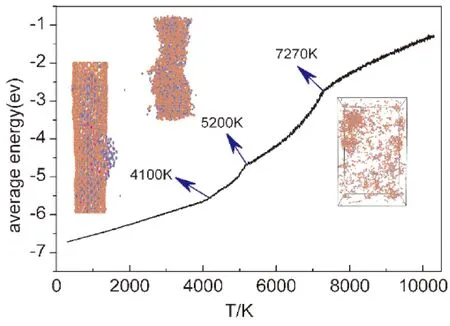
图1 不同温度下C和Si复合结构的平均势能变化图 Fig.1 The average energy of complex-structure of C and Si with different temperatures

(a)

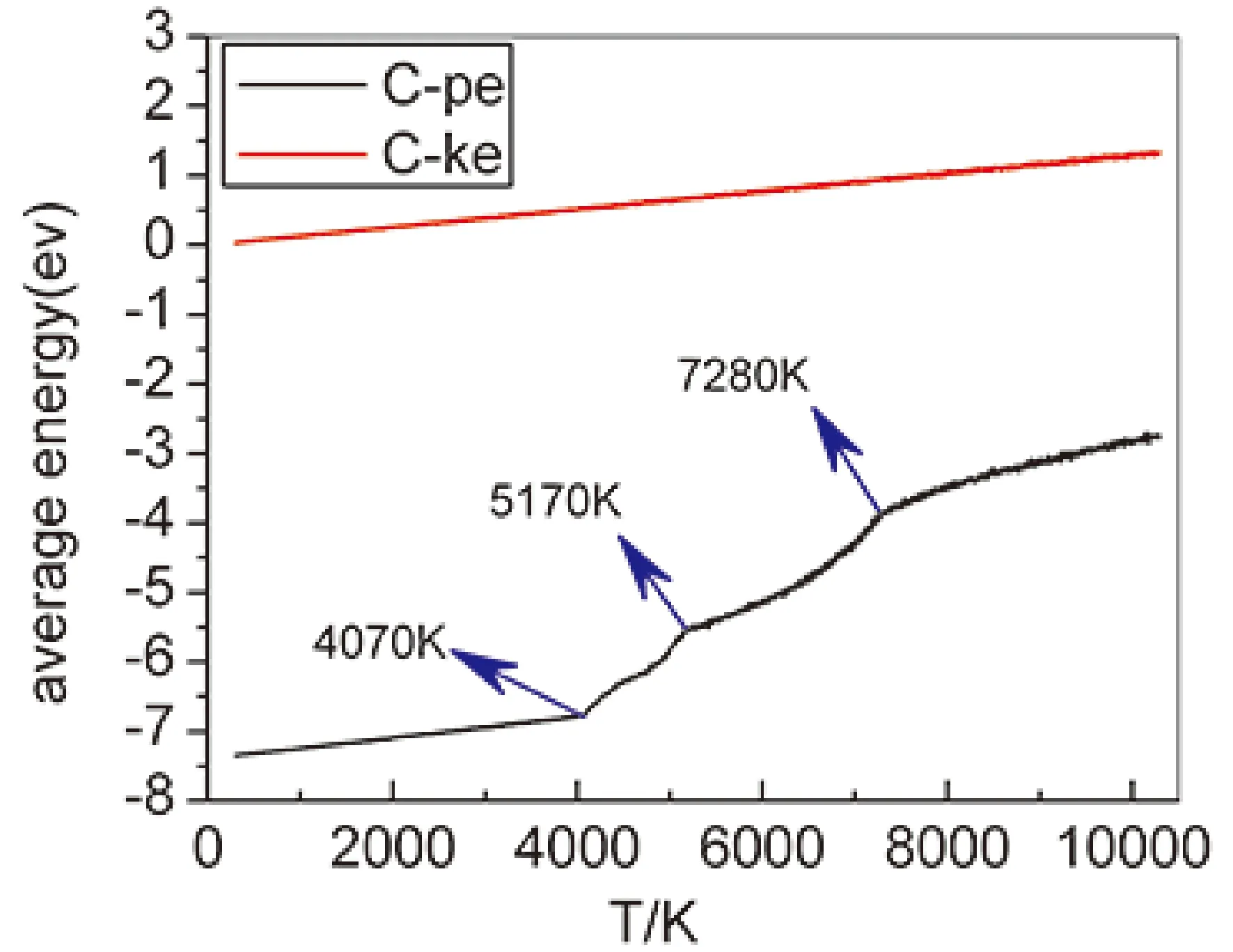
(b)图2 不同温度下C和Si平均动能和势能变化图 Fig.2 Average kinetic energy and potiential energy of C and Si with different temperatures

3.2 径向分布函数分析

3.2.1SWCNT的g(r)分布函数

在图中选取了在2200 K,3450 K,4150 K,4350 K,5200 K,7300 K不同温度下g(r)变化曲线.根据可视化软件显示出的结构变化，选取以上温度点做定性分析，通过这些温度点的选取所画出的g(r)曲线关系，从理论上来反过来验证结构变化是否符合分析结果.原始C-C键长是1.42 nm，在2200 K时，SWCNT第一峰右移，第三峰比较明显地存在，整体结构还是非常稳定.这是因为温度升高，C原子能量变大，C-C之间键长略微增大0.06 nm，但依旧处在相互平衡的状态.但是当温度在3450 K-5200 K范围内逐步升高时，第三峰开始慢慢趋于平稳，表明Si团簇在该温度范围内开始融化并最终完全融合.在图3中，温度逐步升高，SWCNT的g(r)曲线也开始有点轻微变形，这是因为存在Si团簇与SWCNT中C原子之间的范德华力的相互作用，Si团簇在SWCNT内进行周期性的上下移动.到了5200 K时第二峰也开始消失，表明这时候SWCNT开始融化，结构变化明显.到了7300 K时，第二峰完全消失，第一峰变得比较平滑，说明此时SWCNT已经几乎完全融化.

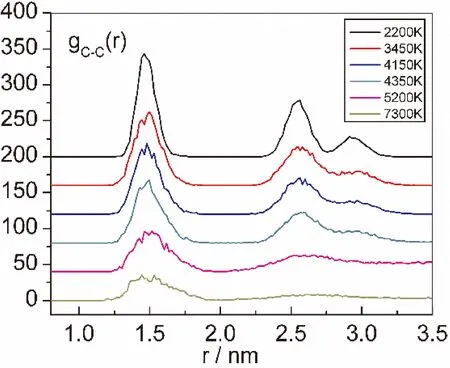
图3 SWCNT升温过程中g(r)曲线随温度的变化关系Fig.3 Relationship between g(r) and temperature in SWCNT heating process

3.2.2Si-20团簇在SWCNT中的g(r)分布函数

Si-20团簇在SWCNT中的g(r)分布函数分析，是通过在可视化软件上根据Si纳米团簇的结构变化选取温度点，画出驰豫后300 K，1500 K,1800 K,1900 K,2000 K,3000 K,4000 K不同温度下Si纳米团簇的g(r)变化曲线得到的.从而根据Si-20的g(r)变化曲线更近一步验证这种包覆结构变化的具体信息.Si-Si的键长为2.24 nm,在300 K驰豫500 ps后，由于Si原子获得能量，第一峰右移0.12 nm,且第二峰能明显观测；在1500 K时，第二峰开始趋于平滑，第三峰完全消失，此时Si纳米团簇开始接触；在1800 K时，第二峰更加平稳，第一峰波谷开始降低，Si团簇最外层金刚石结构开始融化；在1900 K时，第二峰保持，但是第一峰波谷继续变低，Si纳米团簇内层的正十二面体开始融化；在2000 K时，第一波谷再次变低,球状Si纳米团簇完全开始融合；在3000 K时，第二峰完全消失，Si纳米团簇完全融化；在4000 K时，Si纳米更加聚集，将要突破SWCNT结构.

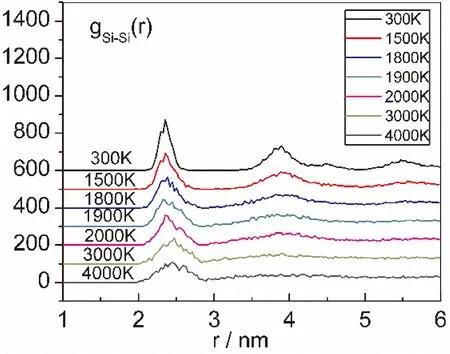
图4 复合结构中Si纳米团簇升温过程中g(r)曲线随温度的变化关系Fig.4 Relationship between g(r) and temperature in the heating process of Si nanoclusters of complex constructure

3.3 可视化分析

通过可视化软件观察到在图中Si-20团簇在(16,16)SWCNT中在300 K-1500 K时一直很稳定，并且团簇与团簇之间不发生反应，相互之间存在分子间的范德华力，使其不能靠得太近.当温度升高到1500 K时，Si-20团簇分子开始不稳定，两种团簇分子表面开始接触，内部的正十二面体依旧维持比较稳定的正十二面体形态.当温度继续升高到1800 K时，Si-20分子团簇继续靠近，观察到内部结构的Si-20结构开始变形，但整体结构没有大的变化.随着温度的继续升高，Si-20分子团簇之间完全接触，相互之间发生融合，外部和内部结构均被破坏，已不能有效的观测其形貌.

图5 不同温度下Si-20的结构变化 Fig.5 Constructure evolution of Si-20 with the changing of tempreature

3.4 Si-20 团簇在SWCNT的键角分布函数

键角分布函数可以描述每个原子与近邻原子的统计平均数.如果体系中有特定的结构，则可以通过特定的角显示出来.因此，键角分布函数能够反映出一些特定结构的变化.从图6可以看出：在300 K驰豫下，第一峰主要在109°28′附近，是典型的金刚石结构;随着温度的升高，第一峰开始变得平缓并且峰值左移，表明正四面体结构在慢慢地减少;温度持续性升高，Si纳米团簇逐渐融化，金刚石结构逐渐被破坏，此时Si原子周围聚集更多的原子，每个原子与近邻原子的键角统计平均变小.在完全融化的条件下，Si的键角该峰值依旧没有低于90度，这和Si原子的sp3杂化有关.

Fig.6 Bond angle distribution of Si nanoclusters under different temperatures图6 不同温度下Si纳米团簇的键角分布图

3.5 Si-20团簇在SWCNT的二面角分布函数

Fig.7 Dihedral angle distribution of Si nanoclusters under different tempreatures图7 不同温度下Si纳米团簇的二面角分布图

二面角分布是用来描述互为近邻的一对原子以及各自其他近邻原子所组成的二面角的统计平均情况，二面角分布的变化可以反映一些微观结构的变化.将二面角与键角分布函数结合起来可以表征更加广泛的结构.由于本实验中的原子个数比较少，只有3964个，且只统计了当中包含的700个Si原子，所以统计出来的二面角分布函数不是特别光滑.300 K时结构比较明显，主要分布在60°,120°,180°，这是正四面体的结构特征，到了1500 K几个主要峰值开始变得平滑，但还是存在，说明还存在少量的的正四面体结构，到了1800 K之后，可以看出来曲线开始慢慢变得平稳，看不出主要峰，说明很少或不存在正四面体结构.

3.6 对模拟结果的讨论

由于硅和石墨烯是不发生反应的，而CNT是通过石墨烯卷曲而成的，可以认为硅和CNT之间的反应是呈惰性的，二者之间不发生化学键反应，仅仅存在分子间的范德华力.而异构Si-20团簇之间也存在分子间的相互作用，使得Si团簇间，团簇与SWCNT之间始终存在的一定的安全距离，且SWCNT对Si纳米团簇还起着一定的空间限制作用.随着温度的升高，由于SWCNT的熔点比Si的高，所以在反应过程中，Si纳米团簇融化并相互之间结合在一起.部分Si原子会连续碰撞SWCNT的管壁，对SWCNT壁产生一个向外的压强，加之高温下SWCNT发生热振动，会加速C-C键的断裂，从而导致SWCNT的融化.