思维导图在初中数学《特殊平行四边形》复习课中的高效应用

黄晓丹

【摘要】自课改以来，教师一直在努力突破传统的教学组织形式，想方设法地改进和优化自己的教学方法和手段，绞尽脑汁地研究和探索课堂教学策略，并想借助多媒体的应用，给学生创造良好的课堂氛围，努力为学生提供高效学习的课堂。初中数学的高效课堂不仅要求教师要有好的教学策略，还非常注重学生的学习思维和行为的改变，但这点也需要教师正确、有效地引导，如果引导者能在课堂上引导他们正确把握关键的内容，找到主要内容的关联，并将它们之间的关联用你思维导图画出来，那么将会提升课堂教学效率。

【关键词】教学策略;高效课堂;初中数学;思维导图

思维导图最早是由英国学者Tony  Buzan在1970年早期所创，它以直观、形象的特点，受到人们的喜爱，它不仅在其他行业里呼风唤雨，还在教育行业里叱咤风云、来去自如，特别是在教学课堂上，虽然教师与思维导图之间的关系还不是很融洽，但这完全不影响教师对它的热衷和喜爱，所以，现在越来越多的教师将思维导图运用到教学课堂中，以此达到提高课堂教学的效率和学生学习的效率。而复习课是教师将已经授完的内容再现的一种教学方式。根据本校的学情，大部分学生也许能回忆起来，但能将这些学过的内容综合起来融会贯通使用的学生寥寥无几。如果在这里教师能利用思维导引导学生把各知识点联系起来，完善学生的认知结构，这样能有效地促进学生形成新的解题思想方法，教师在数学复习课堂里运用思维导图构建学生的知识结构，对学生的解题能力的优化、学生思维的建构能起到一定的作用，从而提高课堂的教学效率。

在众多题型中，几何证明题是学生较难掌握的重点内容之一。有些学生遇到几何证明题就像老鼠遇到猫，往往不知道从何下手，而有些学生知道它的结果，却不知道如何来叙述，这就需要教师的有效引导，如果学生在做几何证明题的时候，能对求解过程中每一个步骤的来龙去脉搞清楚了，那么，几何证明题的求解将会迎刃而解。本文将从北师大版九年级上册第一章《特殊平行四边》的复习课里阐述教师如何运用思维导图的方法帮助学生解决几何证明的求解难题。

一、要善于抓住课堂导入这一环节，运用思维导图把已学知识梳理成一个框架

课堂导入是教师在上课的开始的那几分钟要进行的一项教学活动，它通常出现的时间只有5分钟左右，如果教师能在这短短的5分钟里顺利“勾住学生的魂”，将会提高学生学习的效率和课堂教学的质量。

在“特殊的平行四边形”这节复习课的导入环节，教师可以让学生在一张白纸上根据自己理解梳理出本章所学内容，如果学生能画出大概的关系图，说明学生对这一章的基本性质、判定定理和基本知识点间的联系已经掌握，如果有学生不能很好地梳理出来，教师可以让已经画出关系图的学生上台展示成果，帮助这些学生回忆起已学知识。在导入这个环节利用思维导图梳理出整章知识点之间的联系，可以让学生快速地回忆起学过的内容，并在头脑里形成整章知识点的框架，能使学生的思维迅速定向，集中探索知识的本质，为学生后面解决综合性证明题提供了基础思路。结合学生画出的关系图，做出本章中菱形、矩形、正方形和平行四边形之间的关系图如下：

二、在解决问题时，运用思维导图帮助学生理清解题思路

初中阶段的几何题的证明基本上都是由已知和求证两部分组成。已知条件的意思就是求解证明题的前提条件，求证目标就是证明题最终要达到的目的。所以，求解证明题的过程就等于是给出一系列的前提条件，让你根据所学的几何性质、判定定理去找寻各个子目标，最终达到目的的过程。而很多学生在做几何证明题的时候，往往读完题目后还没弄清楚题目的意思，导致一遇到几何证明题就一筹莫展、无从下手。没有适当的解题思路是其中一个重要的原因，其实根据几何证明题的结构，解几何证明题的关键主要是掌握解证明题的一般思路，然后利用这些思路去探究解证明题的一般思维方法。

在“特殊平行四边形”这节复习课里，教师在讲解平行四边形的综合性证明题的时候，可以利用思维导图来帮助学生理清解题思路，在帮助学生理清思路的时候可以从以下几个思考方向。

（一）正向思维

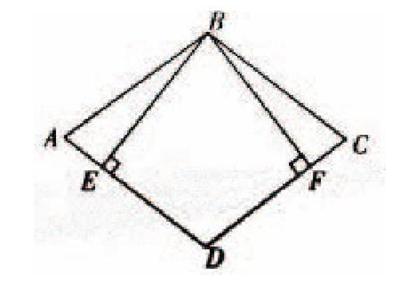
当我们遇到较简单的几何证明题的时候，我们可以直接正向思考，就是从原地出发，根据题目给出的一系列提示，逐关突破，最终到达目的地。例如，如图，四边形ABCD是菱形，BE⊥AD，BF⊥CD，垂足分别為E，F，求证：BE=DF。

在这道题里，教师就可以从正向思维出发直接从已知条件得到结论，从而达到最终目的。做出正向思维的思维导图如下：

从上面的关系图里，我们可以清晰、直观地看出本道题的解题思路步骤，此时学生再来写出证明过程，是易如反掌的事情。

（二）逆向思维

当我们遇到比较难的证明题的时候，往往不能一下子就能从已知条件得出结论，那么，此时我们可以从目标入手，也就是从求证的结论出发往反向推敲，从而达到目的。例如，如图，在正方形ABCD中，点E是CD的中点，点F是BC上的一点，且∠AEF=90o，延长AE交BC的延长线于点G。求证：AE平分∠DAF。

对于一些基础和思维比较活跃的学生来说，这道题根本没什么难度而言，但是像几何知识基础比较薄弱的学生来说，遇到这种题目，可能会不知所措，到底应该怎样来证AE平分∠DAF呢？对于这些学生可以用逆向思维来思考问题，即从结论“AE平分∠DAF”入手，要证明某条线段平分一个角，只需确定这条线段分的这两个角相等即可。做出的思维导图如下：

在这里从逆向思维出发，往回推敲出只要∠DAE=∠FAE，就可以证出AE平分∠DAF，而要证出∠DAE=∠FAE，就要证出∠FGE=∠FAE，我们可以从正向思维的方式从已知条件证出∠FGE=∠FAE，不管是基础较薄弱的学生还是中上学生甚至是优等生，在看到这个思维导图的解题思路以后，都能写出证明过程了，从而提高学生的解题效率，最终就能达到优化教学课堂效率的目的了。

思维导图作为一种全新的形式运用于教学中，改变了教师和学生传统的思考方式和解题思路，如果运用得好，这将会在很大程度上提高学生的逻辑思维能力，也能活跃课堂氛围，从而实现高效的课堂这一目的。当然，要实现高效的课堂不仅只有通过思维导图这一种方式，还有很多很多先进的教学工具和很好的教学策略，为了实现高效的课堂，教师要有不断学习、培训的意识，多“走出去”，学习外面的新理念，利用各种可利用的资源，结合本校学生的学情，找到适合自己和学生的教学方法。

[本文系河源市2018年中小学（幼儿园）教学研究课题“思维导图在初中数学课堂教学的实践研究”（课题编号：hy18062）的阶段性成果]

参考文献：

[1]秦学兴.谈谈如何构建初中数学高效课堂[J].教学·信息，2019（41）.

[2]沈东艳.思维导图在小学数学复习课中的应用研究[J].教育科研，2019（34）.