数学问题解答

2020年3月号问题解答

(解答由问题提供人给出)

2531设两个正数x,y满足xy=1,求证:

①

(天津水运高级技工学校 黄兆麟300456)

证明利用条件xy=1及权方和不等式,可得

即链①中第一个不等式成立.

再证明链①中第二个不等式.

由条件xy=1易知x+y≥2,

那么通分再去分母可得

⟺(x+y)(10+3x+3y)

≥(x+y+2)(2+3x+3y)

⟺6+10(x+y)+3(x2+y2)

≥10+8(x+y)+3(x2+y2)

⟺x+y≥2,

即链①中第二个不等式成立.

最后证明链①中第三个不等式.

即链①中第三个不等式成立，故不等式链①成立.

2532如图，已知梯形ABCD，且△ABC为等腰直角三角形，作PD⊥BD、QD⊥DC且△PDB∽△QDC，PM⊥AD，R为PQ中点，求证：AB∥RM.

(江西师范高等专科学校 王建荣 335000)

证明作AN⊥BC交BC于N，延长PM交BC于H，连DH，作TD⊥BC交BC于T并延长交PQ于R′，由∠PDR′=∠DBC,∠R′DQ=∠DCB，

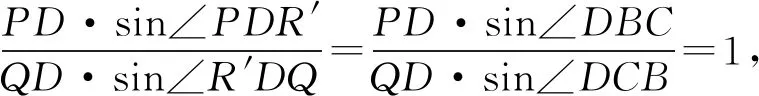
故R′P=QR′，因此R、R′重合，

由PH∥RT⟹S△MDR=S△PDR，

由P、B、H、D共圆

⟹∠PBD=∠MHD⟹△DMH∽△QDC

所以MD=RD⟹AB∥RM.

2533已知在锐角△ABC中，a2cosBcosC=9bccos2A,求cos3A的取值范围.

(安徽省六安第二中学 陶兴红237005)

解由a2cosBcosC=9bccos2A和正弦定理，

得sin2AcosBcosC=9sinBsinCcos2A,

即tan2A=9tanBtanC.

因为A+B+C=π,所以B+C=π-A,

所以tan(B+C)=tan(π-A),

即tanB+tanC=tanAtanBtanC-tanA,

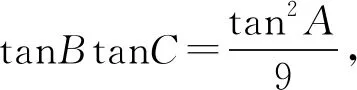
由均值不等式得

设x=cosA,y=cos3A,

则y=cos3A=4cos3A-3cosA=4x3-3x,

y=4x3-3x单调递减，

(浙江台州市洪家中学 邬天泉318015)

证明我们先证结论：已知抛物线Γ：y=ax2+bx+c，(a≠0). 单位圆⊙O：x2+y2=1.在抛物线Γ上任取三点A、B、C， 若直线AB、AC均与⊙O相切，则直线BC也与单位圆⊙O相切的充要条件为(a+c)2=b2+1.

设抛物线y=ax2+bx+c(a≠0),其上三点A、B、C的坐标分别为 (xi,yi)(i=1,2,3).

则直线AB的斜率为kAB=a(x1+x2)+b.

直线AB的方程为

y-y1=[a(x1+x2)+b](x-x1)，

即[a(x1+x2)+b]x-y=ax1x2-c.

直线AB与⊙O相切

⟺ (ax1x2-c)2=1+[a(x1+x2)+b]2；

同理，直线AC与⊙O相切

⟺ (ax1x3-c)2=1+[a(x1+x3)+b]2.

说明x2、x3是关于t的方程 (ax1t-c)2=1+[a(x1+t)+b]2的两个实根，

当|x1|=1时，直线AB或AC中必有一条为单位圆⊙O的垂直于x轴的切线，此时B或C中必有一个无穷远点.即为题设的极端情形.

当|x1|≠1时，则

则直线BC与⊙O相切

⟺ (ax2x3-c)2=1+[a(x2+x3)+b]2

⟺ [a(a-b+c)(x1-1)2+b2-(a+c)2+1]·

[a(a+b+c)(x1+1)2+b2-(a+c)2+1]

⟺ (a+c)2=b2+1.

结论成立.

通过坐标变换x=rx′，y=ry′，我们就可得到原结论.

(河南省南阳师范学院软件学院 李居之 孙文雪473061)

两边同除以ab+bc+ca，即得

当且仅当a=b=c时等号成立.

2020年4月号问题

(来稿请注明出处——编者)

(1)

当且仅当△ABC为等边三角形时式中等号成立.

(河南质量工程职业学院 李永利 467000)

2537若抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交，探讨以下问题：

(1)求过交点的直线围成的封闭图形的面积公式S(x),

(2)求面积公式S(x)的最大值，

图1

(3)如图1, 当四边形ABCD的面积取最大值时，求四边形ABCD对角线AC、BD交点P的坐标，并且探讨其几何性.

(安康学院数学与统计学院 赵临龙 725000)

(河南省方城县教研室 邵明宪473200)

2539已知⊙O1，⊙O2相交于P，Q两点，过点P的割线段AB交⊙O1于点A，交⊙O2于点B.两圆在A，B处的切线交于点S，直线SQ交△O1O2Q的外接圆于另一点T.求证：△O1O2P的外接圆直径等于线段ST.

(江西省高安市石脑二中 王典辉 330818)

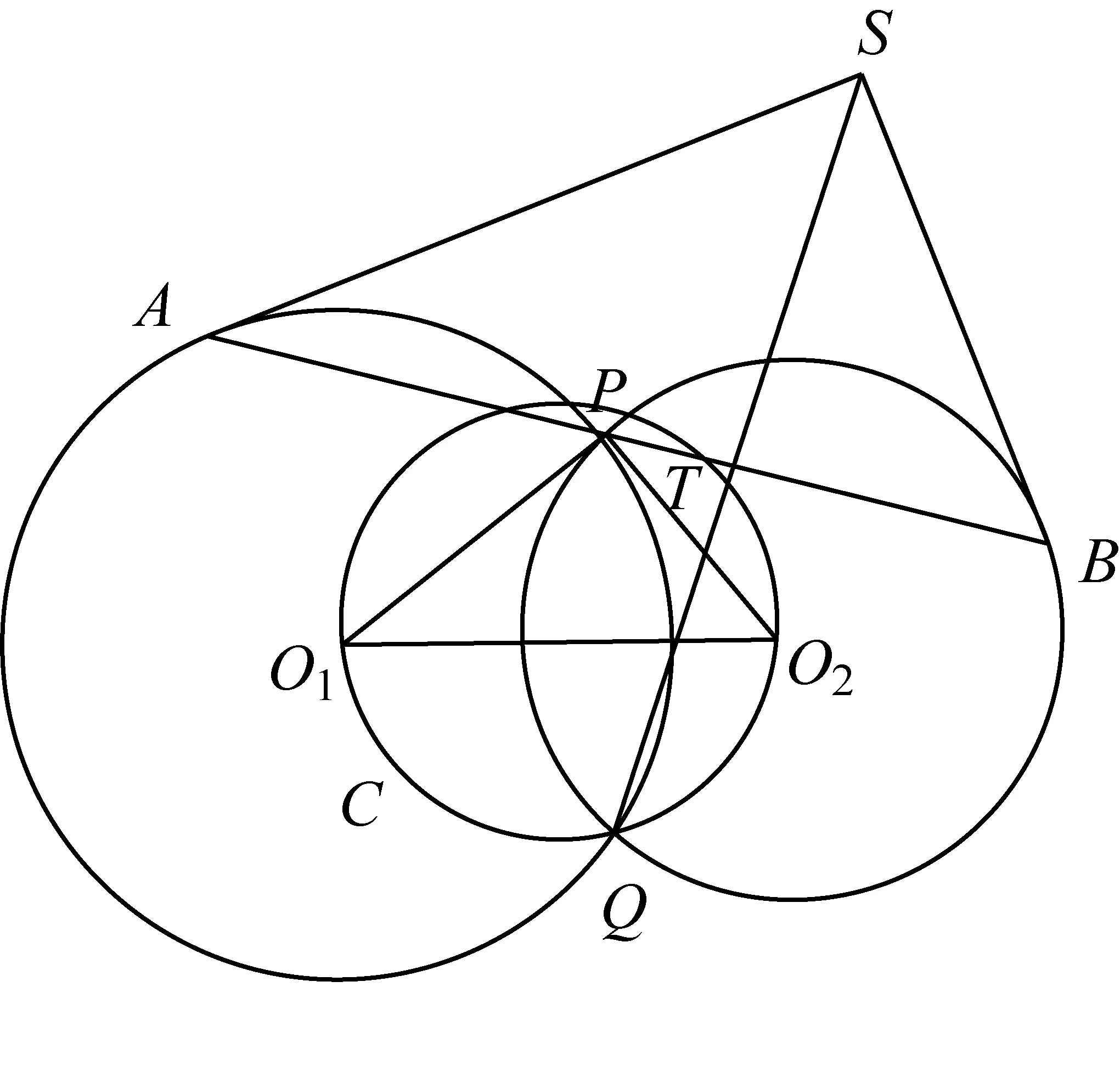
(四川成都金牛西林巷18号晨曦数学工作室 宿晓阳 610031)