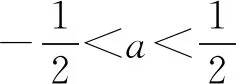揭示充要条件促进深度理解提升思维品质①

2020-05-11陶兆龙

数学通报 2020年4期

关键词：等价结论直线

陶兆龙

(江苏省南京市金陵中学 210005)

不注意揭示数学知识和方法中蕴含的充要条件，学生在对概念与方法一知半解的情况下进行机械学习在目前高中数学教学中较为常见.这种做法非常不利于学生数学核心素养的发展.

充要条件的学习对学生理解数学概念，掌握数学方法，提升思维品质有着很大的促进作用.新的课程标准已将充要条件提前到高一上学期讲授.借此良机，教学中应借助于充要条件，促进学生深度理解数学知识，发展学生的数学核心素养.

1 揭示数学概念定义中充要条件，促进学生对概念的深度理解

数学概念的定义与充要条件有着极为密切的关系，很多数学定义中都意味着一个充要条件．以适当的方式让学生认识到其中的充要条件是理解有关概念的关键．

在对数定义的教学中遇到过这样的窘境．在由特殊到一般地花费了一番周折，成功地引入对数定义后，让学生完成下列练习:

求下列各式的值:

(1)log232．

(2)log279．

有很多学生一脸茫然，不会算.

后来我们作了改进，在引入定义后，揭示了以下关系:

logaN=x⟺ax=N．(a>0，a≠1 )

依据这一充要条件不仅可以看到求对数值的“操作过程” (转化为指数)，还能进一步地认识到对数“结构对象”的属性:对数实际上是 “指数”，logaN就是表示实数a的多少次方等于N的那个数．

明确了这一充要条件后，学生就很容易想到求上述对数值的两种方法:转化为指数或直接由对数的意义求．

空间线面关系的定义就是判断相应线面关系的充要条件，既可以作为判定定理用，也可以作为性质定理用，以前的教学中，有很多教师在这方面处理得比较含糊，现在学习立体几何之前学生已经学习了充要条件，所以，引进概念的定义后，便可明确揭示相应的充要条件．

如线面垂直的定义:

如果直线l和平面α内的任意一条直线都垂直，就说直线l与平面α垂直，记为l⊥α．

由此可得:

直线l⊥α与平面垂直的充要条件是直线l垂直于平面α内的任意一条直线.

理解是应用知识的前提，对概念一知半解，灵活运用便无从谈起．揭示了数学定义中的充要条件，加深了学生对概念的理解，学生思维的深刻性得到了训练，为灵活运用概念奠定了基础．

2 揭示数学定理、公式、法则中的充要条件，促进学生对数学结论的深度理解

高中数学中的数学结论(定理、公式、法则)多数是以“若p，则q”的形式呈现，这里p是q的充分条件，其必要性有的具备、有的不具备.教材中因考虑到教学要求和学生接受能力等因素，多数未明确．在充要条件的概念提前到高一上学习以后，为用充要条件的形式来阐述数学结论提供了方便．明确数学定理、公式与法则中的条件对结论的充分性和必要性，不仅可以深化学生对数学结论的理解，还可以避免学生误用结论．

如学习等差数列{an}的通项公式后可引导学生得到: 数列{an}为等差数列的充要条件是存在常数k，b，使得:an=kn+b(n∈N*).

在单元复习阶段还可以揭示与等差数列的前n项和公式有关的充要条件.

设Sn是数列{an}的前n项和，则数列{an}为等差数列的充要条件是存在常数a，b，使得:Sn=an2+bn(n∈N*).

与公式有关的充要条件实际上揭示了等差数列的本质特征．揭示相关的充要条件，学生对相关知识的认识会上升到一个新的高度，同时还能学习体会到充要条件推证过程中运用的本单元的思想方法，这里有函数思想与递推思想等等．

数学结论中的条件有很多是充要的，也有充分非必要的以及必要非充分的，如不加以厘清，学生会将充分非必要条件或必要非充分条件当作充要条件．即将所有结论一视同仁，皆当成充要条件用．

揭示了有关的几个充要条件可以使学生深度理解基本不等式，避免错误运用，同时，还培养了学生思维的深刻性与缜密性．

3 揭示数学方法中的充要条件，促进学生对数学转化的深度理解

转化是解决数学问题最重要的、最基本的思维策略，转化意识与能力的强弱在一定程度上反映出学生数学核心素养的水平.解决问题的过程中，一般需要将问题的条件与结论进行转化，通常需要进行等价转化.等价转化实际上就是找到与条件或结论相对应的充要条件，从充要条件的角度揭示转化的等价性，可使学生更加深刻地理解解题过程中的转化策略，更加自觉地对条件进行充分必要的转化，或有意识地、灵活地进行充分非必要，必要非充分转化．

3.1 转化不充要是思维受阻的重要原因

在解决问题的过程中，有不少同学能够对条件进行不同形式的转化，得到很多关系式，但却无法找到解题思路.究其原因，往往是没有充要地转化条件．条件转化得不充分，自然就推不出结论．有的重复转化,没有对转化的充要性(等价性)进行分析,也会使思路陷入混乱.

问题1设点A和B为抛物线y2=4px(p>0)上除原点以外的两个动点，已知OA⊥OB，OM⊥AB，求点M的轨迹方程，并说明它表示什么曲线．

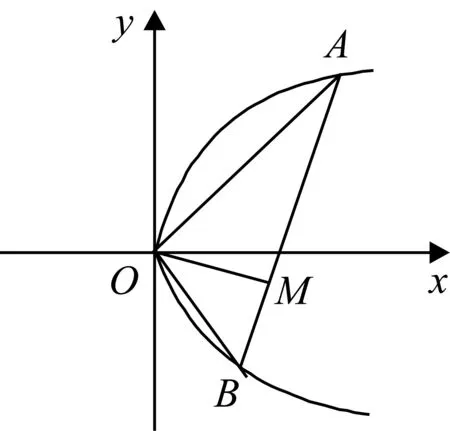
在解决这一问题时，有很多同学一会儿设出A，B两点的坐标，找出其关系；一会儿设出直线AB的方程，由方程组找关系，似乎有很多条件可以用，但又求不出轨迹方程.以下的情况极其常见.

从而y1y2=-16p2．

至此，解题中断．

同样，如用直线的斜率为参数，只要将条件充分必要地转化(等价转化)，便可以建立参数方程．如既用坐标参数，又用斜率参数，只要将条件充分必要的体现出来(转化)，也可以求出轨迹方程．

教学中，通过揭示条件转化的非充分性以及过度转化导致解题中断，让学生认识到解题思路的探索首先要对问题的条件进行充分必要地转化，这样做可以避免思维的盲目性，并为进一步探索指明方向.充分必要地转化所有条件是探索解题思路的基本策略.

3.2 揭示典型问题中的充要条件，深度理解等价转化

有不少典型问题的典型解法实际上已经将问题的条件进行了充分必要地转化，但解题过程中并没有给出明示，如不从充要条件角度揭示转化的等价性，学生则难以理解这些方法，这些基本方法的学习效果会大打折扣．

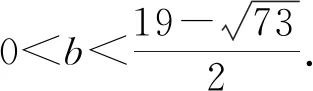
(b+9)x2-18mx+9m2-9b=0，

分析与解学生的一般的解法是，

(1)

两条曲线没有公共点,其代数表示即方程组无实数解．但这里,当0

这种错误解法和解决直线与圆锥曲线的位置关系如出一辙,是这一解法的负迁移．但这两类问题实际上是有区别的．

如直线y=x+m与椭圆4x2+y2=4有两个不同的交点,尽管椭圆上点的横坐标的取值范围是[-1,1],但并不需要讨论方程4x2+(x+m)2=4在[-1,1]上有两个不等的实根.因为,只要上述方程有两个不等的实根(Δ>0),由4x2=4-(x+m)2≤4知必有x∈[-1，1]．即此时, 在[-1，1]上有两个不等的实根的充要条件是方程在R上有两个不等的实根,两者是等价的．

这是由于直线方程和圆锥曲线方程的结构对转化后的一元二次方程解的范围有制约作用．在处理直线与曲线或曲线与曲线位置关系时,应对转化前后方程组和方程解之间的充要条件作出分析,以免学生机械模仿,不得要领．