通过探究性学习发展学生向量应用意识①

朱胜强

(南京外国语学校 210008)

1 问题的提出

向量是近代数学中重要和基本的概念之一， 它既是代数研究的对象，也是几何研究的对象，是沟通几何与代数的桥梁．自1996年进入高中数学课程以来，向量已成为高中数学的重要内容.为充分发挥向量的工具作用，2003年颁布的《普通高中数学课程标准(实验)》将平面向量与三角函数设计在一个模块中.《普通高中数学课程标准(2017年版)》则将相应内容纳入必修课程的主题三，名称上调整为“平面向量及其应用”，进一步强调了向量的工具作用.

然而，从多年教学实践所反映的情况看，学生对向量工具作用的认识似乎未达预期.在学习了平面向量之后，学生并没有具备良好的用向量工具解决问题的意识.在后续学习中，有许多可让向量发挥作用的时机，如两角差的余弦公式的推导，解析几何中直线与圆的方程的推导及多种解几公式的推导，正、余弦定理的推导等等，课堂上每遇这些内容的教学(包括一些公开教学活动)，任凭教师暗示、点拨，学生就是想不到向量，所学向量似乎仅限于在考试中取得相应的分数，这当然不是向量教学的目的所在.提高学生对向量工具作用的认识，增强思考问题时自觉运用向量工具的意识，应是向量教学中需要关注的问题.

回观向量教学，以苏教版教材为例，在介绍向量概念及其运算的同时，也渗透了向量的各种应用.既有物理背景的，也有平面几何、解析几何背景的.最后，还专门有一小节介绍向量的应用.但由于课时所限，如配套的教学参考书中，对平面向量一章的建议课时是12课时.学习过程中，学生的主要精力会集中在熟悉向量的各种运算上.等到对向量全貌有了基本认识后，却又要开始新章节内容的学习.因此，学生的向量应用意识的淡薄也就不足为怪了.

要巩固向量教学的效果，让学生感受到向量有用，自然可以在后续学习中有意识地搭建新知识与向量联系的桥梁.不过，这样做带有较大的随意性.除此之外，也可趁热打铁，在学生掌握了基本的向量知识之后，引导学生开展探究性学习活动，让他们在原有基础上及时获得更深刻的体验.

2 探究问题的设计

注意到向量兼具代数与几何双重属性，平面几何又是学生具备一定的基础，且是许多学生比较感兴趣的内容.因此，在内容的选择上，可考虑以平面几何问题为研究载体.虽然某些平面几何知识可能已淡忘，但对一些典型问题学生仍会留有印象.比如，在向量章节例、习题中涉及三角形重心、垂心、外心等问题时，学生不仅未感到陌生，而且觉得比其它问题更有趣.所以，从向量的角度对三角形的“四心”进行研究，既可顾及学生的现有基础，契合他们的兴趣爱好，也是对向量应用的一种自然地拓展延伸.

学生只有切实感受到向量工具的长处，才能提高应用的自觉性.初中平面几何属于欧氏几何，解决问题时只依据基本的逻辑原理(同一律、矛盾律、排中律等)，从基本事实(公理)出发，通过演绎推理，建立几何关系.因此，它给出的几何论证十分严谨，但往往无规律可循，存在较大思考难度.用向量工具研究几何问题，则是建立了向量运算(运算律)与几何图形之间的关系，对图形的研究借助代数运算来实现.

向量工具解决问题的第一个优点是所依据的定理法则少.高中阶段，向量法解决问题的基本法则只有4点:

法则2向量数乘的意义和运算律，特别是可以用数乘一个向量来表示和它平行或共线的向量；

法则3向量的内积(数量积)的意义和运算律，特别是互相垂直向量的内积为0；

法则4平面向量基本定理:如果e1，e2是平面内两个不共线的向量，则对平面内任一向量a，存在唯一的实数对λ1，λ2，使得a=λ1e1+λ2e2．

向量工具解决问题的第二个优点是思考方式有章可循.用向量方法解决平面几何问题，通常遵循如下“三步曲”:

(1)建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题；

(2)通过向量运算研究几何元素之间的关系，如距离、夹角等问题；

(3)把运算结果 “翻译”成几何关系.

从学生的角度看，向量的线性运算、数量积运算及平面向量基本定理都是他们已经掌握了的.解决平几问题“三步曲”中，学生最擅长的是第二步，向量运算.较为困难的是第一步，即用向量表示几何元素.因此，在进行探究问题设计时，应着力于学生的薄弱环节.

由此，考虑到了将探究问题设计侧重于用向量表示三角形的四心，进而提出如下问题:

3 探究过程与结果

设计的探究问题在进行“向量的应用”教学时给出，供学生课外研究.学生可以自由组合，也可以独立研究.可以选择三角形“四心”中的某一个心，也可以对所“四心”展开思考.约定好时间在班级数学学习群中交流探究成果.

问题给出后，学生意识到，依据平面向量基本定理，与三角形四个心所对应的向量应该能用基底表示.但具体怎么表示？都觉得问题并不像教材例、习题中类似问题那样简单，有一定的挑战性.

探究的过程中，有些学生遇到难以逾越的障碍，教师给予适当的指点，并提出一些建议.在截止时间到来的时候，参与探究的学生公布了各自研究的成果.

最后，学生推举出了几位代表对集体探究成果做进一步加工、整理，形成了如下大家认可的探究结论.

3.1 重心的向量表示

图1

因为G是AD，BE的交点，

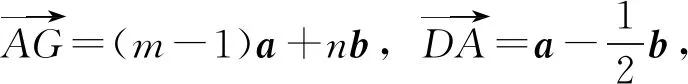
3.2 垂心的向量表示

图2

=(m-1)a+nb，

=ma+(n-1)b.

因为AHCB，BHAC，

这是一个关于m，n的二元一次方程组，可解得

可以看出，

为此考虑

[(b2-a·b)a+(a2-a·b)b]·(b-a).

由于

[(b2-a·b)a+(a2-a·b)b]·(b-a)=

(b2-a·b)(a·b-a2)+(a2-a·b) (b2-a·b)

=0，

3.3 内心的向量表示

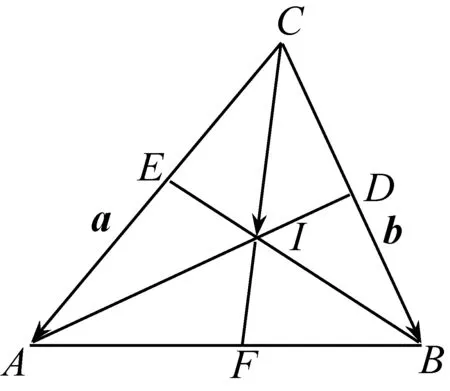
图3

= (m-1)a+nb.

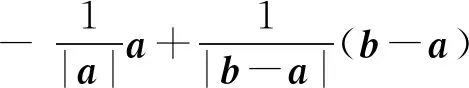
由向量共线定理可得

同理

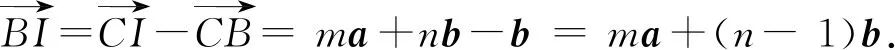
所以由向量共线定理可得

考虑关于m，n的二元一次方程组

所以

即CI是∠C的平分线.

所以，三角形三条角平分线交于一点.

3.4 外心的向量表示

图4

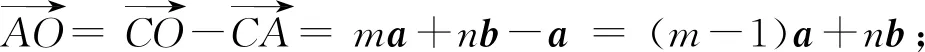
因为O为△ABC的外心，设外接圆半径为r，

所以 |(m-1)a+nb| =r；

|ma+(n-1)b| =r；|ma+nb|=r.

将上面三式两边分别平方，可得

(m-1)2a2+2(m-1)na·b+n2b2=r2；

①

m2a2+2m(n-1)a·b+(n-1)2b2=r2；

②

m2a2+2mna·b+n2b2=r2.

③

③-①得 (2m-1)a2+2na·b=0；

③-②得 2ma·b+(2n-1)b2=0.

得关于m，n的二元一次方程组

所以

4 探究成果的再应用

开展本次探究性学习的目的在于发展学生的向量应用意识，因此，获得探究结论并不是活动的终极目标.对结果与结果产生的过程进行再思考，有利于进一步深化学生对于向量工具作用的认识.

从获得的探究结果看，三角形的每个心所对应的向量确实都能用给定的基底表示，尽管有些结果获得的过程需经过一定量的运算，但这些运算的思路都是明确的.这可从一定层度上消除学生对于平面向量基本定理的神秘感.认为定理只是理论上可行，实践上怎么操作并不清楚.会用基底表示向量，便开启了向量工具应用之门，可有效提升学生利用向量工具的自信心.

从解决问题的过程看，所涉及的向量知识只局限于线性运算、数量积运算及相应的运算律，平面向量基本定理.且对于三角形不同的心，解决问题的思路也基本一致.

(1)将三角形某心对应的向量用基底线性表示，其中带有待定的参数；

(2)利用三角形某心的几何特征，得到关于参数的方程组.这里的几何特征主要是三点共线、互相垂直、角的相等、距离相等这些最基本的、简单的几何关系；

(3)解方程组，求出参数，实现将三角形某心对应的向量用基底表示.

在用基底表示出重心、垂心、外心后，还顺便用向量法验证了这些心分别是三角形的三条中心、高线、角平分线的交点.所涉及的向量知识依旧是向量共线、向量垂直等简单知识.从向量应用的角度对探究过程进行剖析，可以让学生切实体会到用向量在解决问题过程中的优势所在.

上述探究活动也可以作为深入开展探究性学习的新起点.当三角形的“四心”用基底表示后，可以很方便地研究一些与“四心”有关的问题，也可能激发学生主动提出一些新的问题.