圆外切四边形面积公式探索——从“2018年南京数学中考压轴题”谈起

程银生

(江苏省南京市南师附中新城初中黄山路分校 210019)

“结果如此巧合!”，“ 这仅仅是巧合吗？” 2018年南京数学中考压轴题以此亲切的口吻与考生对话，以聊天的方式“发现问题”、“提出问题”，引导学生“分析问题”、“解决问题”．命题者用心良苦，牵着考生的手，进一步，再进一步．笔者深受感染，沿着命题者指引的方向进行探索，现将发现呈现给大家，请多指导．

1 题目及解答

结果如此巧合!

下面是小颖对一道题目的解答．

题目：如图①，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积．

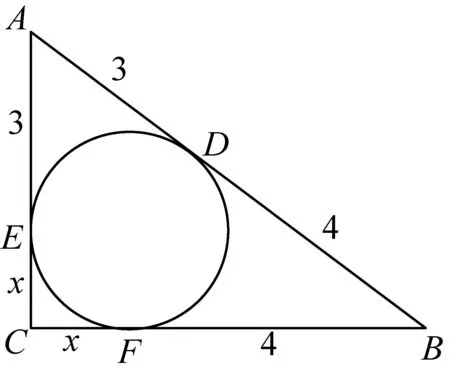
图①

解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x．

根据切线长定理，

得AE=AD=3，BF=BD=4，CF=CE=x．

根据勾股定理，

得(x+3)2+(x+4)2=(3+4)2．

整理，得x2+7x=12．

小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积．这仅仅是巧合吗？

请你帮她完成下面的探索．

已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n．

可以一般化吗？

(1)若∠C=90°，求证：△ABC的面积等于mn．

倒过来思考呢？

(2)若AC•BC=2mn，求证∠C=90°．

改变一下条件……

(3)若∠C=60°，用m、n表示△ABC的面积．

解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，

根据切线长定理，得

AE=AD=m、BF=BD=n、CF=CE=x．

(1)如图①，在Rt△ABC中，根据勾股定理，

得 (x+m)2+(x+n)2=(m+n)2，

整理得x2+(m+n)x=mn，

(2)由AC•BC=2mn，得

(x+m)(x+n)=2mn，

整理得x2+(m+n)x=mn，

所以AC2+BC2=(x+m)2+(x+n)2

=2[x2+(m+n)x]+m2+n2

=2mn+m2+n2=(m+n)2=AB2，

根据勾股定理逆定理可得∠C=90°；

(3)如图②，过点A作AG⊥BC于点G，

图②

在Rt△ABG中，根据勾股定理可得

=(m+n)2，

整理得x2+(m+n)x=3mn，

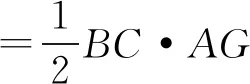
2 过程探秘

2.1 含60°角的三角形特殊化

△ABC的内切圆与AB相切于点D，AD=m，BD=n，∠C=60°．

当∠A=90°时(如图③)，I为△ABC的内心，四边形ADIE为正方形，

所以EI=AD=m，BF=BD=n，

图③

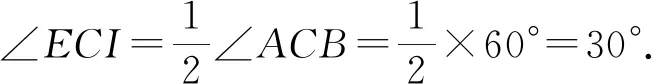
根据第(1)问结论，得

当∠A=60°时(如图④)，I为△ABC的内心，则AD=BD，

图④

2.2 结果猜想

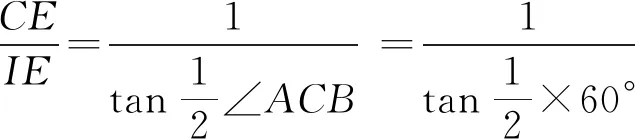
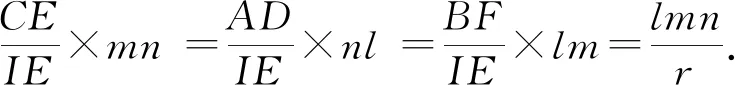
图⑤

(3)特例验证

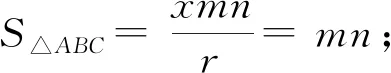
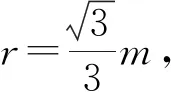
3 结论证明

△ABC的三边分别为a、b、c，内切圆与三边相切于点D、E、F(如图⑤)，AE=AD=m，BD=BF=n，CF=CE=l，⊙I的半径为r．

则l=p-c，m=p-a，n=p-b．

根据海伦公式

①

②

③

[三角形的面积等于三条切线长的积与内切圆半径的商]

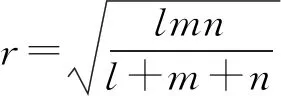
[三角形内切圆的半径等于三条切线长的积与三条切线长和的商的算术平方根]

4 结论拓展

4.1 三角形面积公式拓展

△ABC的内切圆I的半径为r，旁切圆J的半径为R，点D、E、F、G、H、K为两圆与三角形三边的切点 (如图⑥)，

AE=AF=a，BD=BF=b，CD=CE=c，CH=CG=d，AK=AG=e．

图⑥

那么△ABC的周长为2(a+b+c) ，

因为AB+AC+BC

=AB+AG+GC+BC

=BK+BH=2BK=2BH

=2(a+b+e) =2(d+b+c)，

所以a=d,c=e，

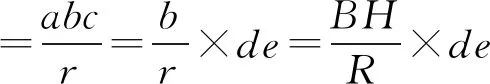
对以上结论可作如下呈现：

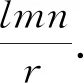
[文字语言：三角形的面积等于旁切圆的三条切线长的积与半径的商]

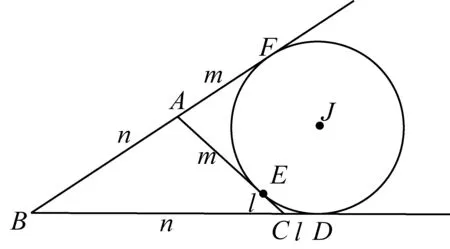
图⑦

4.2 圆外切四边形面积公式

四边形ABCD为⊙I的外切四边形，⊙I半径为r，点E、F、G、H为切点 (如图⑧)，AE=AH=a，BE=BF=b，CF=CG=c，DH=DG=d．设两对边DA、CB的延长线相交于点M，MH=MF=m．

图⑧

④

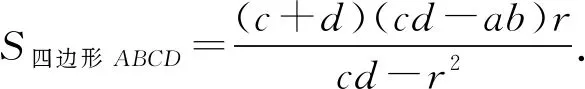
又因为S四边形 ABCD= (a+b+c+d)r，

所以(a+b+c+d) (cd-r2)= (c+d) (cd-ab)．

所以acd+bcd+c2d+cd2- (a+b+c+d)r2=c2d+cd2-abc-abd．

所以(a+b+c+d)r2=abc+abd+acd+bcd．

⑥

所以S四边形 ABCD= (a+b+c+d)r

⑦

[文字语言：圆外切四边形面积等于每三条切线长积的和与内线圆半径的商；也等于一边上两切线长与对边积加上这一边与对边两切线长的积的和除以内线圆半径的商]

由⑥式得四边形内切圆半径

上式代入⑦式，得圆外切四边形的面积公式

[圆外切四边形面积等于四条切线长的和乘以每三条切线长积的和的积的算术平方根]

特别地，当d=0时，即为海伦公式的变形①．

结语

G.波利亚说过：没有任何一道题是可以解决的十全十美，总剩下些工作要做．这里剩下的工作就是指解题反思，它可以优化解题过程，提高理解水平，训练数学思维……所以无论是学生还是老师都应该养成解后反思的习惯．正如此题，如果不反思，就只是两个三角形的面积问题，不可能出现一般三角形的情形，更不可能出现圆外切四边形的面积公式，结果的巧合，也仅仅是巧合而已．