“雨中行”的无风模型
2020-05-11刘晓曼保继光
刘晓曼 保继光
(北京师范大学附属中学 100052; 北京师范大学数学科学学院 100875)
“雨中行问题”来源于我们的生活实际,具体表述如下:下雨天在没有带任何雨具的情况下,人从一处到另一处,如何行走(此处把跑也看作行走的一种形式)才能减少淋雨量呢?在这种情况下,人们确实会选择快速行走的方式到达目的地,但越快淋雨量就越少吗?
1 已有的模型
1972年,Deakin在[1]中把人看成长方体,利用三维向量借助相对雨速的分解建立了有风时的雨中行模型.第二年,他与Schwartz对之前的数学模型进行了修改[2],纠正了原模型中的一个技术性错误,并简化和拓展了已有的结论,认为当顺风行走时,雨从背后吹来,当风的速度大于某一值时,以风在人行走方向上的分速度行走最佳,其他情况都应该”行走的越快淋雨量越少”.1976年,Bell也对此问题进行了研究,通过分速度建立了有风时的雨中行模型,并得出类似的结论[3].在20世纪九十年代中期,此问题广泛得到了气象界的关注和研究[4],其结果被总结为:当顺风行走时,以风在人行走方向上的分速度行走最佳;当雨迎面而来时,行走的越快越好.2002年,Bailey对此结论提出了质疑,认为上面逆风时结论是正确的,而顺风时要考虑风速度的大小,其通过分类讨论的方法并结合案例说明了,当风速较强时以风在人行走方向上的分速度行走最佳,但当风速较弱时,应该是行走的越快越好[5].此观点本质上是1973年Deakin和Schwartz结论的重述,都认为顺风且风速大于某一速度时以风在人行走方向上的分速度行走最佳,其他情况都应该越快淋雨量越少.
2000年,李志业在[6]中利用相对运动的速度合成理论得出“行走的越快淋雨量越少”.随后很多学者对此问题进行过研究,并且从不同的角度建立了相应的数学模型,得出了一些定性或者定量的结论.文[7]利用常微分方程分析得出“淋雨总量的多少与人的体型、雨速、行走距离有关系,胖人比瘦人淋雨多,高的比矮的淋雨多,并不是行走的越快淋雨越少,有时可能反而越多”这一定性结论.文[8]利用函数的单调性和极限得出与文[2]一致的结论.文[9]对人无风行走、逆风行走、顺风行走以及雨线方向和行走方向不在一个平面四种情况分别做了不同的分析,也得出了与文[2]一致的结论,只是研究思路上从特殊到一般且具体的分析了每种情况,呈现形式上更加适合中学生.
上述研究尽管方法和结论有些不同,但是在假设上同质性很高,大都对此现实问题做了以下假设.
假设1人在行走的过程中,雨始终以相同的速度和方向落向地面.
假设2人始终以恒定速度v做匀速直线运动,行走了固定距离D.
假设3人近似的看成是一个长方体,其中人体的正面宽度l,侧面宽度d.
无风的情况是最简单、最理想的情况,上述研究中只有文[9]将其单独研究,其余都是作为有风时的特例没有进行特殊说明.无风时雨是垂直落向地面的,淋雨总量等于降雨强度c(即单位时间单位面积的降雨量)、淋雨时间以及淋雨面积三者的乘积.人在无风的情况下行走时,淋雨区域只有人身体的上面,此时容易得到淋雨总量
(1)
由上述表达式,Q是一个关于v的反比例型函数,随着v的增加Q是减少的,也就是说“无风情况下人在雨中行走时,跑得越快淋雨量会越少”.
值得关注的是,2009年,Hailman与Torrents把淋雨者假设成椭球体模型,得出:顺风时如果雨水从背面吹来,人最佳的行走速度要略大于雨在人行走方向上的水平分量,并说明了人体形状在研究此问题时的重要性,同时说明了尽管都是椭球体模型,但人的体态也影响最佳行走速度[10].2015年,Seongtaek分别考虑了长方体、椭球体、圆柱体三种立体倾斜时的情形,利用其与雨的正交投影面积建立模型,找到人的最佳行走速度[11].
2 模型的优化
《流言终结者》(MythBusters)是一个美国的科普电视节目, 针对各种广为流传的谣言和传奇进行实验, 在探索频道(Discovery Channel)播出. 2003年9月, 在第一集《雨中行(Who Gets Wetter)》中就通过实验得出“行走得越快未必淋雨量就越少”. 参见https://v.qq.com/x/page/g0650smwg4p.html?fromvsogou=1.
本文对无风雨中行的情形进行优化. 我们注意到, 假设3反映的是人在雨中一动不动的情景(比如人在敞篷车上站立不动),因此上述模型的水平投影面积是保持不变的. 实际上根据人们的生活经验,当人运动时水平投影面积是变化的,并且随着速度的增加,摆动的幅度都会增加,投影面积从而也会增加,因此我们做出假设4.
假设4在行走时,人的水平投影面积S与行走速度v的关系设为
(2)
其中S0是人静止时的水平投影面积,k是一个待定常数,v0为人行走速度的一个上限.
此时无风时的总淋雨量
对Q关于v求导得


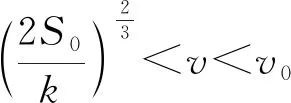


下面我们将近似确定S0、k,以期具体分析无风时淋雨总量Q随v的变化情况,探索人在雨中行的最佳策略.
1983—1987年,国家标准化主管部门开展了我国人体的测量工作,在全国东北、华北、西北、东南、华中、华南、西南等地区内共测量了11164名男子样本和11150名女子样本,并根据测量结果颁布了《中国成年人人体尺寸》(GB10000—1988)下表是人体水平尺寸中最大肩宽和胸厚的部分数据[12].
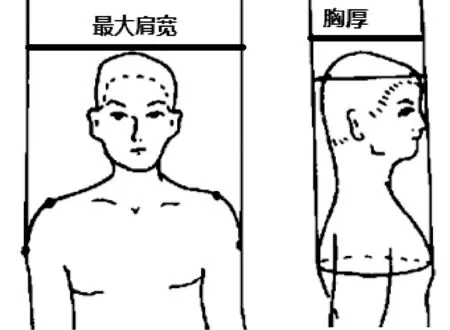
图1 最大肩宽与胸厚示意图

表1 中国成年人人体尺寸
注:所列数值代表从事工业生产的法定中国成年人,男18~60岁,女18~55岁.
为了计算的简化,我们采用矩形来刻画人体静止时的水平投影面积,投影面积为人体胸厚与最大肩宽的乘积.通过计算并保留四位小数可得下表.

表2 中国人静止时水平投影面积
由表2可知,中国成年男性静止时的水平投影面积最大分布范围为0.0674~0.1268m2,中国成年女性静止时的水平投影面积最大分布范围为0.0552~0.1191m2.综合可知,中国成年人静止时的水平投影面积最大分布范围为0.0552~0.1268m2.这就是S0的分布范围.
由表1可知,中国成年男性胸厚尺寸的第1百分位数为0.176m,第99百分位数为0.261m,相差0.085m,而第10百分位数为0.191m,第90百分位数为0.237m,相差0.046m. 因此数据中存在个别偏大或者偏小的数据,所以我们可以利用第50百分位数,也就是原始数据的中位数来刻画中国成年男性胸厚尺寸.同理利用第50百分位数来刻画中国成年男性最大肩宽尺寸,两者的乘积作为中国成年男性静止时水平投影面积的平均水平,即为0.0914m2,同理中国成年女性静止时水平投影面积的平均水平为0.0790m2.在下面的研究中我们可以将其作为(2)式中的S0.
下面确定(2)式中的系数k.由于人运动时水平投影面积的数据获得途径较少,所以我们进行了个案研究,以此获得k的数据.结合运动学的相关资料可知[13],人正常走路的速度平均为0.8m/s~1.5m/s,慢跑的速度平均为1.5m/s~4m/s.本文以正常行走和慢跑速度的数据分别进行模拟.
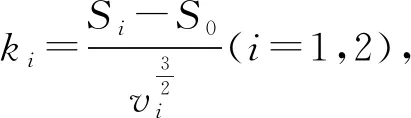
在此模拟测量中,为了方便,我们取正常走路的速度为v1=1m/s,慢跑的速度为v2=3m/s进行模拟.代入上述关系式中,求出k1与k2的平均值作为此志愿者的比例系数k,综合下面四名志愿者的比例系数作为本文假设4的系数k.
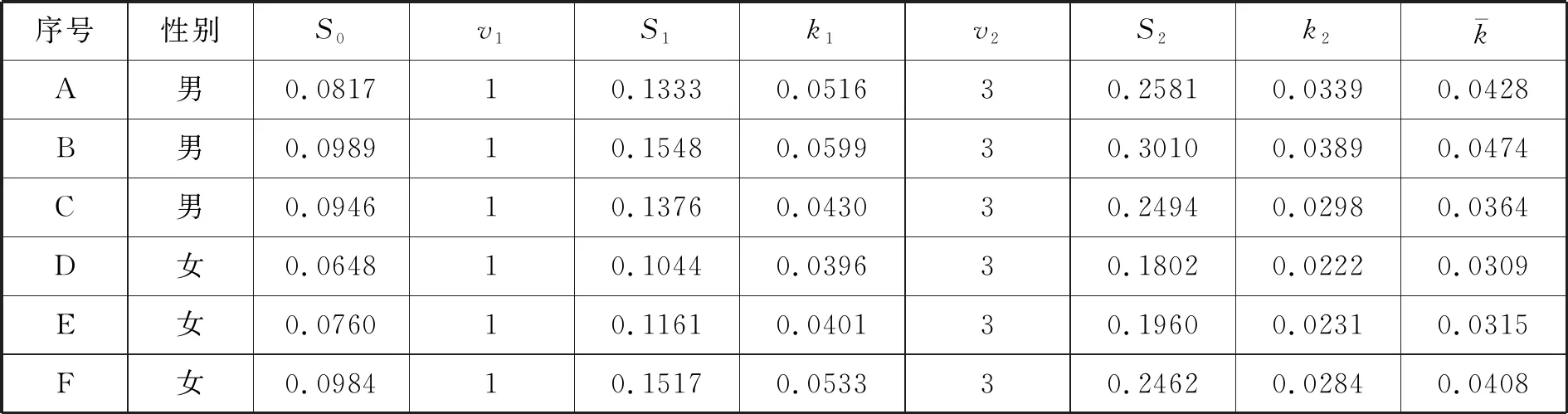
表3 模拟测量的数据
注:其中S0,S1,S2的单位为m2,v1,v2单位为m/s.
由上表志愿者数据可知,成年男性运动时水平投影面积的变化系数k的平均值为0.0422,成年女性运动时水平投影面积的变化系数k的平均值为0.0344.综合上面的分析,这里对成年男性、女性分别计算最佳行走速度.
查阅资料可知,男子百米短跑的世界记录为9秒58,平均速度不超过11m/s,因此有理由认为(2)式中v0=11m/s.对于中国成年男性,

从而v男 时,成年女性在无风的雨中行走淋雨量最少. 由于v男、v女的数值都属于慢跑范围,所以在无风的雨中行走时,慢跑相对来说淋雨量最小,并不是越快淋雨量越小. 图2 无风时成年男性总淋雨量Q模拟效果图 人静止时的水平投影面积S0,不同的国家差别较大. 前苏联测算的春秋季节成年人的平均尺寸为0.113m2;奥地利年龄在15~30岁未穿外套的人员水平投影面积为0.146m2,身穿外套时是0.186m2;德国的人员水平投影面积为0.120~0.190m2;美国18~45岁男女人员的平均水平投影面积为0.091m2. 因此S0的值受地域、民族、性别、年龄、体型等各种因素的影响[14].
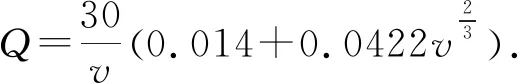

3 模型评估

