考虑变应力影响的粗糙裂缝油水两相流动能力数值模拟方法
2020-04-25王东英宋文辉
王东英, 姚 军, 宋文辉, 孙 海
(中国石油大学(华东)石油工程学院,山东青岛 266580)
低渗油藏、页岩油藏等非常规油藏普遍发育裂缝[1-5],且一般需要进行水力压裂实现有效开采[6-12]。裂缝的存在会改变储层中流体的流动特征[13-16],开展裂缝中油水两相相对渗透率及毛管力曲线的研究对指导裂缝性油藏开发具有重要意义。Huo等[17]和廉培庆等[18]分别测量了不同有效应力下,真实裂缝的油水相对渗透率曲线;Watanabe等[19]通过测量裂缝中油水的相对渗透率曲线,发现真实裂缝中两相流动存在较强的相互干扰性,提出了“V”型相对渗透率曲线。不少学者也已建立了描述单条裂缝中两相流体流动能力的解析模型。如Romm[20]提出的“X”型相渗模型;Brooks等[21]基于多孔介质推导的考虑两相间相互干扰的相渗模型;Fourar等[22-23]根据理想管流模型提出的考虑黏性力的相对渗透率解析模型。以上模型所依据的物理模型忽略了真实裂缝的复杂性,不能直接应用于数值模拟研究。较成熟的求解相对渗透率的解析模型,如Burdine模型[24]及Mualem模型[25],可用于考虑开度分布的粗糙裂缝相对渗透率曲线的求解[26],但过分依赖于模型参数取值,直接用于相对渗透率曲线的计算缺乏普适性。侵入逾渗模型考虑毛管力主导的稳态驱替/吸吮过程[27-28],已被不少学者应用到裂缝的两相流动模拟中[17, 29-30]。其中Ye等[30]采用侵入逾渗模型研究了裂缝中的两相流体相渗曲线,但模拟过程为吸吮,且模型没有考虑裂缝所受有效应力对流体流动能力的影响。笔者基于侵入逾渗模型,模拟单条粗糙裂缝中油水两相流体流动的稳态驱替过程,并讨论不同有效应力对裂缝开度分布及油水两相流动能力的影响,揭示真实裂缝在变化应力下的流动规律。
1 模拟方法
1.1 基本原理
侵入逾渗模型最初用于模拟孔隙网络模型孔隙及喉道中的驱替及吸吮过程[28],其中驱替过程取决于其喉道的大小,而吸吮过程由孔隙大小控制[31-32]。笔者着眼于低渗透油藏中重要的渗流通道——裂缝,基于侵入逾渗模型对单条粗糙裂缝内油水两相流动的毛管力和相对渗透率曲线进行研究。
采用蒙特卡洛模拟方法,在服从一定高斯分布规律的前提下,随机分布单条粗糙裂缝中的局部开度,流体流动为稳态驱替过程且遵循达西定律。初始时刻,裂缝被湿相流体饱和,逐步提高驱替压力注入非湿相流体,使非湿相逐渐进入更多的裂缝空间驱替湿相流体。本研究选取水相为湿相流体,油相为非湿相流体。
采用侵入逾渗模型来描述稳态驱替过程与规律,为求取油水两相相渗曲线,需先确定不同驱替压力下的油水界面移动过程及饱和度分布。编制程序搜寻某驱替压力下,与入口端相连的驱替相连通团的位置及编号得到油水两相分布,利用有限差分法分别数值求解水相与油相流体的压力场,最终,通过驱替过程中两相流体的有效渗透率与单相流动时绝对渗透率的比值获得两相流体的相对渗透率。
1.2 模型假设
基于CT扫描得到的真实裂缝图像获得裂缝开度数据[33],图1是由真实裂缝数据重构而成的粗糙裂缝形态及开度分布规律。经过数据分析发现,裂缝开度服从均值为580 μm、标准差为230 μm的高斯分布。

图1 真实单条粗糙裂缝形态及开度分布Fig.1 Real single rough fracture pattern and aperture distribution
为简化模型,考虑粗糙度的单条裂缝如图2所示。将裂缝区域进行离散,裂缝局部采用蒙特卡洛模拟方法随机赋予一定开度值,并使其整体服从高斯分布,同时认为离散后每个网格内部开度一致。出、入口端定压力,上下两端封闭,驱替过程流体流动方向从左至右,
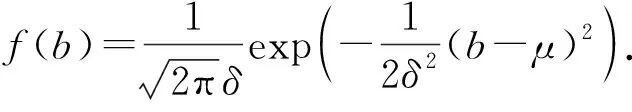
(1)
式中,f(b)为单条粗糙裂缝开度服从的高斯分布函数;μ为裂缝开度分布均值,m;δ为裂缝开度分布标准差,m;b为裂缝局部开度,m。
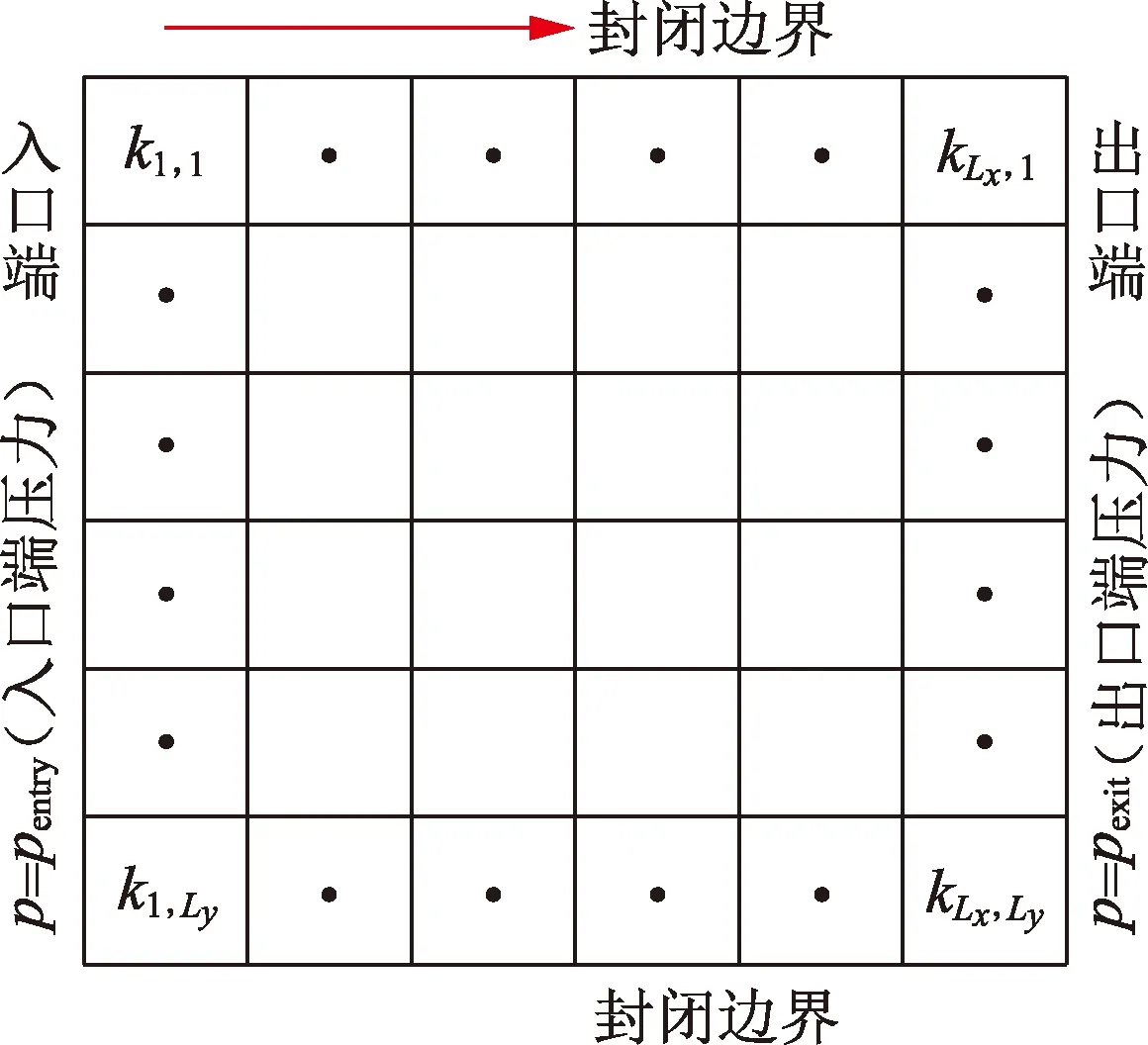
图2 单条粗糙裂缝模型示意图Fig.2 Schematic diagram of single rough fracture model
同时,模型假设:考虑二维平面流动,忽略垂向流动及重力的作用;油水两相不相溶,流动遵循达西定律;流体不可压缩,裂缝受有效应力作用可压缩;考虑裂缝内部的非均质性。
1.3 数学模型
首先,采用立方定律描述裂缝内局部渗透率,即
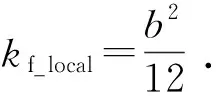
(2)
式中,kf_local(f=o,w)为裂缝内部局部渗透率,m2。
油相的连续性方程为
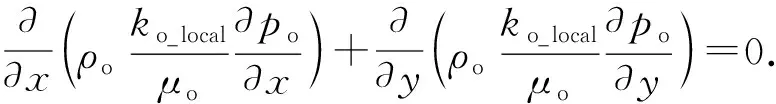
(3)
水相的连续性方程为
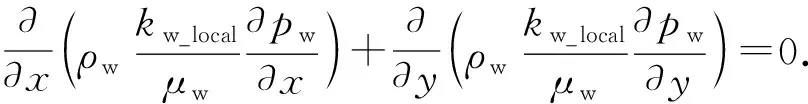
(4)
式中,ρo和ρw分别为油相和水相密度,kg/cm3;μo和μw分别为油相和水相的黏度,Pa·s;po和pw分别为油相和水相压力,Pa。
辅助方程为
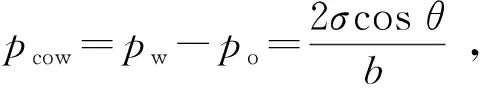
(5)
So+Sw=1.
(6)
式中,pcow为油水两相之间的毛管力,Pa;σ为油水界面张力,N/m;θ为水相接触角;So为油相饱和度;Sw为水相饱和度。
初始条件为
p0(x,y)=pi.
(7)
边界条件为
p(0,y)=pentry,
(8)
p(Lx,y)=pexit,
(9)

(10)
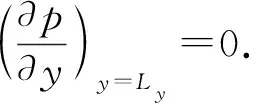
(11)
式中,p0(x,y)为初始时刻裂缝各处对应的压力,Pa;pi为裂缝初始压力,Pa;p(0,y)为裂缝模型左端(入口)压力,Pa;pentry为入口压力,Pa;p(Lx,y)为裂缝模型右端(出口)压力,Pa;pexit为出口压力值,Pa;Lx为单条裂缝模型长度,m;Ly为单条裂缝模型宽度,m。
综上所述,初中教师在开展化学教学的过程中,有目的、有意识的提高学生的科学素养是非常必要的。在此模式下,不仅可以展现出学科价值,使得化学教学更有意义,也能推动学生的全面、综合发展,为其后续的深入性学习打下基础。虽然,在当前,部分教师在此方面的意识还比较淡薄,但我确信只要在大家的持续努力下,一定能改善这一现状,促使我国的教育事业得以更加持续、稳定的发展下去。
基于侵入逾渗模型,判断不同驱替压力下的油水两相分布情况,此时含水饱和度与驱替压力关系即为毛管力曲线。采用有限差分方法数值求解上述方程得到油水两相流体的压力场分布,分别计算两相流体流量,得到相对渗透率,
(12)
(13)
(14)
式中,下标f为o或w;kabs_f为绝对渗透率,m2;Qf为油或水单相流动时的流量,m3/s;μf为油或水的黏度,Pa·s;A为单条粗糙裂缝的横截面积,m2;keff_f为油或水的有效渗透率,m2;qf为驱替过程中,油水两相流动时油或水的流量,m3/s;Kr_f为油或水的相对渗透率。
2 模型可靠性检验
2.1 模型构建
根据真实粗糙裂缝开度的高斯分布结果构建概念模型。单条粗糙裂缝物理尺寸为0.1 m×0.1 m,横截面积为5.86×10-5m2,模型中网格数为100×100,如图3所示。假设裂缝表面亲水,水相接触角为60°,界面张力取值0.048 N/m,油水两相黏度分别为15和1 mPa·s,模型整体处于大气压力环境,入口与出口压力差为10 Pa。
2.2 计算结果
结合侵入逾渗模型及上述基本参数对粗糙裂缝中油驱水过程的两相流体流动进行模拟。

图3 粗糙裂缝模型开度分布示意图Fig.3 Local aperture distribution of single rough fracture model
图4为驱替过程中的油水两相分布,其中红色代表油相,蓝色代表水相。驱替相即油相首先会进入连续的具有较大局部开度的位置驱替湿相流体,随着驱替压力逐渐提高,才侵入裂缝中更多开度较小的位置。
图5为数值求解得到的毛管力曲线和油水两相的相对渗透率曲线。由求得的相对渗透率曲线可以看出,对于考虑粗糙度的真实裂缝,若采用传统“X”型光滑裂缝相渗曲线来描述油水两相流动特征会造成较大误差。通过研究发现,当含水饱和度较高即驱替初始时,由于水相占据较大孔隙并连通,使之渗透率较高,而油相很大程度上为不连续相,因此渗透率极低。随着驱替过程的进行,油相渗透率升高,水相渗透率不断减小。当含水饱和度减小到一定值后,水相渗透率极低,这是由于裂缝表面亲水,水相被圈闭在不连续的极小孔隙中,不再具有流动能力。
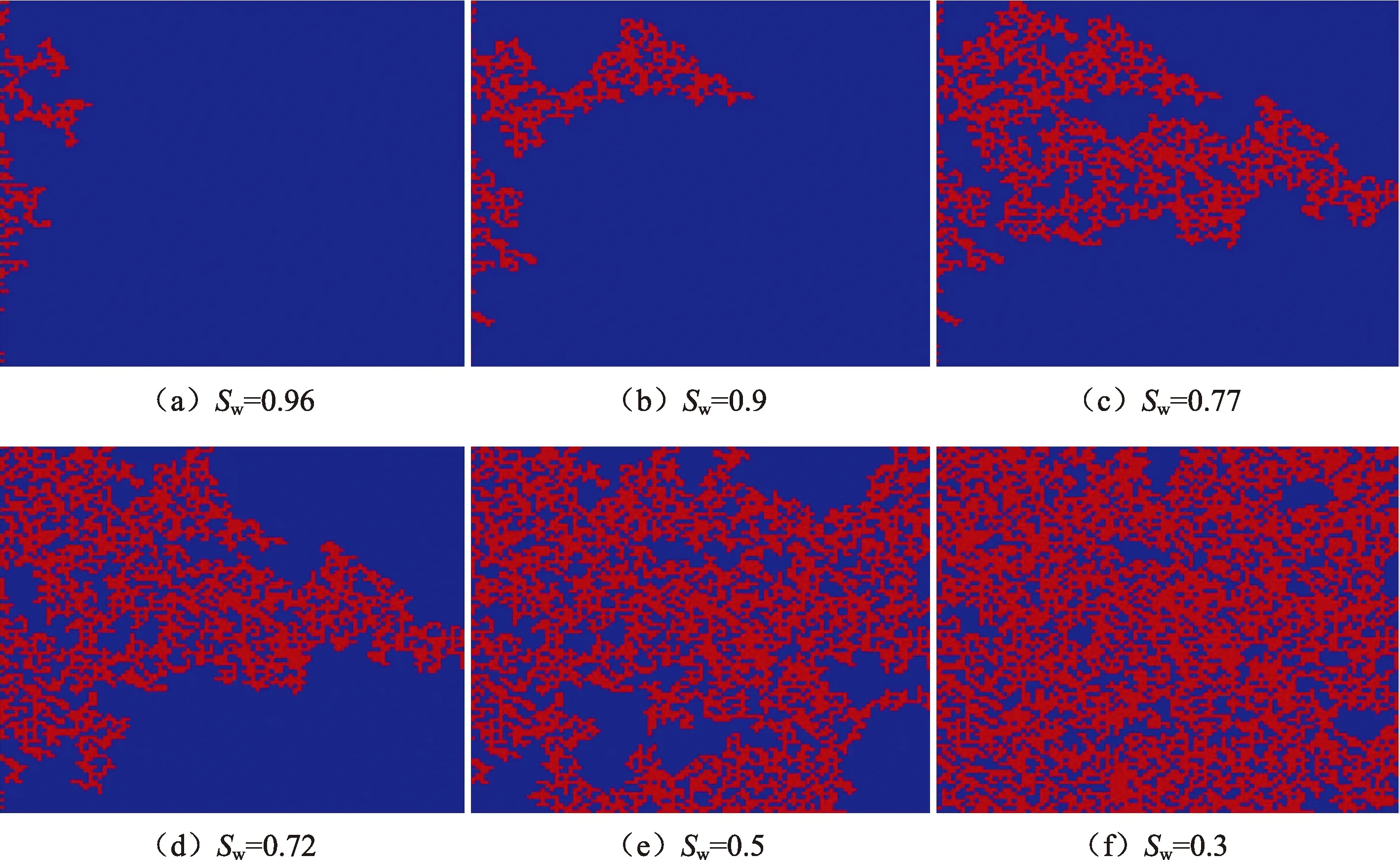
图4 驱替过程两相分布Fig.4 Two-phase distribution during displacement
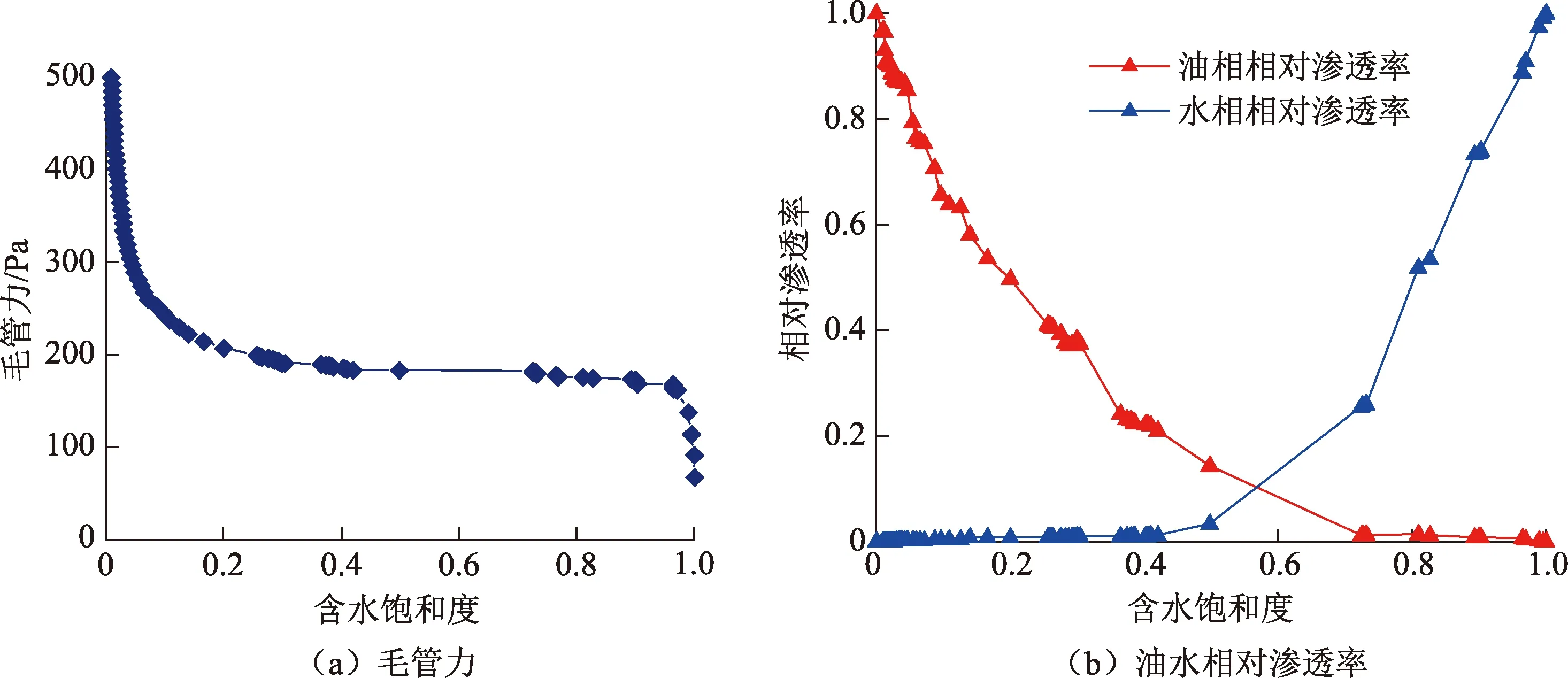
图5 毛管力及油水相对渗透率曲线Fig.5 Capillary pressure and oil-water relative permeability curves
2.3 模型验证
对比目前描述光滑裂缝相对渗透率的“X”型解析模型,Ye等[30]通过研究发现,Mualem模型可以考虑粗糙裂缝中的开度分布,并将水相与油相的有效饱和度与裂缝开度联系起来,从而对相对渗透率进行描述,因此采用Mualem模型与本文中的数值计算结果进行对比。根据Mualem模型,水相与油相的相对渗透率可表达为饱和度的幂律分布形式,
(15)
(16)
(17)

(18)
式中,Swe为水相有效饱和度;Swr为最小水相饱和度;Sws为最大水相饱和度;Soe为油相有效饱和度;Sro为最小油相饱和度;Sos为最大油相饱和度;Krw为湿相相对渗透率;Kro为非湿相相对渗透率;ηw为求解湿相流体相对渗透率时的经验系数,ηw=2.2;ηo为求解非湿相流体相对渗透率时的经验系数,ηo=2.1。
结合实例计算结果,将数值求解结果与上述Mualem模型进行对比验证,结果见图6。由图6可以看出,二者的计算结果表现出较好的一致性,验证了本文中数值模拟方法的正确性。

图6 模型验证Fig.6 Model validation
3 有效应力对裂缝内油水两相流体流动的影响
3.1 有效应力对裂缝开度分布的影响
裂缝性油藏在压裂及开采的过程中所受应力不断变化,相应的裂缝内部流体的流动也会受其影响。因此本文中采用Wu等[34]提出的描述单条裂缝开度与裂缝所受有效应力之间的解析关系,
b=bi+Δb=bi+(Δσ/κ) .
(19)
式中,κ为裂缝的刚度,κ=1×1011Pa/m;bi为裂缝初始局部开度,m;Δb为裂缝在不同应力条件下局部开度的变化,m;Δσ为裂缝所受的有效应力,Pa。
当有效应力为15和30 MPa时,单条裂缝对应的开度变化分别为150和300 μm。研究不考虑应力条件及有效应力分别为15和30 MPa时裂缝开度分布情况(其他参数取值均不变),由于裂缝开度服从高斯分布,有效应力变化后,裂缝开度整体减小并出现部分闭合的现象,图7、8分别为裂缝开度变化趋势及不同有效应力条件下对应的裂缝开度分布情况。
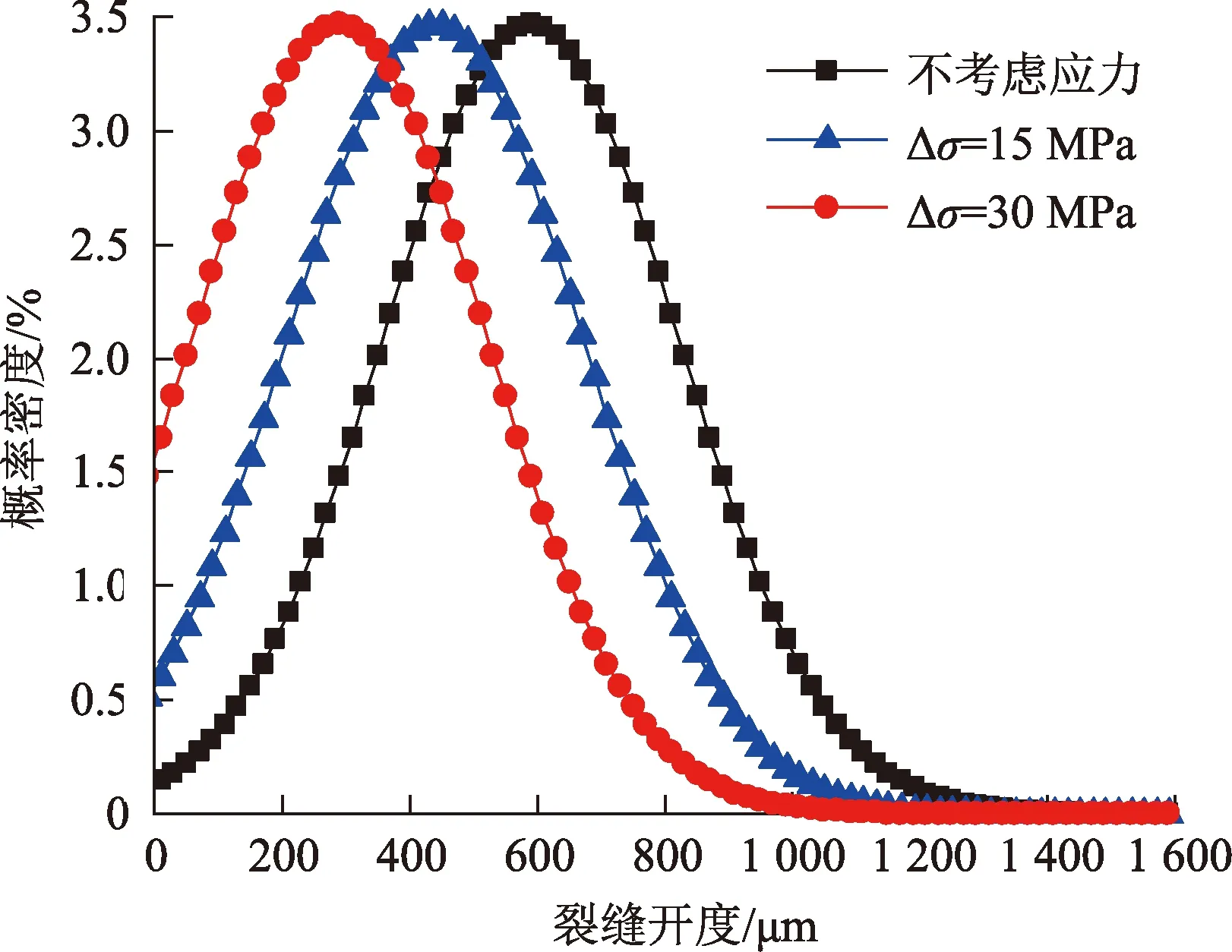
图7 不同有效应力条件下单条粗糙裂缝开度概率密度分布Fig.7 Aperture distribution in single rough fracture under varying effective stress
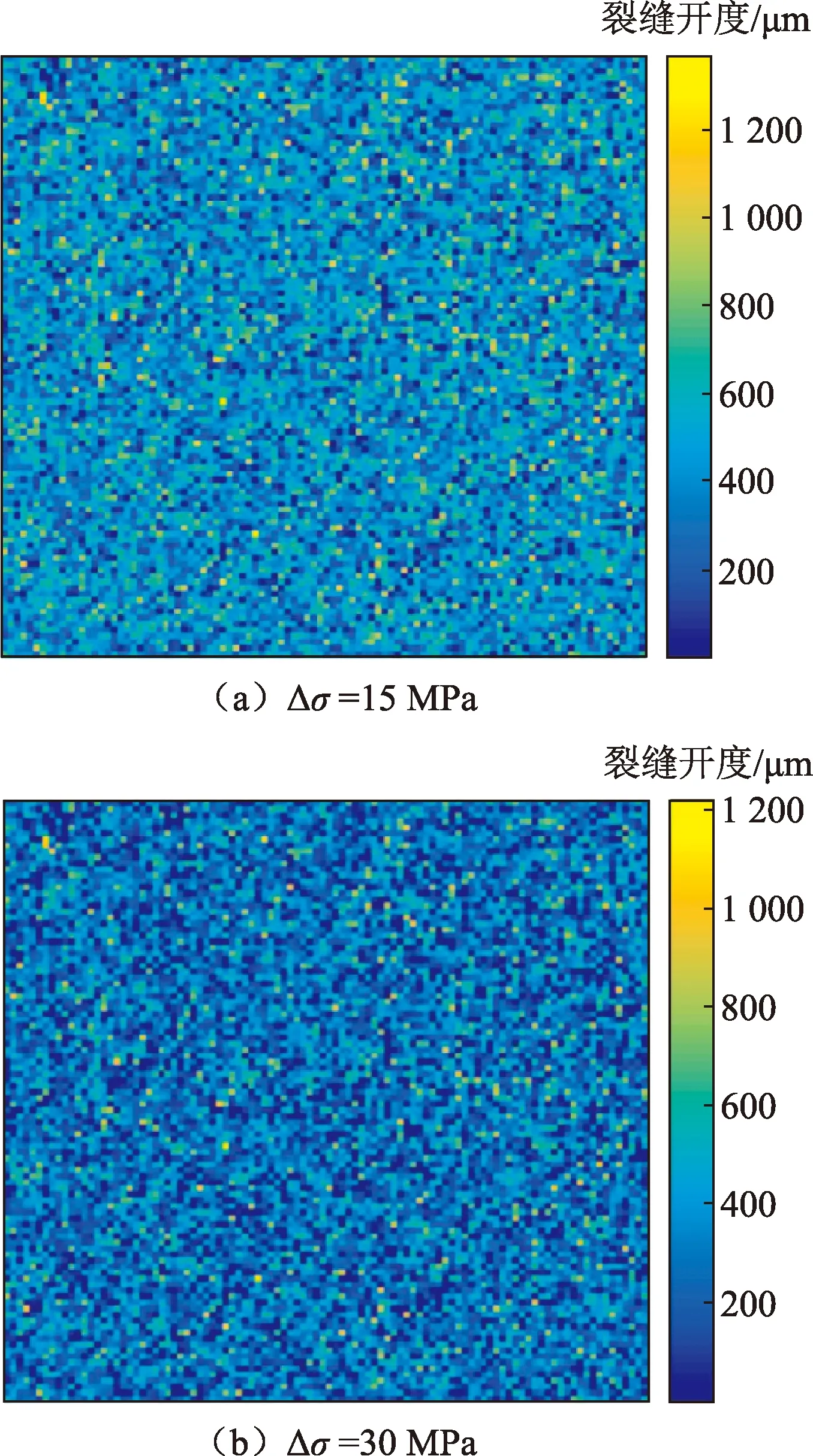
图8 不同有效应力条件下单条粗糙裂缝开度分布Fig.8 Local aperture distribution in single rough fracture under varying effective stress
3.2 有效应力对裂缝中毛管力及相对渗透率曲线的影响
图9为不同有效应力条件下的毛管力曲线和相对渗透率曲线。随有效应力的增加,毛管力曲线呈现整体抬升的趋势,其中平缓段由185 Pa增加到256和425 Pa,说明由于应力的增加,裂缝开度减小,驱替过程变得更加困难。实际生产过程中,油藏孔隙压力不断减小,导致有效应力增加。从图9可以看出,裂缝作为致密及页岩油藏的主要渗流通道,随有效应力不断增加,其中水相的相对渗透率基本不变,而油相的相对渗透率会明显减弱。
整体来看,有效应力由初始条件增加到15和30 MPa,裂缝的开度分别减小25.9%及51.7%,而油相的相对渗透率分别平均减小了10.7%和24.3%,裂缝所受有效应力越大,油相渗透率减小幅度越明显。这是因为裂缝表面的亲水性,导致水相主要占据相对较小的孔隙流动,受应力影响表现不明显,而油相主要在裂缝中较大开度的孔隙流动,随着有效应力增加,油相的流动通道明显被压缩,对应的毛管力显著增加,油相流动阻力增大,因此油相相对流动能力被削弱。另外,油驱水过程中,随有效应力的增加,油相开始流动时对应的含水饱和度和水相基本丧失流动能力所对应的含水饱和度均略有减小。这是因为油相普遍在较大孔隙中流动,应力的作用使流动通道明显变窄,驱替初始时,油相开始连续并流动所对应的含水饱和度越小,即随着生产的进行,裂缝所受到有效应力增大,油相越难以形成连续流动通道;同时,有效应力增加导致裂缝部分闭合,油相作为驱替相侵入连续的位置更加困难,当水相已基本无流动能力时,油相饱和度已达到较高水平,表现为相应的含水饱和度减小。相比于无法考虑应力变化对裂缝油水两相流动影响的光滑裂缝“X”型相渗模型[35-37],本文中提出的方法更能准确反映变应力条件下真实裂缝内部油水两相流动规律。
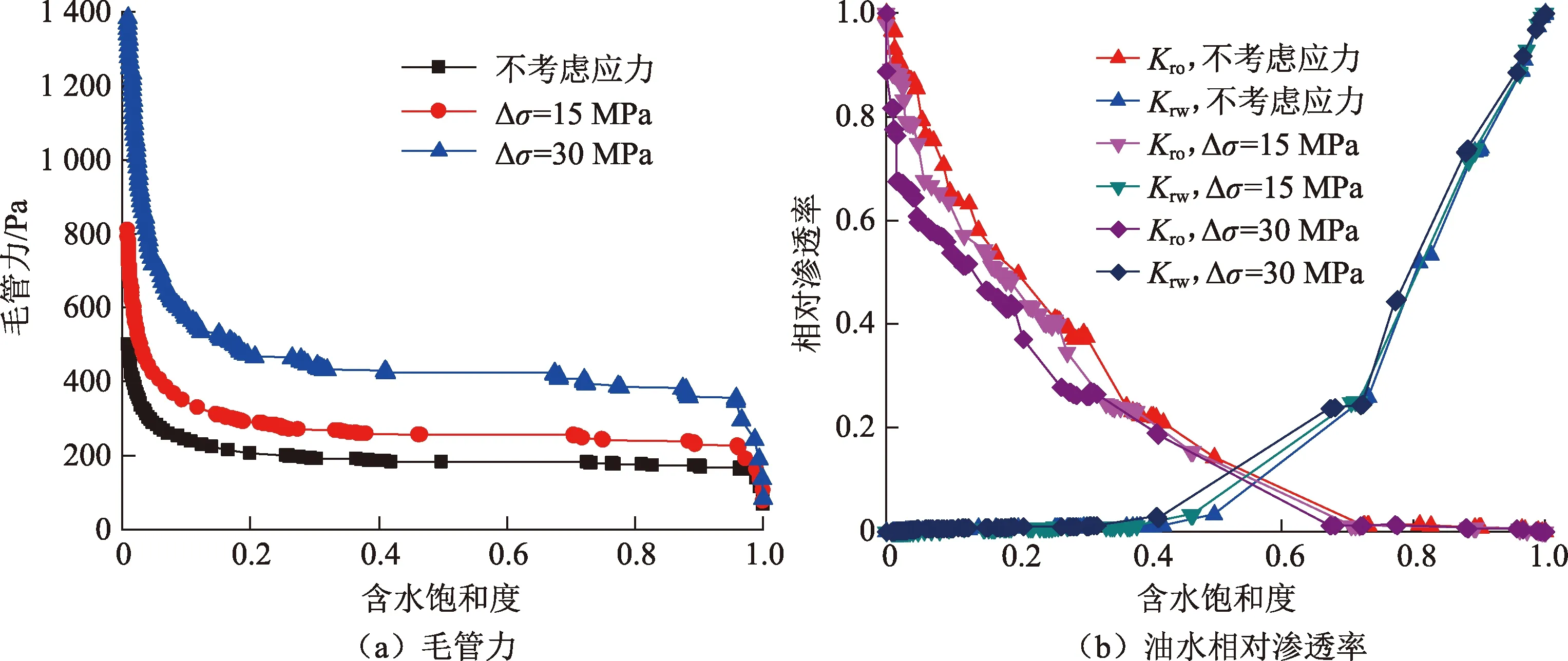
图9 不同有效应力条件下的毛管力及油水相对渗透率曲线Fig.9 Capillary pressure and relative permeability curves of oil and water under varying effective stress
4 结 论
(1)对于单条粗糙裂缝中油水两相流动,在初始含水饱和度降低阶段,油相流动能力极低,随着驱替过程的进行,油相流动占主导,水相基本失去流动能力。
(2)随着有效应力的增加,单条粗糙裂缝被压缩并出现局部闭合现象;裂缝毛管力曲线整体抬升;油相相对渗透率减小,且有效应力越大,油相相对渗透率减小越明显,而水相相对渗透率基本保持不变;同时,油相开始流动对应的含水饱和度和水相基本失去流动能力时对应的含水饱和度均随有效应力的增加而减小。
