基于K 近邻和粒子群优化的特征选择算法

钟昌康

（四川大学计算机学院，成都610065）

0 引言

在数据挖掘、机器学习、模式识别和信号处理等许多领域中，经常需要处理包含大量特征的数据集。在这种情况下，对数据进行降维预处理能大大提升学习算法的训练速度和性能。特征选择是数据降维领域中的重要方法。特征选择是从给定数据的原始特征集中选择特征子集的过程，通过特征选择算法选出的特征子集应该能尽量的表示原始特征集的特性。特征选择的重要性在于减小特征集合的大小并减少学习算法的搜索空间。在模式分类器的设计中，特征选择可以提高分类精度和并加快模型训练速度。

特征选择过程包含两个基本步骤：①评估特征或特征子集的优劣；②在特征空间搜索最优特征子集[1]。目前已经有许多基于统计学和数学特征的评估措施以及搜索技术用于特征选择领域。特征选择领域学者们已经开发了许多有效的特征选择算法，其中包括评估函数和搜索策略的各种组合。但是，统计方法的计算复杂度会随特征维度的增加而成指数增加。所以在现实应用中，统计方法不太适用。近年来，诸如人工神经网络、模糊集和粗糙集之类的软计算工具被广泛用于特征子集的评估，而遗传算法、粒子群优化等进化算法因为具有良好的全局搜索能力而被证明对于搜索最优特征子集的问题是有效的。

特征选择算法分为三种类型：①过滤器方法；②包装器方法；③嵌入式或混合方法。在滤波方法中，特征子集的优劣是通过某些基于数据集的指标来评估的，整个评估过程不涉及任何的学习算法。滤波方法往往需要较少的计算资源，但这种方法没有考虑特征对于最终的学习任务的影响，并且特征之间的相互作用可能会被忽视。包装器方法将学习算法的精度作为评估特征子集的指标。包装器方法选择与分类算法相关的特征，能得到更高的分类准确率，但是由于每次评估特征子集时都需要训练分类器，因此包装器方法的计算量通常很大。嵌入式特征选择算法嵌入在学习算法当中，当分类算法训练过程结束就可以得到特征子集。

在本文中，我们将K 近邻算法和粒子群算法结合，提出了一个基于K 近邻和离散粒子群优化的特征选择算法，K 近邻算法用于评估特征子集的优劣，拥有良好全局搜索能力的群体智能算法粒子群算法将用于在特征空间中搜索最优特征子集，本文所提算法在5 个UCI 数据上进行实验过后表明能有效降低数据维度并提高分类精度。

1 预备知识

1.1 粒子群优化算法

粒子群优化（Particle Swarm Optimization，PSO）算法[2]是Kennedy 和Eberhart 受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

在粒子群算法中，鸟被抽象为一个个的粒子，每一个粒子有自己的位置和速度，对于一个N 维优化问题，若粒子群的规模为M，则粒子i,( 0 ＜i ≤M )在N 维空间的位置表示为Xi=(x1,x2,x3,…,xN)，飞行速度表示为矢量Vi=( v1,v2,v3,…,vN)。每个粒子都有一个由目标函数决定的适应值，并且知道自己到目前为止发现的最好位置（pbest）和现在的位置Xi。这个可以看作是粒子自己的飞行经验。除此之外，每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置（gbest）（gbest 是pbest 中的最好值），这个可以看作是粒子同伴的经验。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动[6]。

粒子按照以下公式进行速度和位置的更新：

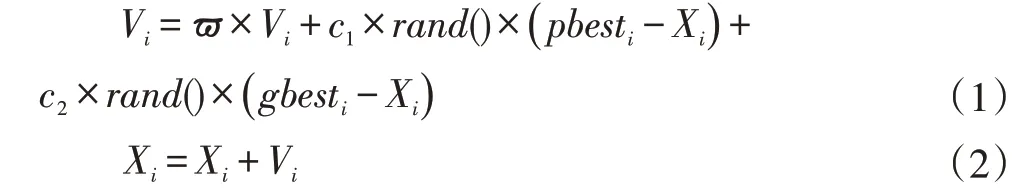
其中ϖ 叫做惯性因子，反映了粒子的运动习惯，代表粒子有维持自己先前速度的趋势，当ϖ 较大时，算法的全局搜索能力较强，局部搜索能力较弱[4]。当ϖ 较小时，算法的全局搜索能力较弱，局部搜索能力较强。其中c1 和c2 为学习因子，也称加速常数，代表了粒子向自己的最优经验学习和向所有粒子的最优学习的趋势，通过调整c1 和c2 可以平衡算法的探索和挖掘能力。第二部分为粒子的认知部分，反映了粒子对自身历史经验的记忆，代表粒子有向自身历史最佳位置逼近的趋势；第三部分为社会部分，反映了粒子间协同合作与知识共享的群体历史经验，代表粒子有向群体或邻域历史最佳位置逼近的趋势。rand（）是在0 到1 之间的两个随机数。

1.2 K近邻算法

K 近邻学习[3]是机器学习和数据挖掘领域中一种常见的监督学习方法，其工作机制非常简单。在给定训练样本后，基于某种度量找出训练集与测试集中最接近的K 个样本，即所谓的K 个邻居来预测样本类别。度量通常使用标准欧氏距离，其公式如下：

K 近邻的算法描述为：

（1）计算测试数据与各个训练数据之间的距离；

（2）按照距离的递增关系进行排序；

（3）选取距离最小的K 个点；

（4）确定前K 个点所在类别的出现频率；

（5）返回前K 个点中出现频率最高的类别作为测试数据的预测分类。

2 基于K近邻和粒子群优化的特征选择算法

我们可以将PSO 的思想用于最佳特征选择问题。考虑一个充满特征子集的大型特征空间。每个特征子集都可以看作是此类空间中的一个点或位置。如果数据集总共有N 个特征，则将有2N个特征子集，每个子集包含的特征数量和特征互不相同。最佳特征子集是特征数目最小，并且能使得基于该特征集训练出的分类器分类质量最高。现在我们将一个粒子群放入这个特征空间，每个粒子占据一个位置。粒子在此空间中飞行，它们的目标是飞行到最佳位置。随着时间的流逝，他们会改变自己的位置，彼此交流，并在本地最佳和群体最佳位置附近搜寻。最终，他们应该集中在良好的，也有可能是最佳的位置上。粒子群的这种探索能力可以使其具备执行特征选择和发现最佳特征子集的能力。由于特征选择是一个离散优化问题，所以在使用PSO 进行特征选择时，我们需要调整PSO 中的一些更新公式。

（1）粒子表示

我们将粒子的位置表示为长度为N 的0,1 向量，其中N 是特征的总数。每一位代表一个特征，值“1”表示选择了相应的特征，而“0”代表对应位置的特征没有被选择。每个粒子的位置都代表一个特征子集。初始化时，每个粒子的位置应该在（0,1）之间。

其中xi=1 代表第i 个特征被选择，否则代表第i个特征没有被选择。例如，X=(1,0,1,1,0)代表第一个、第三个、第四个特征被选择。

（2）位置更新

粒子按照如下公式进行位置更新：

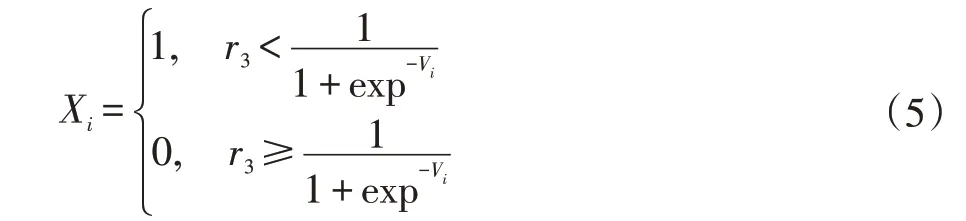
其中r3是属于（0,1）区间的一个随机数，当粒子的速度更新经过指数函数处理后，粒子的速度大小就位于（0,1）之间，然后通过生成随机数r3来决定粒子的下一步更新是变为1 还是0[5]。

（3）适应度函数

为了平衡分类精度和特征数目，我们将适应度函数定义为如下公式：

其中γR( D )在特征子集R 上训练出的分类器D 的分类精度，| R |是选择出来的特征子集包含的特征的数目，|C |是原始特征集合中特征总数。α 和β 是用来调节分类精度和特征数目两个目标函数比重的重要参数，α ∈( 0,1) 且β=1-α。

公式（4）代表分类质量和特征子集长度对于特征选择任务具有不同的意义。在本文的实验中，我们假设分类质量比子集长度更重要，并设置α=0.9，β=0.1，α 的值较大可以使得选出的特征子集能最大程度的代表原始特征集合。每个特征子集都通过这个适应度函数进行评估，适应度函数值越大代表特征子集越优。

算法整体流程如图1 所示。

3 实验

为了验证本文所提出的算法的优越性，我们从UCI 选取了5 个常用的数据集进行算法实验，表1 给出了这些数据集的简要概括信息。这些数据集的特征数目从9 到60 不等，而且这些数据集的样例数目也大小不一，从而能够很好地检验算法的在处理特征选择问题上的搜索能力。所有实验是在处理器为Intel Core i5-2320 3.00GHz 运行内存为6GB 的PC 上完成，最大迭代次数被设置为100，群体的数目被设置成10，惯性因子ω=0.5，c1=c2=2。适应度函数中的α和β被分别设置为0.99 和0.1。另外，所有统计结果是在独立运行30 次之后得到的，问题的维度和所对应数据集的特征数目是相等的。对于每个数据集，我们将其分为训练集和测试集，80%作为训练集，20%作为测试集。KNN（k=5）被用来作为分类器用来评估所选出的特征子集的好坏。

图1 算法整体框架

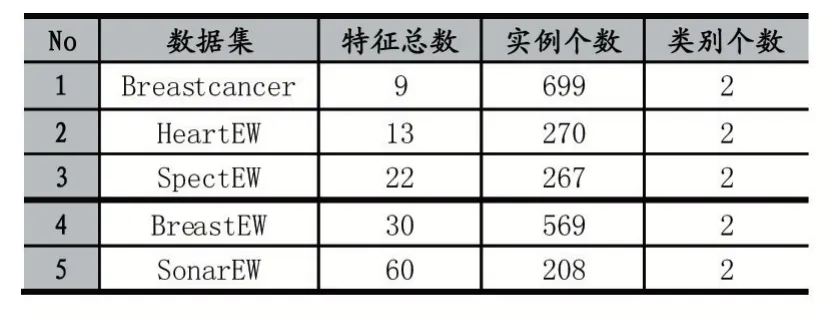
表1 使用数据集

从表2 的结果可以看出，通过使用PSO 对特征进行选择之后分类精度相比于使用全部特征训练的KNN有很大的提升，通过图2 我们可以看出特征选择并不意味着特征越少越好，从图2 的第三个小图我们可以看到，当算法在处理HeartEW 这个数据集的时候，最后选择的特征数目为9，而不是一开始算法就达到的5 个特征，这是因为适应度函数平衡了特征数目和分类精度两个目标，所以算法会在最终迭代结束时用较少的特征争取得到更高的分类精度。而且由图2 中的第一个小图我们可以看出，特征选择可以在减少特征的同时得到更高的分类精度，当算法在处理Breastcancer 这个数据集的时候，在第十九次迭代的时候，算法选择的特征由8 个降低到了7 个，但是分类器的准确率却从96.5%提升到了97.1%。综上所述，通过特征选择可以有效降低数据维度，提高算法性能。

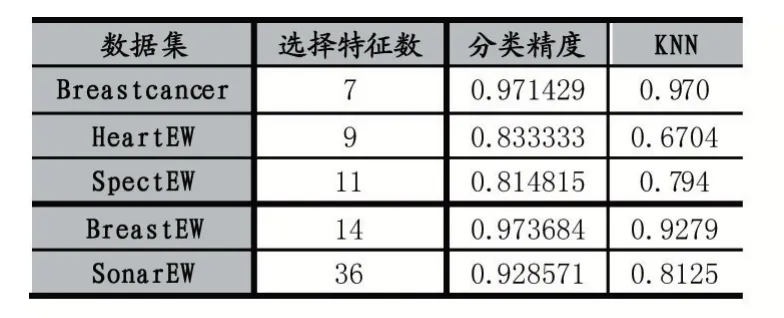
表2 实验结果

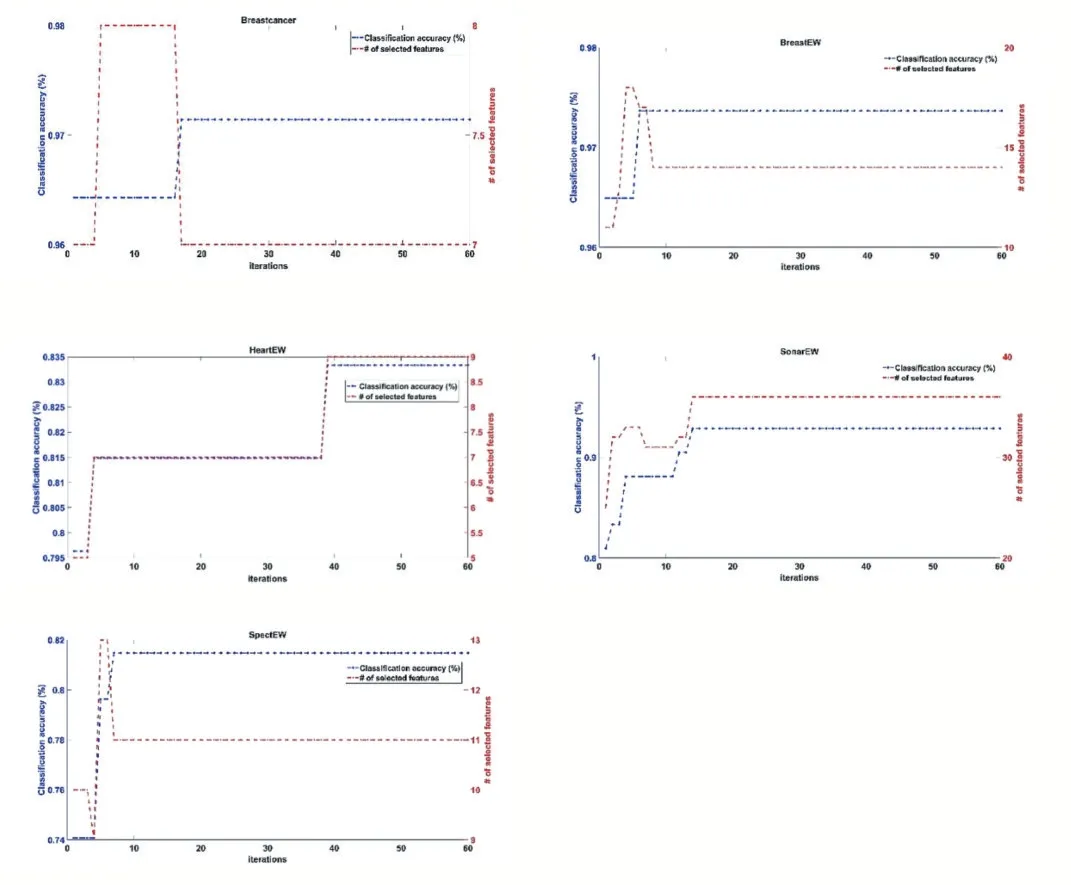
图2 基于K近邻和粒子群优化的特征选择算法的特征选择过程图

4 结语

在本文中，我们以粒子群优化为搜索算法，以K 近邻算法作为评估方法，提出了一种包装器式的特征选择方法，该方法以分类精度和特征子集的大小的综合评判作为评估函数，将两个目标函数统一在一个目标函数里。在将粒子群用于特征选择之前，需要一些离散化算法来离散化数据。我们在5 个UCI 基准数据集上的实验表明，该算法可以有效降低特征数量并提高分类器分类精度，与使用全部特征训练的K 近邻算法相比，分类准确率也有较大提升。未来工作可以使用更广泛的数据集检查算法的效率，使用不同的分类器对所选特征子集进行分类的准确性，采用不同的评估方法和搜索算法的组合。