一种针对EEG 伪迹的多窗卷积压制算法

孙望强，刘亮，郭庆功

（四川大学电子信息学院，成都610065）

0 引言

脑电信号的各种波形传达了具有临床价值的信息，对脑电信号的分析在神经科学、认知科学等领域都得到了广泛的应用[1-2]。测量脑电信号的过程中，脑电信号会受到电噪声等外部干扰和眼电、心电等生理伪迹信号的干扰[3-5]。眼电等伪迹干扰幅值会比脑电信号大10 倍之多，很大程度上会“淹没”神经信号[6-7]，因此脑电信号的信号SAR 很低，会使得对脑电信号的分析变得困难。

Nolan H.等人[8]基于统计特征对神经信号和伪迹干扰成分进行区分并有效删除伪迹成分，Petr Nejedly、Radüntz T 等人[9-10]将机器学习算法应用于脑电特征中实现伪迹的自动识别消除，Soomro MH[11]基于经验模式分解结合ICA 的算法用于眼电伪迹消除，并对比了伪迹前后脑电信号的SAR 和相关系数。但这些研究都未在少通道（如8 导）采集系统下进行分析，且都是通过粗删除的方式对判断为伪迹的成分进行处理。

在实际应用中，考虑脑电采集设备的成本问题，会选用8 导脑电信号采集设备。多通道采集系统测量的数据量较多，有效地区分脑电伪迹和神经信号之后删除伪成分可能不会导致神经信号泄露的问题，但在少通道采集系统（8 道）下，即使很好地判断出“伪迹”成分，这些成分中势必会含有一部分神经信号成分，如果通过粗删除的方式去除，会导致神经信号泄露的问题[12]。

为了解决这个问题，本文在Delpozo-Ba 等人[13]研究基础上，结合信号时、空特征，在局部化的时间片段上进行伪迹特征判别，对分类出的含有伪迹干扰较多的整导成分不进行粗删除处理，而是利用不同的窗函数优化组合并卷积压制伪迹特征，结果证明该算法可以消除眼电等伪迹且降低神经信号泄露的影响，提高处理之后脑电信号的SAR。

1 伪迹消除算法原理

1.1 ICA在伪迹消除算法中的应用

脑电信号分析中，最广泛使用的模型是假设被测的脑电信号是多个脑源与伪迹产生的电信号的线性组合，并瞬间传播到头皮区域[14-16]。可以用数学方程式（1）表示：

X=As+V （1）

其中X=[x(1 ),x( 2 ),…,x( N )]是一个n 行N 列的脑电信号数据矩阵，行n 表示测量的脑电信号的通道数（采集设备导数），列N 表示采样的数据点数；A 是一个n×n 的未知混合矩阵，V 代表外部噪声。ICA 的核心目标是估计解混矩阵W，得到观察信号的源成分，模型方程式如公式（2）所示：

S=WX （2）

其中S 是一个n×N 的未知源成分矩阵，由神经信号成分与伪迹成分组成。为了确保基本的ICA 模型能被估计，要做一些假设和约束：第一，源成分S 被假设是统计独立的；第二，源成分具有非高斯的分布；第三，假定混合矩阵A 是方阵，且可逆；第四，假定所有的混合变量X 与独立成分S 都是零均值；第五，观察信号X 必须可以白化。基于这些约束，利用ICA 解混观察信号X 得到源成分，并通过伪迹特定的统计特征、时间特征、空间特征等可将源成分S 分类成伪迹成分和神经信号成分。

1.2 实现代码多窗卷积组合优化的局部伪迹压制算法原理

步骤一，通过ADJUST[17]算法分离观察信号，并根据伪迹时、空特征分类得到干净成分。步骤二，将观察信号通过ICA 处理之后，在局部化时间片段上根据突发性电压定位伪迹特征，并利用窗函数，结合步骤一得到的干净成分插值压制局部伪迹。一方面在更精细的时间片段上处理，降低了伪迹的影响，另一方面保留了大量的有用的神经信号。流程如图1 所示。

眨眼等伪迹可以定位到相应的每一个时刻，表现为测量信号波形的突发性，可以用局部时刻突发性的电压来定位这些特征时刻。为了量化特征，首先通过ICA 分离观察信号得到的成分数据并对其求样本Z 分数，Z 分数是一种对原始数据的均值和方差进行标准化的常用统计数据分析方法。其定义如公式（3）所示：

这里X 表示数据，E(X)表示其期望值，σ(x)表示其标准差，其中X 表示ICA 分离之后的成分的每一个电压值和一阶导数值。这样就可以利用Z 分数来量化特征，表示为A[c,k]，标识第k 时刻成分c 的特征。

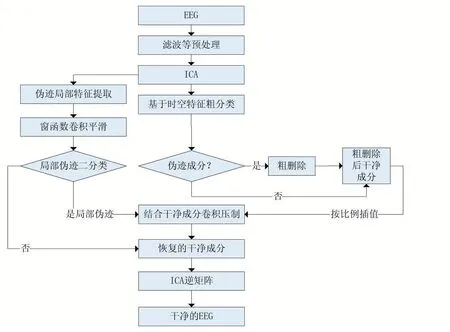
图1 算法流程图

由于一些小的脉冲干扰噪声可能会造成观察信号异常的数据点，可以用窗函数卷积运算来稳定所提取到的特征，更稳定的特征可以表示为B[c,k]，其定义如公式（4）：

这里A[c,k]表示由Z 分数量化的特征，*表示卷积运算，M 代表用于卷积的窗函数，L 表示整个的卷积范围，公式（4）的分母是一个归一化因子，它有效地在每一时刻将积分转换为加权平均，这样做可以抵消掉卷积的边缘效应。

公式（4）得到稳定特征之后，需要创建一个向量来标记第n 个时刻的成分c 的特征是不是属于伪迹。对每个时刻的某个成分的每一个特征设置一个阈值，设置阈值的目的是为了分类含有局部伪迹特征的成分和神经信号成分。为了更加方便与简洁，采用二分类阈值为p。其决策逻辑函数如公式（5）所示：

式（5）中自变量x 就是需要判断的特征，也就是由式（5）得到的稳定特征，这里需要传入的是max([B[c ,k-d],…,B[c,k+d]])，其中d 表示每个时间点附近需要的一个缓冲区域，使得这一区域内的特征被上面的逻辑函数f(x)分类为噪声。缓冲区域取0.09s 是验证为比较合适的，在这个0.09s 的区域会产生连续的噪声，可以与相邻的时刻很好的分离开。对每个成分每个时刻的特征B[c,k]用逻辑判断之后，用F[c,k]表示，F[c,k] 的值用1 和0 分别表示这个特征是否是伪迹。

经过式（5）处理之后，需要对那些被标注为1 的特征时间段进行处理，不直接删除这些时间片段，而是通过步骤一获得的干净成分按比例插值处理，也就是按照逻辑函数F[c,k]来混合两种成分。其中控制混合两种成分的信号为Y[c,k]，定义如公式（6）所示：

其中M1 是长度为N 的窗函数，用于对检测区域的边缘进行调整，从而平滑混合中的过渡，最后得到干净的成分R[c,k]。

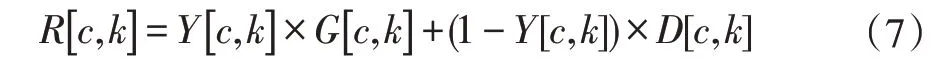
Y[ c,k] 是由式（7）得到的控制信号，G[ c,k] 是基于时、空特征得到的相对干净的成分，D[ c,k] 是由观察信号盲源分离得到的成分，最后混合G[ c,k] 和D[c ,k] 得到保留更多有用信号的干净成分R[c ,k] ，这样得到的结果不仅减少了神经信号的泄露，而且成功地压制了伪迹。

2 实验结果分析

本文脑电信号采集系统是ANT-NEURO EEG/ERP系统，给被试人员分别采用8 电极、32 电极采集被试脑电信号。其中A/D 采样频率设置为1000Hz，头皮阻抗小于5KΩ，受试者在头脑清醒的情况下接受“怪球”实验。对采集的脑电数据利用EEGLAB、MNE-Python 联合进行算法编程与分析，8 电极、32 电极图分别如图2、图3 所示。

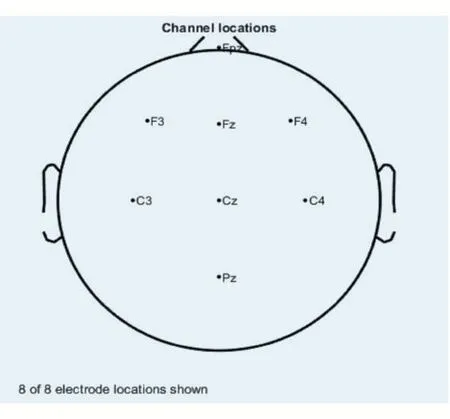
图2 8道电极图

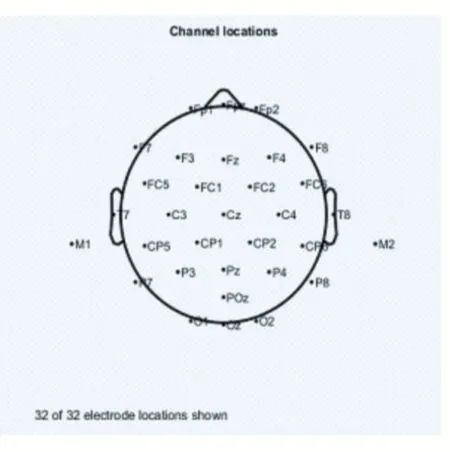
图3 32 道电极图

其中FPz、Fz、Cz、Pz、Oz 等分别表示脑的前额区域、额区、中央区、顶区和枕区，8 电极采集系统采用“平均”参考电极，32 道采集系统采用M1、M2 为参考电极，在分析时以刺激呈现200ms 为基线，每一个epcoh分析时程是-200ms 到800ms。

首先将采集信号用FIR 滤波器进行1hz-30Hz 的滤波，随后进行基线校准和分段处理，可以得到图4（8电极），图5（32 电极）的观察信号波形。

图4 经过分段处理后的8道观察信号

图5 经过分段处理后的32道观察信号

图4、图5 中可以很明显地看到眼电等伪迹干扰，需要压制这些伪迹造成的干扰。首先是要获得观察信号的源成分，因此我们采用ICA 算法对图4、图5 中的观察信号进行盲源分离，分别得到8 导、32 导时间波形成分图6、图7 所示。

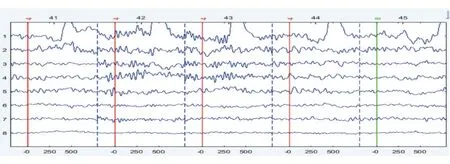
图6 8电极源成分时间波形图

图7 32电极源成分时间波形图

利用ADJUST[17]算法，基于时空特征，可以得到相对干净的成分，但会造成神经信号泄露。当得到相对干净的成分之后，结合最优的多窗卷积压制算法，将相对干净的成分按比例局部插值到伪迹成分以达到压制伪迹的目的，这样做不仅能得到更加干净的神经信号成分，而且能保留更多的神经信号，实现伪迹噪声降低和神经信号泄漏之间的均衡。利用多窗卷积压制算法得到的脑源成分（8、32）如图8、9 所示，对比图6、图7发现大部分伪迹成分已经被成功压制。

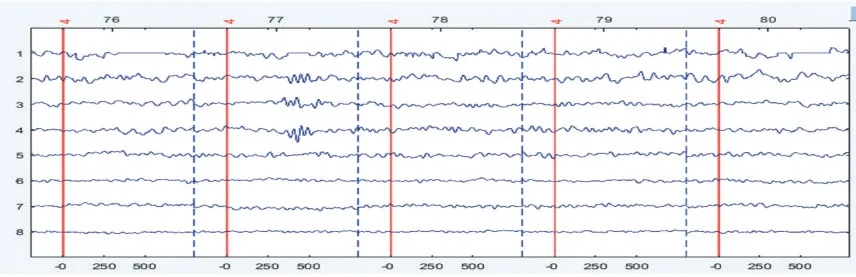
图8 处理之后8电极干净源成分

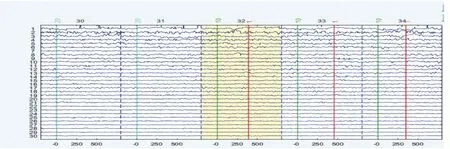
图9 处理之后32电极干净源成分

最后利用混合矩阵可恢复观察信号，如图10、图11 所示。

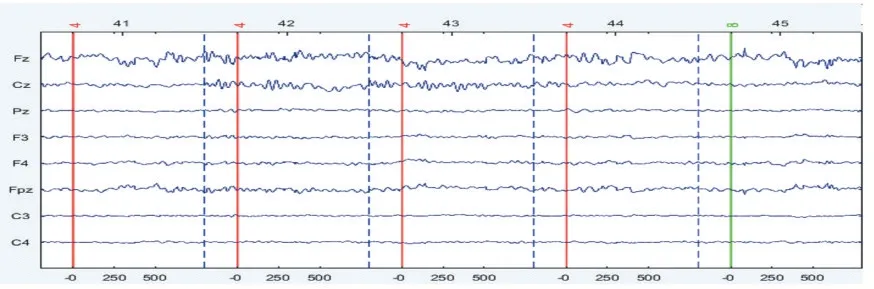
图10 恢复的8电极观察信号

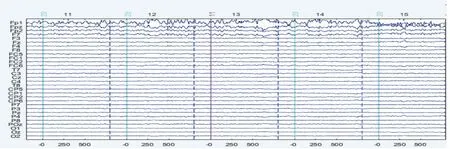
图11 恢复的32电极观察信号

对比图4、图5 得到的观察信号，可以看到图10、图11 中眨眼等伪迹干扰已经成功被压制。由以上分析可得，利用本文算法处理之后，所采集的脑电信号的伪迹干扰确实成功被压制。为了进一步量化算法去噪效果，采用SAR（噪声伪迹比）衡量，其定义如公式（8）所示。

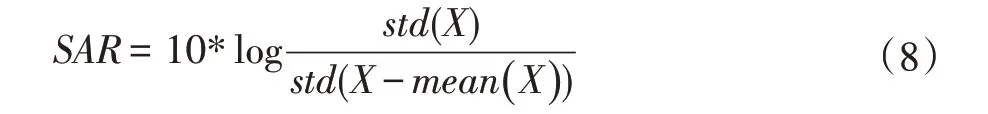
其中mean 代表求数据的均值，X 代表原始未校正的EEG 信号。SAR 体现了消除伪迹的效果，8 电极、32电极SNR 结果分别如表1、表2 所示。

表1 8 电极采集系统SAR 对比表

表2 32 电极采集系统SAR 对比表

3 结语

在本文中，基于脑电信号时、空特征和窗函数卷积组合优化的方式来对局部伪迹进行压制。在8、32 电极采集系统下，未处理脑电信号SAR 分别是-19.765dB，-19.616dB，通过本文提出的方法处理后脑电信号的SAR 分别是2.832dB，2.743dB，且在8 电极采集系统下效果较FastICA、EMD-ICA 处理后的SAR 有明显提高。实验结果表明该算法不仅能够压制眨眼伪迹干扰，还能较好地保留神经信号的成分，实现了伪迹噪声降低和神经信号泄露之间的均衡。